Focused Electric Field
In the plane, there is a parabola described by . The parabola has a uniform linear charge density .
The magnitude of the electric field at the focus of the parabola can be expressed as , where is the Coulomb constant and and are coprime positive integers .
Determine .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
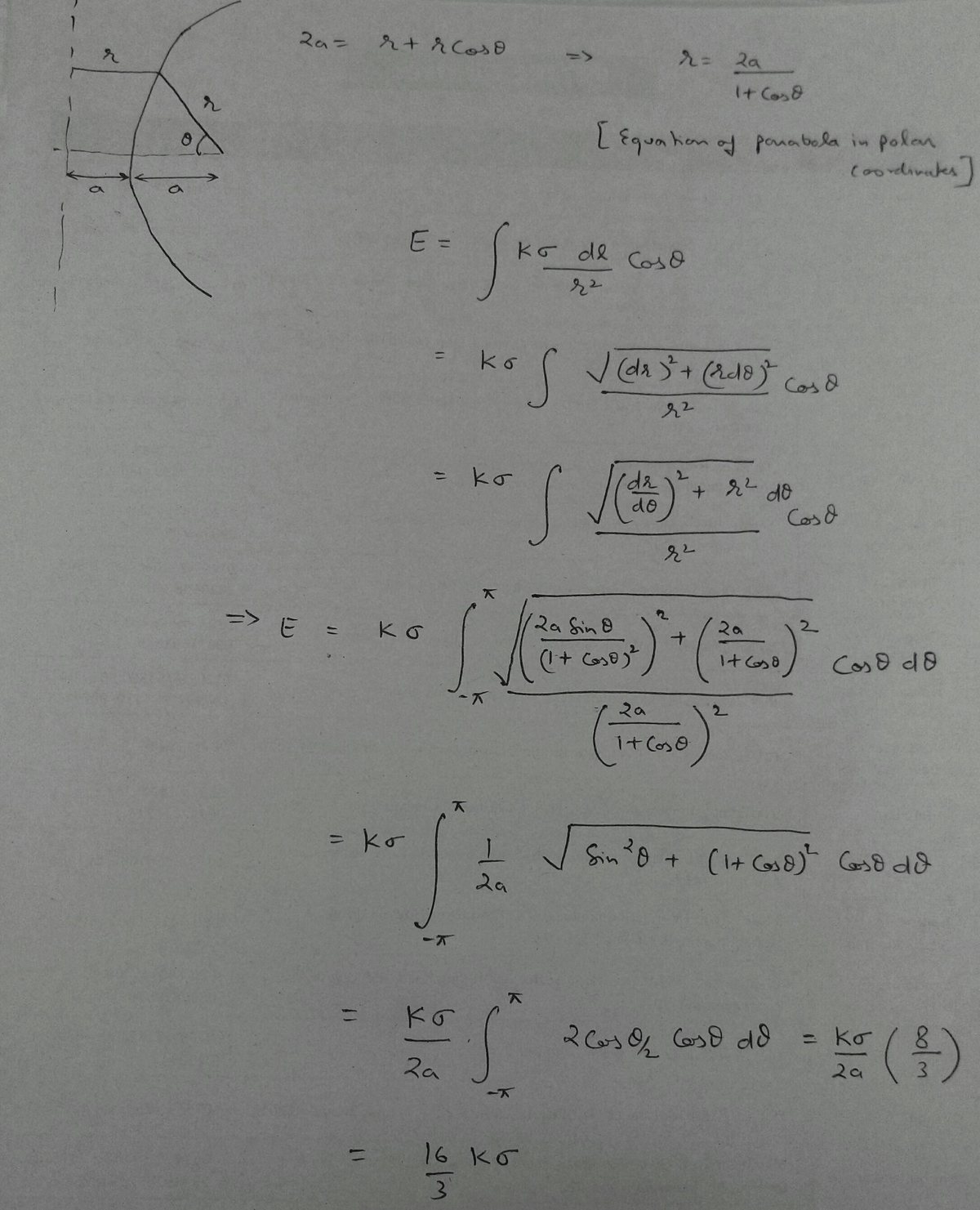
Recall that d E y = r 2 k d q cos θ .
So, what's left to do is to prove that ∫ 0 ∞ [ x 2 + ( 4 1 − x 2 ) 2 ] 3 / 2 1 + 4 x 2 ( 4 1 − x 2 ) d x = 3 8 .
Note that we can simplify the denominator of the integrand to
[ x 2 + ( 4 1 − x 2 ) 2 ] 3 / 2 = [ x 2 + x 4 + 1 6 1 − 2 1 x 2 ] 3 / 2 = [ x 4 + 1 6 1 + 2 1 x 2 ] 3 / 2 = [ ( x 2 + 4 1 ) 2 ] 3 / 2 = ( x 2 + 4 1 ) 3
We start by making the trigonometric substitution x = 2 1 tan y , then d y d x = 2 1 sec 2 y ,
∫ 0 ∞ [ x 2 + ( 4 1 − x 2 ) 2 ] 3 / 2 1 + 4 x 2 ( 4 1 − x 2 ) d x = = = = = = = ∫ 0 ∞ ( x 2 + 4 1 ) 3 1 + 4 x 2 ( 4 1 − x 2 ) d x ∫ 0 π / 2 ( 4 1 ) 3 ( 1 + tan 2 y ) 3 1 + tan 2 y ⋅ 4 1 ( 1 − tan 2 y ) ⋅ 2 1 sec 2 y d y 8 ∫ 0 π / 2 ( sec 2 y ) 3 sec y ( 1 − tan 2 y ) ⋅ sec 2 y d y 8 ∫ 0 π / 2 sec 3 y 1 − tan 2 y d y 8 ∫ 0 π / 2 cos y ( 1 − 2 sin 2 y ) d y , let y = sin y ⇒ d y = cos z d z 8 ∫ 0 1 ( 1 − 2 z 2 ) d z 8 [ z − 3 2 z 3 ] 0 1 = 3 8 .
And we're done!