Folding Polyhedra
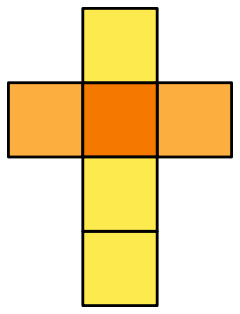A net of a cube
In geometry, a
net
of a polyhedron is an unfolding of the surface of the polyhedron produced by cutting the solid along some of its edges and flattening it into a polygon in the plane.
Many different nets can exist for a given polyhedron, depending on the choices of which edges are joined and which are separated. See this problem . Conversely, may a given net fold into more than one different polyhedron?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Imagine a cube, but replace one of its faces with the lateral faces of a square pyramid whose base would have been the deleted face. For a given pyramid height, the apex of the pyramid could be positioned either on the inside or the outside of the deleted cube face, yielding two different polyhedra that share the same set of nets.