For all n >=3
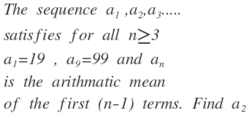 Also try
No. of solutions
Also try
No. of solutions
The series is not specifically A.P
The answer is 179.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Parth Lohomi since you have been taking the questions from various good books. So I think you should try and mention the source of the problem because if the question is from a book then the credit of the question should be given to the book not to you.
a 3 = a 4 = a 5 . . . . . . . . . . . . . . . . . . = a 9 = 2 1 9 + a 2 By this a 2 = 1 7 9 . @brian charlesworth nice solution.
And how this problem got on to level 5!!!!.
Log in to reply
Thanks. Yes, I would put this question at level 3; I've seen some level 3 questions that really should be at level 5, but for the most part the algorithm that determines the levels works reasonably well.
Log in to reply
@brian charlesworth This question is highly rated because ,the main part was that not taking it as an A.P.If you take it as A.P then your answer gets incorrect! Okay now it will be clear how this question reached on level 5 ,
Log in to reply
@Parth Lohomi – I would still rate this problem as level 3
@Parth Lohomi – Fair enough. It's a good question, anyway, whatever the level. :)
Let S n = a 1 + a 2 + a 3 + . . . + a n , then a n = n − 1 S n − 1 for n ≥ 3 .
Now a 3 = 2 S 2 = 2 a 1 + a 2 ⇒ a 1 + a 2 = 2 a 3 ⇒ S 3 = a 1 + a 2 + a 3 = 3 a 3
a 4 = 3 S 3 = 3 3 a 3 = a 3 ⇒ S 4 = S 3 + a 4 = 3 a 3 + a 3 = 4 a 3
Similarly, a 5 = a 3 and S 5 = 5 a 3 . . . ⇒ a n = a 3 for n ≥ 3
⇒ a 3 = a 9 = 9 9 ⇒ a 3 = 2 a 1 + a 2 = 2 1 9 + a 2 = 9 9 ⇒ a 2 = 1 7 9
I will first prove that a n = a 3 for n ≥ 3 using induction.
Clearly a 3 = a 3 , establishing the base case.
Now assume that a k = a 3 for some k ≥ 3 .
We have that a k + 1 = k a 1 + a 2 + . . . . + a k − 1 + a k , ( A ) .
But a k = k − 1 a 1 + a 2 + . . . + a k − 1 , and thus
a 1 + a 2 + . . . . + a k − 1 = ( k − 1 ) a k .
Substituting this result into equation ( A ) we see that
a k + 1 = k ( k − 1 ) a k + a k = a k ,
and so by the induction hypothesis a k + 1 = a 3 , thus completing the proof by induction.
Thus a 3 = a 9 = 9 9 . But a 3 = 2 a 1 + a 2 , so
9 9 = 2 1 9 + a 2 ⟹ a 2 = 2 ∗ 9 9 − 1 9 = 1 7 9 .