Force between perpendicular rods

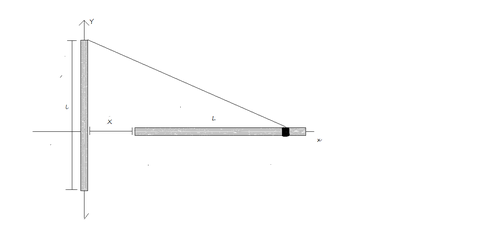Classical Mechanics Level pending

A variation of this problem . An electrostatic force of interaction is felt by two perpendicular rods each of length $L=$ and at distance of $x$ as shown in the figure above.

Then what is the electrostatic force of interaction when:

$L=x?$

$\lambda =1\mu c/m\quad K=9\times { 10 }^{ 9 }{ N }{ m }^{ 2 }/{ c }^{ 2 }$

The length of the rods isn't necessary.

The answer is 0.0042.

1 solution

Beakal Tiliksew
Apr 30, 2014

By symmetry we are left with only the $x$ component of the force. That is

$d{ q }_{ x }=\lambda dx,\quad \quad d{ q }_{ y }=\lambda dy\quad$

$d{ F }_{ x }=\frac { Kd{ { q } }_{ x }d{ q }_{ y } }{ { r }^{ 2 } } cos\theta =\frac { K{ \lambda }^{ 2 }(2L-x)dxdy }{ { \left[ { \left( 2L-x \right) }^{ 2 }+{ y }^{ 2 } \right] }^{ 3/2 } } \\ { F }_{ x }=\int _{ -L/2 }^{ L/2 }{ dy } \int _{ 0 }^{ L }{ \frac { K{ \lambda }^{ 2 }(2L-x)dx }{ { \left[ { \left( 2L-x \right) }^{ 2 }+{ y }^{ 2 } \right] }^{ 3/2 } } }$

The double integral can be calculated giving

${ F }_{ x }=K{ \lambda }^{ 2 }ln\left( \frac { -1 }{ 16 } (3+\sqrt { 5 } )(\sqrt { 17 } -9) \right)$

As You can see the length is not necessary.

Hi, I guess you have given wrong answer to the problem. The correct answer should be $0.420742$ . The expression you gave at last gives this answer.

Also, if you know the electric field on a point on axis of a rod, you can do it easily. I directly formed this single integral:

$2k \lambda^2 l \displaystyle \int_{l}^{2l} \dfrac{dr}{r \sqrt{4r^2+l^2}}$

jatin yadav - 7 years, 1 month ago

Could you check your final answer one last time.

Beakal Tiliksew - 7 years, 1 month ago

Answer is 0.420742 for sure. Even $k \lambda^2 \ln \bigg( \dfrac{-1}{16} (3+\sqrt{5})(\sqrt{17}-9)\bigg)$ = 0.420742.

Are you taking $\lambda = 1 \mu C/m$ , rather than $\lambda = 10 \mu C /m$

jatin yadav - 7 years, 1 month ago

And I knew that the double integral could have been left, I wanted it to be more general

Beakal Tiliksew - 7 years, 1 month ago

@Beakal Tiliksew – Even in the single integral form, it is completely general.

jatin yadav - 7 years, 1 month ago

@Jatin Yadav – oops, sorry again, damn I am pron to making mistakes. I can't change the answer, so that you could get it right.

And what I meant by general was if you didn't know the electrostatic force between a rod and a point charge, just like starting from charge

Beakal Tiliksew - 7 years, 1 month ago

Force between perpendicular rods

The answer is 0.0042.

1 solution

0 pending reports