Force machine pushes cart
Consider the following situation, where a cart of mass 5 0 k g is given a push by a 'force machine'. It exerts a 1 k N force over a period of 0 . 1 s on the cart. The track between A and B is frictionless, while the track between B and C has a coefficient of friction of μ .
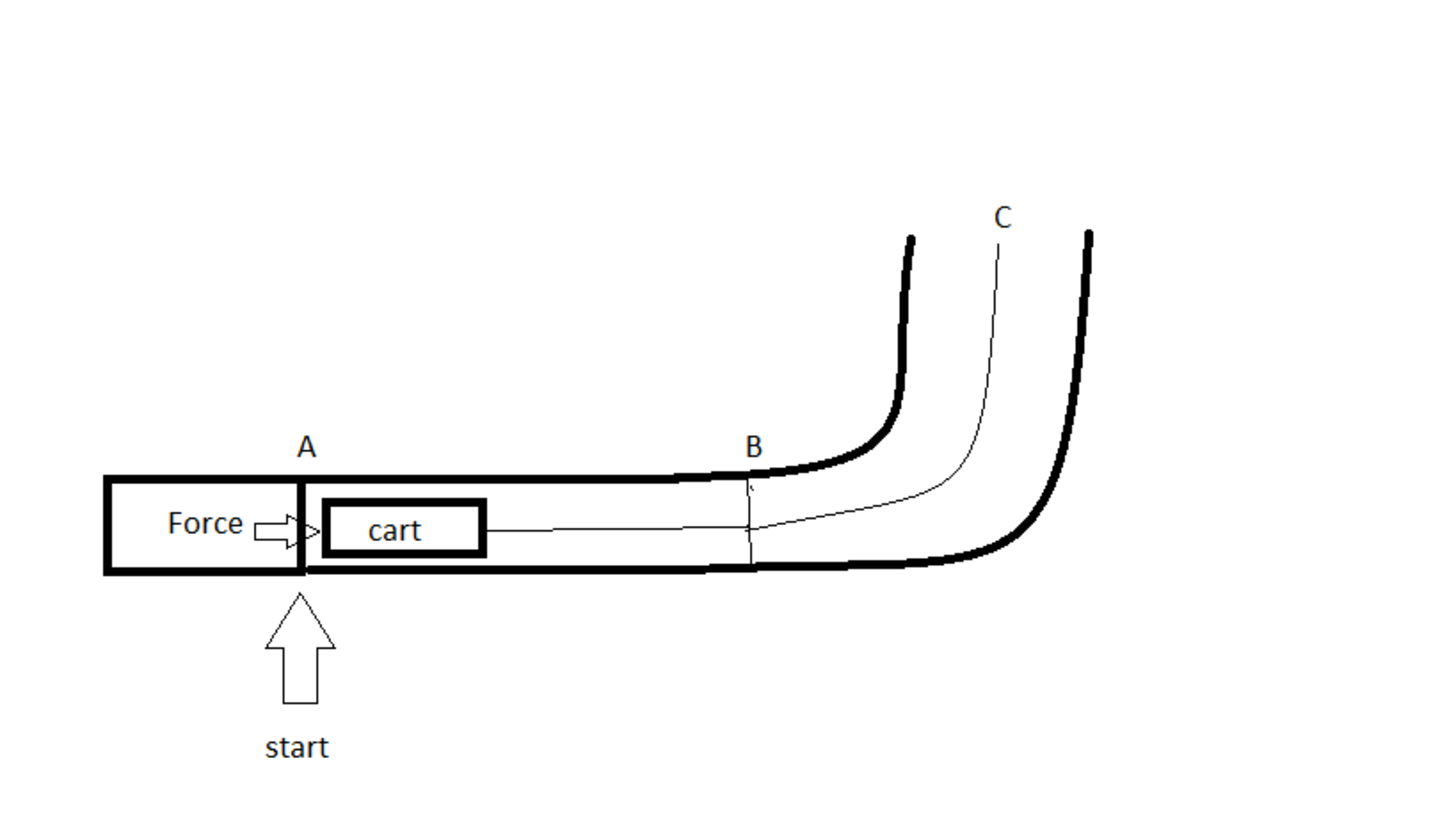
If the cart stops when its horizontal distance from B is 1 m , find μ . It can be expressed as μ = g ( b + ln ( a + b ) ) b 2 Enter a + b .
Details and Assumptions:
- g Is the downward acceleration due to gravity: g = 9 . 8 1 m s − 2 .
- Assume that the cart is symmetrical so its center of mass is the center of the rectangle depicting the cart.
- The cart is at rest prior to being pushed by the force machine.
- The cart follows the track perfectly and doesn't bump into the sides of the track.
- The path, shown as the thin line, is modelled by the equation y = 2 x 2 between B and C.
- The diagram is just a rough sketch; not to scale.
- The picture is a top view of the situation. That is, the acceleration due to gravity goes into the page.
Edit: Since my solution did not take into account the forces required to keep the cart on its path, just ignore these forces. This means that the only unbalanced force acting on the cart from B to C is the friction force directly opposing its motion.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I think that your solution is incomplete. If the particle follows a predefined path, the only force acting on it cannot just be friction. There has to be an additional constraint force that keeps the particle confined to the path y = x 2 / 2 .
Log in to reply
true. Does it affect the answer though?
Log in to reply
Oh, yes, absolutely. When you rigorously derive the equations of motion along the curve, the expression for friction coefficient is no longer the one that you have derived. It is in fact governed by a cubic equation as is seen in the solution that I have posted.
Moreover, another flaw in your solution is that you have assumed a constant acceleration magnitude over the path length. How do you know that this is indeed the case?
Log in to reply
@Karan Chatrath – Maybe I should delete this problem?
Log in to reply
@Charley Shi – I think that you should. Try attempting this problem when you can:
https://brilliant.org/problems/wire-reaction-force
But I really liked this problem, though. You could re-do it for yourself and repost another version of it
Log in to reply
@Karan Chatrath – thanks! To be honest, I should probably stick with electrical stuff lol
Log in to reply
@Charley Shi – Well, electromagnetism problems are out of my comfort zone, but I have still posted some exercises on it, which have also been reported. I would encourage you to keep posting on anything you enjoy.
Yea it does effect
I see that this problem is marked as popular. Probably because it was not reported. I suggest you edit the answer instead of reposting it.
Log in to reply
I actually don't understand the stuff that gets involved once you account for the constraint force. (it's outside my level) I just added an extra assumption at the end of the question.
Log in to reply
Let me draw an analogy: If a particle slides down an inclined plane, it naturally experiences a reaction force from the surface of the plane. If that reaction force becomes zero, then the particle loses contact.
A similar argument applies here, so this is elementary and not beyond a certian level as you say. Let us say that you ignore the constraint force and only account for friction. Writing out the equations of motion as per Newton's law (try this yourself) leads to:
m x ¨ = − f cos θ m y ¨ = − f sin θ tan θ = d x d y y ¨ = x x ¨ + x ˙ 2 f = μ m g
So by looking at the equations above, one can see that there are two different differential equations governing the time evolution of x , which is obviously wrong. So accounting for the constraint force is critical otherwise the physics of the situation is incorrect.
Log in to reply
@Karan Chatrath – I intended the track from the top view to be modelled by y = 2 x 2 . So the track is level but it is curved between B and C.
Log in to reply
@Charley Shi – The inclined plane point that I was making was an analogy. I do understand your explanation of the problem.
@Charley Shi – I have edited my earlier comment. I hope it makes sense now.
Log in to reply
@Karan Chatrath – Thanks! I'll see if I can get my head around this lol
Log in to reply
@Charley Shi – Plus, your solution does not explain why the acceleration is of a constant magnitude. It is an assumption and an unsubstantiated one.
I'll try one last time: The point I am trying to make is that your solution to this problem is an incorrect application of the laws of motion. The laws of motion applied to this system must not yield redundant differential equations governing the time evolution of x . Here you can clearly see (from my earlier comment) that only accounting for friction gives two different equations for x ¨ which is wrong. There must be a unique differential equation for x ¨ that fully describes the cart's motion along the curve.
Following the push the force machine gives, the cart gains momentum Δ p = m Δ v = F Δ t . Using the values in the question statement, we can calculate the initial velocity. v i = m F Δ t = 5 0 1 0 0 0 × 0 . 1 = 2 m s − 1 The only unbalanced force acting on the cart between B and C is the frictional force. This force is in the opposite direction of the motion of the cart. Since the acceleration due to this force is parallel to the cart's motion, we can use the kinematic equation v f 2 = v i 2 + 2 a s to solve for the acceleration. We already know that v f = 0 m s − 1 and v i = 2 m s − 1 , but we don't know s yet. To calculate s , find the total length of the track between B = ( 0 , 0 ) and C = ( 1 , 2 1 ) using the arc length formula. s = ∫ x = 0 1 1 + ( d x d y ) 2 d x = ∫ x = 0 1 1 + x 2 d x This integral can be solved using a trigonometric substitution of x = tan θ , so d x = sec 2 θ d θ . s = ∫ θ = arctan ( 0 ) arctan ( 1 ) 1 + tan 2 θ sec 2 θ d θ = ∫ θ = 0 4 π sec 3 θ d θ
This can be solved using integration by parts, yielding s = 2 2 + ln ( 1 + 2 ) Using this, a = 2 s v f 2 − v i 2 = 2 + ln ( 1 + 2 ) 0 2 − 2 2 = 2 + ln ( 1 + 2 ) − 4 This is negative, which makes sense because the acceleration is in the opposite direction to motion. The friction force is f = m a = μ N where N is the normal force N = m g . Thus, μ = N m a = m g m a = g a = g ( 2 + ln ( 1 + 2 ) ) 4 The acceleration is taken as positive because the coefficient of friction must be positive. a + b = 1 + 2 = 3