Force on Sub-Region

Classical Mechanics Level 5

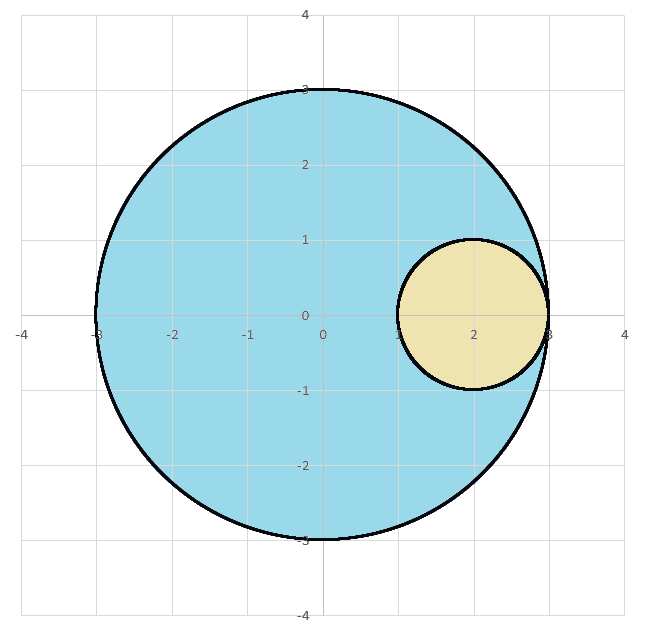
A uniform, solid sphere of radius 3 3 has its center on the origin in the x y z xyz coordinate system. The sphere has 1 1 unit of mass per unit volume.

Consider a sub-region within the greater sphere. The sub-region is a sphere with radius 1 1 centered at ( x , y , z ) = ( 2 , 0 , 0 ) (x,y,z) = (2,0,0) .

What is the magnitude of the net gravitational force on the mass within the sub-region?

Note: Universal gravitational constant G = 1 G = 1 , for simplicity

Hint: I used a triple integral to solve this. It might also be possible to do this with a sextuple integral, but that is much more demanding (and there is a risk of singularities arising at the sub-region boundary). The triple integral avoids the singularities too.


The answer is 35.0.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mark Hennings
Jun 27, 2019

The force F \mathbf{F} on the subregion due to the larger region is equal and opposite to the force on the larger region due to the subregion. Since the subregion is spherically symmetric, the gravitational field outside the subregion due to that subregion is equal to that of a point particle of the same mass m m as the subregion at the centre of the subregion. This force clearly acts parallel to the x x -axis, and so F \mathbf{F} has magnitude ∣ F ∣ = ∭ x 2 + y 2 + z 2 ≤ 9 ( x − 2 ) 2 + y 2 + z 2 ≥ 1 G m ρ ( x − 2 ) 2 + y 2 + z 2 × 2 − x ( x − 2 ) 2 + y 2 + z 2 d x d y d z |\mathbf{F}| \; = \; \iiint_{{x^2 + y^2 + z^2 \le 9} \atop {(x-2)^2 + y^2 + z^2\ge 1}} \frac{Gm\rho}{(x-2)^2 + y^2 + z^2} \times \frac{2-x}{\sqrt{(x-2)^2 + y^2 + z^2}}\,dx\,dy\,dz We are integrating over a volume of revolution, and we have G = ρ = 1 G=\rho=1 and m = 4 3 π m=\tfrac43\pi , so that ∣ F ∣ = 4 3 π ∬ x 2 + y 2 ≤ 9 , y ≥ 0 ( x − 2 ) 2 + y 2 ≥ 1 2 π y ( 2 − x ) ( ( x − 2 ) 2 + y 2 ) 3 2 d x d y |\mathbf{F}| \; = \; \tfrac43\pi \iint_{{x^2 + y^2 \le 9\,,\,y \ge 0} \atop {(x-2)^2 + y^2 \ge 1}} \frac{2\pi y(2-x)}{((x-2)^2+y^2)^{\frac32}}\,dx\,dy But then ∣ F ∣ = 8 3 π 2 ∫ − 3 1 ( ∫ 0 9 − x 2 y ( 2 − x ) ( ( x − 2 ) 2 + y 2 ) 3 2 d y ) d x + 8 3 π 2 ∫ 1 3 ( ∫ 1 − ( x − 2 ) 2 9 − x 2 y ( 2 − x ) ( ( x − 2 ) 2 + y 2 ) 3 2 d y ) d x = 8 3 π 2 ∫ − 3 1 [ − 2 − x ( x − 2 ) 2 + y 2 ] y = 0 9 − x 2 d x + 8 3 π 2 ∫ 1 1 [ − 2 − x ( x − 2 ) 2 + y 2 ] y = 1 − ( x − 2 ) 2 9 − x 2 d x = 8 3 π 2 ∫ − 3 1 { − 2 − x 13 − 4 x + 1 } d x + 8 3 π 2 ∫ 1 1 { − 2 − x 13 − 4 x + 2 − x } d x = 32 3 π 2 − 8 3 π 2 ∫ − 3 3 2 − x 13 − 4 x d x = 32 3 π 2 − 2 3 π 2 ∫ − 3 3 { 13 − 4 x − 5 13 − 4 x } d x = 32 3 π 2 − 2 3 π 2 [ − 1 6 ( 13 − 4 x ) 3 2 + 5 2 13 − 4 x ] − 3 3 = 32 3 π 2 − 2 3 π 2 ( − 1 6 + 5 2 + 125 6 − 25 2 ) = 32 9 π 2 \begin{aligned} |\mathbf{F}| & = \; \tfrac83\pi^2\int_{-3}^1\left( \int_0^{\sqrt{9-x^2}}\frac{y(2-x)}{((x-2)^2+y^2)^{\frac32}}\,dy\right)dx + \tfrac83\pi^2\int_1^3\left(\int_{\sqrt{1-(x-2)^2}}^{\sqrt{9-x^2}} \frac{y(2-x)}{((x-2)^2+y^2)^{\frac32}}\,dy\right)\,dx \\ & = \; \tfrac83\pi^2 \int_{-3}^1 \left[-\frac{2-x}{\sqrt{(x-2)^2+y^2}}\right]_{y=0}^{\sqrt{9-x^2}}\,dx + \tfrac83\pi^2\int_1^1\left[-\frac{2-x}{\sqrt{(x-2)^2+y^2}}\right]_{y=\sqrt{1-(x-2)^2}}^{\sqrt{9-x^2}}\,dx \\ & = \; \tfrac83\pi^2\int_{-3}^1\left\{ -\frac{2-x}{\sqrt{13-4x}} + 1\right\}\,dx + \tfrac83\pi^2\int_1^1 \left\{-\frac{2-x}{\sqrt{13-4x}} + 2-x\right\}\,dx \\ & = \; \tfrac{32}{3}\pi^2 - \tfrac83\pi^2\int_{-3}^3 \frac{2-x}{\sqrt{13-4x}}\,dx \; = \; \tfrac{32}{3}\pi^2 - \tfrac23\pi^2\int_{-3}^3 \left\{\sqrt{13-4x} - \frac{5}{\sqrt{13-4x}}\right\}\,dx \\ & = \; \tfrac{32}{3}\pi^2 - \tfrac23\pi^2\Big[-\tfrac16(13-4x)^{\frac32} + \tfrac52\sqrt{13-4x}\Big]_{-3}^3 \; = \; \tfrac{32}{3}\pi^2 - \tfrac23\pi^2\big(-\tfrac16 + \tfrac52 + \tfrac{125}{6} - \tfrac{25}{2}\big) \; = \; \boxed{\tfrac{32}{9}\pi^2} \end{aligned} so a numerical integration is not necessary.

3 Helpful 0 Interesting 2 Brilliant 0 Confused

@Mark Hennings sir. I am not able to understand the first step of your solution. Please can you explain a bit??

A Former Brilliant Member - 1 year, 8 months ago

Log in to reply

A small volume element d x d y d z dx\,dy\,dz is a distance ( x − 2 ) 2 + y 2 + z 2 \sqrt{(x-2)^2+y^2+z^2} away from the point ( 2 , 0 , 0 ) (2,0,0) , and the line from the volume element to the point ( 2 , 0 , 0 ) (2,0,0) makes an angle θ \theta with the x x -axis, where cos ⁡ θ = x − 2 ( x − 2 ) 2 + y 2 + z 2 \cos\theta \; = \; \frac{x-2}{\sqrt{(x-2)^2+y^2+z^2}} The gravitational force at the point ( 2 , 0 , 0 ) (2,0,0) will (by symmetry) be its component along the x x -axis, which is therefore ∭ G m ρ d x d y d z ( x − 2 ) 2 + y 2 + z 2 cos ⁡ θ \iiint \frac{Gm\rho \,dx\,dy\,dz}{(x-2)^2 + y^2 + z^2} \cos\theta and we are done.

Mark Hennings - 1 year, 8 months ago

Log in to reply

@Mark Hennings sir. Density means mass per unit volume. So why you have multiplied density with mass ?? Can you explain me bit??

A Former Brilliant Member - 1 year, 8 months ago

Log in to reply

@A Former Brilliant Member – The gravitational force between two objects of masses m 1 m_1 and m 2 m_2 is G m 1 m 2 r 2 \frac{Gm_1m_2}{r^2} , where r r is the distance between them. The small volume element has mass ρ d x d y d z \rho\,dx\,dy\,dz , while the test particle has mass m m .

Mark Hennings - 1 year, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...