Forever 2 π ??
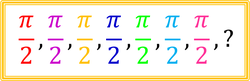 This series will
blow your mind
. Try it!
This series will
blow your mind
. Try it!
What comes next in the following series 2 π , 2 π , 2 π , 2 π , 2 π , 2 π , 2 π can be expressed as q p π . How many digits does the p + q have?
Details and assumptions :
- You may use Wolfram Alpha or other similar programs.
- If you can answer it, you must make the solution!
- You may think this is a bad problem but please do not complain or dispute this problem. This is unrated problem, you have got nothing to lose. If you do not want to answer it, you may ignore it or see the solution instead. Thank you... V(^_^)V
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Looks like only three guys answered this, I thought that Borwein integrals are very famous.
Log in to reply
Hi, @Haroun Meghaichi could you please solve this one and write the solution as a comment. Thanks... :) ∫ 0 1 t 2 0 1 4 ( 1 − t ) 9 9 9 9 d t .
Log in to reply
Using Beta function we get : B ( 2 0 1 5 , 1 0 0 0 0 ) = 1 2 0 1 4 ! 2 0 1 4 ! 9 9 9 9 ! .
Log in to reply
@Haroun Meghaichi – That's correct. You're smart. I'm really sorry if I tested you, I just want to make sure that you answered this question without cheating. Actually, I only regard two people who answer this problem so far, you and Mr. Haussmann. Two thumbs up for you Haroun. d(^_^)b
You're really awesome Mr. Haussmann! Two thumbs up!! d(^_^)b
Consider the following sequence: U 1 U 2 U 3 U 4 U 5 U 6 U 7 AND U 8 = ∫ 0 ∞ x sin x d x = 2 π , = ∫ 0 ∞ x sin x ⋅ ( 3 x ) sin ( 3 x ) d x = 2 π , = ∫ 0 ∞ x sin x ⋅ ( 3 x ) sin ( 3 x ) ⋅ ( 5 x ) sin ( 5 x ) d x = 2 π , = ∫ 0 ∞ x sin x ⋅ ( 3 x ) sin ( 3 x ) ⋅ ( 5 x ) sin ( 5 x ) ⋅ ( 7 x ) sin ( 7 x ) d x = 2 π , = ∫ 0 ∞ n = 1 ∏ 5 ( 2 n − 1 x ) sin ( 2 n − 1 x ) d x = 2 π , = ∫ 0 ∞ n = 1 ∏ 6 ( 2 n − 1 x ) sin ( 2 n − 1 x ) d x = 2 π , = ∫ 0 ∞ n = 1 ∏ 7 ( 2 n − 1 x ) sin ( 2 n − 1 x ) d x = 2 π , = ∫ 0 ∞ n = 1 ∏ 8 ( 2 n − 1 x ) sin ( 2 n − 1 x ) d x = 9 3 5 6 1 5 8 4 9 4 4 0 6 4 0 9 0 7 3 1 0 5 2 1 7 5 0 0 0 0 4 6 7 8 0 7 9 2 4 7 1 3 4 4 0 7 3 8 6 9 6 5 3 7 8 6 4 4 6 9 π . In mathematics, these integrals are called Borwein integrals . This fact is discovered by David and Jonathan Borwein. In general similar integrals have value 2 π whenever the numbers 3 , 5 , 7 ⋯ are replaced by positive real numbers such that the sum of their reciprocals is less than 1 . In the example above, 2 1 + 3 1 + ⋯ + 1 3 1 < 1 , but 2 1 + 3 1 + ⋯ + 1 5 1 > 1 .
Fun fact : After this was discovered by David and Jonathan Borwein, Jonathan verified that the computer algebra software package Maple reports the correct values for all these integrals — and then, as a practical joke, reported this to Maple as a “bug” in the software. Maple computer scientist Jacque Carette reports that “I must have spent three days on this project before I figured out that Jon had tricked me.
# Q . E . D . #
Log in to reply
Please give me a good reason why the answer is not 1, its forming an AP, GP, and everything....
Log in to reply
Isn't the Borwein integrals a good reason?? If you think not, then you can try to answer this series:
What comes next in the following series 2 , 4 , 6 , ?
Log in to reply
@Tunk-Fey Ariawan – I still think a better answer would be 8....
Log in to reply
@Satvik Golechha – There's a lot of better answers for this series. My favorite answer is 9 9 9 , 9 9 9 , 9 9 9 .
Log in to reply
@Tunk-Fey Ariawan – How 999,999,999?
Log in to reply
@Aabhas Mathur – T h e S e r i e s H a s I n f i n i t e S o l u t i o n s , O n e O f T h e P o s s i b l e G e n e r a l T e r m W h i c h C a n G e n e r a t e T h i s S e q u e n c e I s , T n = ( 2 π ) . x [ n / 8 ] , ( x ∈ R − { 0 } ) [ a ] r e p r e s e n t s g r e a t e s t i n t e g e r l e s s t h a n o r e q u a l t o ′ a ′ F r o m T h e G i v e n G e n e r a l T e r m W e G e t T h e S e r i e s 2 π , 2 π , 2 π , 2 π , 2 π , 2 π , 2 π , 2 π . x N o w A s x c a n b e a n y r e a l n u m b e r w e c a n h a v e i n f i n i t e n u m b e r o f s o l u t i o n s
Log in to reply
@Harsh Depal – I would not discuss anything to you until you can explain, who is another Harsh Depal who also answer this problem.
Log in to reply
@Tunk-Fey Ariawan – Population Of India is Around 1.237 billion So it is very much possible that two people have same name and same surname How Do I know who is Other Harsh Depal There might be many other harsh depal you can search on google or facebook
Jeez
Oh my god
Woah! Looks interesting. :D
I think you are asking about the Borwein integrals .