Four Circles in a Box
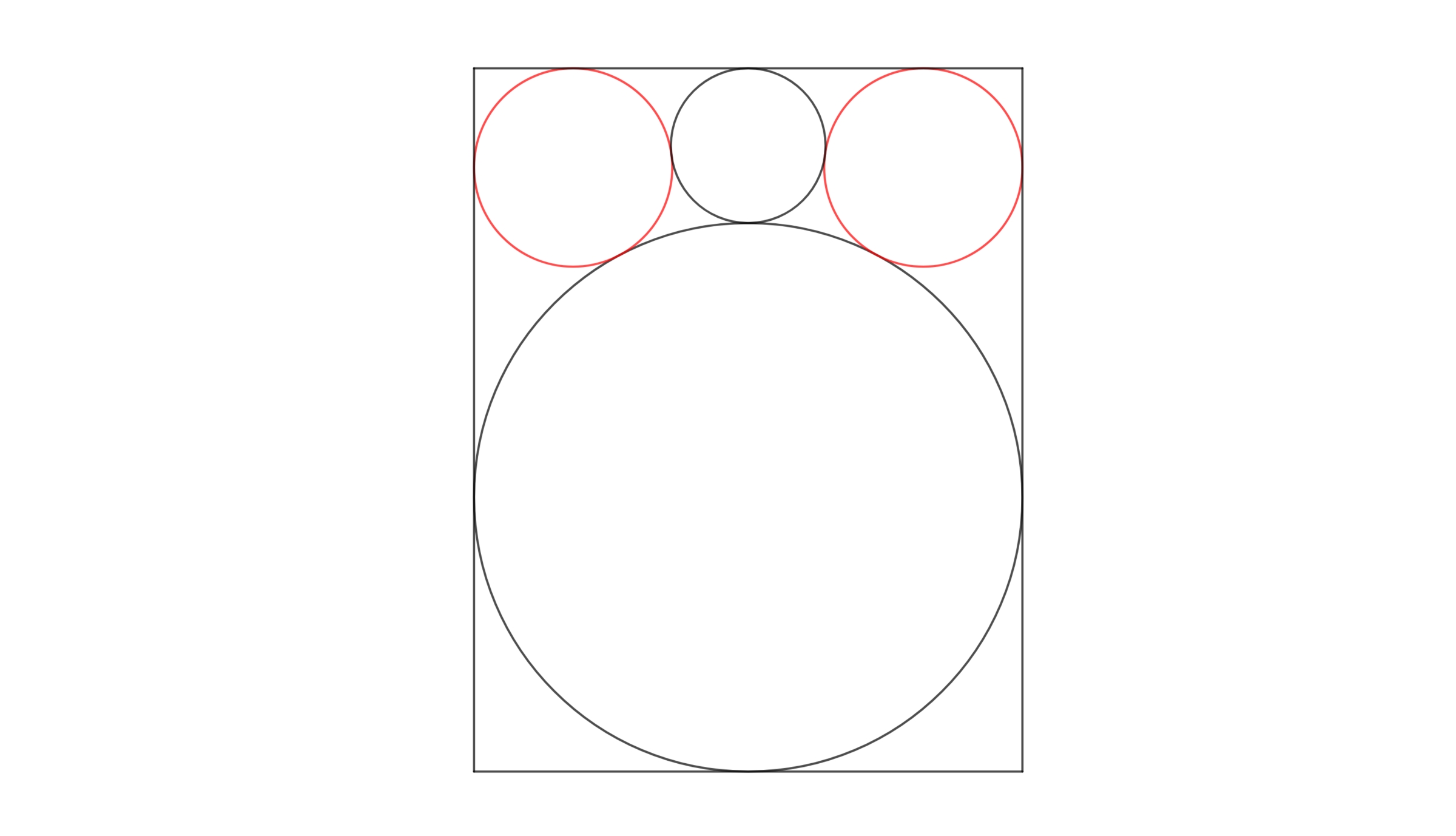
If the red circles are congruent, what is the ratio of the height to the width of the rectangle?
If this ratio is q , submit ⌊ 1 0 5 q ⌋
The answer is 128197.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Log in to reply
Hee, hee. Love Colbert. How do you post images in comments? I've wondered about this for a long time and can't find a way.
Log in to reply
1 |
|
Aesthetically, I much prefer a closed-form solution (as I imagine everyone does), but when the expression involves several radicals, possibly nested, then finding the "correct" form can be as difficult as the problem itself. So this time I requested a decimal solution. Do you have an opinion on which is preferable for problems such as these? closed for with coprime integers or decimal? Or "no big deal, I can solve any problem". :)
In any event, nice work!
Log in to reply
This one beautifully worked out. Nice problem.
Personally, I prefer writing the directive as "Find the closed form of q , then submit your answer as ⌊ 1 0 5 q ⌋ .
Log in to reply
Obviously, there are some questions where specifying a particular form is appropriate; if the "nice" thing about a question is that the result can be written surprisingly concisely, then that's fine, but I don't think that's always (or often) the case.
Here, the "closed form" isn't actually that closed; there are many different ways to write it. Unless it works out very neatly, I personally find it a little frustrating to solve a problem, then spend just as long manipulating surds until I get the required form (especially if that form is completely arbitrary).
On the other hand, it can be annoying as a poster if the range of acceptable numerical answers is too large (I think the tolerance on here is ± 3 % , but I could be wrong).
I think the ⌊ 1 0 k q ⌋ type of form is a very good compromise (and even better with @Pi Han Goh 's wording). I'm curious as to what others think on this, too.
Log in to reply
@Chris Lewis – I wholeheartedly agree with the "good compromise." It makes it harder for users to cheat by drawing close approximations on Desmos and claimed that they got the answer. When in reality, all they did it is toggle and back and forth with some buttons to get a decent approximation.
Equivalently, it's like they only using a Monte Carlo simulation to solve a probability/statistics question, and somehow they feel confident that they got a rigorous result.
Log in to reply
@Pi Han Goh – Yes, I asked for 6 digits to make a desmos solution impractical. I like your suggestion of pointing out that a closed form exists, so folks don't think it's a numerical problem.
Label the top left of the diagram as follows:
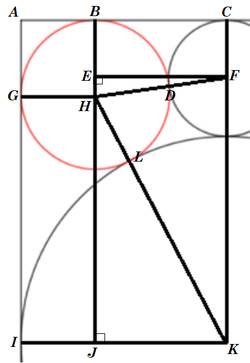
Let the width of the rectangle be 1 , so that the large circle is 2 1 , and let the height of the rectangle be h , so that the ratio is q = 1 h = h , and the radius of the little circle is r = 2 1 ( h − 1 ) . Also, let the radius of a red circle be R .
Since H F = H D + D F = R + r and E H = B H − B E = B H − C F = R − r , by the Pythagorean Theorem on △ E H F we have E F = H F 2 − E H 2 = ( R + r ) 2 − ( R − r ) 2 = 2 R r = 2 2 1 R ( h − 1 ) .
Similarly, since K H = K L + L H = 2 1 + R and J K = I K − I J = I K − G H = 2 1 − R , by the Pythagorean Theorem on △ H J K we have H J = K H 2 − J K 2 = ( 2 1 + R ) 2 − ( 2 1 − R ) 2 = 2 R .
That means A C = A B + B C = G R + E F = R + 2 2 1 R ( h − 1 ) = 2 1 , and A I = A G + G I = B H + H J = R + 2 R = h − 2 1 .
These two equations solve to h = q = 2 1 ( 3 + 2 2 − 5 + 4 2 ) , so ⌊ 1 0 5 q ⌋ = 1 2 8 1 9 7 .
Let the width of the rectangle be 1 . Then the height of the rectangle is q and the radius of the big circle is 2 1 . Let the radius of the two red circles be r 1 and the radius of the small circle be r 2 . Then the (green) line bisecting the rectangle gives
2 r 2 + 1 = q . . . ( 1 )
This length is equal to the vertical component of the green dash line.
r 1 + ( 2 1 + r 1 2 ) 2 − ( 2 1 − r 1 2 ) 2 + 2 1 r 1 + 2 r 1 + 2 1 ( r 1 + 2 1 ) 2 = q = q = q . . . ( 2 )
We can get another equation considering the length of the blue line.
2 r 1 + 2 ( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 2 r 1 + 4 r 1 r 2 = 1 = 1 . . . ( 3 )
With three unknowns and three equations we can solve for q numerically, which I did. But to follow @Pi Han Goh 's tradition ... From ( 3 ) :
r 1 + 2 r 1 r 2 r 1 + 2 r 1 r 2 + r 2 ( r 1 + r 2 ) 2 ( r 1 + r 2 ) 2 ( r 1 + r 2 ) 2 r 1 + r 2 4 r 1 + 4 r 1 r 2 4 r 1 + 1 − 2 r 1 2 ( 2 − 1 ) r 1 + 2 r 1 − 1 2 ( 2 − 1 ) ( q − 2 q + 2 1 ) + 2 q − 2 − 1 ( 2 − 1 ) q + ( 2 − 1 ) q − 1 q + q − 2 − 1 ⟹ q q ⟹ ⌊ 1 0 5 q ⌋ = 2 1 = r 2 + 2 1 = 2 2 r 2 + 1 = 2 q = 2 1 ( r 1 + 2 1 ) 2 = 2 r 1 + 2 1 = 2 2 r 1 + 2 r 1 = 2 2 r 1 + 2 r 1 = 0 = 0 = 0 = 0 = 2 4 2 + 5 − 1 = 2 2 2 + 3 − 4 2 + 5 ≈ 1 . 2 8 1 9 7 1 6 8 = 1 2 8 1 9 7 Note ( 1 ) : 2 r 2 + 1 = q and ( 2 ) : ( r 1 + 2 1 ) 2 = q Multiply both sides by 4 r 1 From ( 3 ) : 2 r 1 + 4 r 1 r 2 = 1 Substitute r 1 = q − 2 1 Multiply both sides by 2 + 1 A quadratic of q