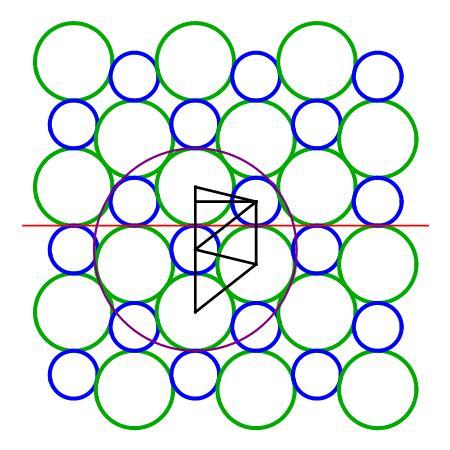
Four Green Two Blue Circles
Four congruent green circles and two congruent blue circles are tangential to one another, to the red chord, and to the large black circle, as shown.
If r 1 is the radius of the green circles and r 2 is the radius of the blue circles, find the ratio r 2 r 1 , which can be expressed as c a + b d , where a , b , c are coprime integers and d is a square-free integer.
Give the answer as the product a × b × c × d .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
That's perceptive of you to pick up the fact that E and E ′ aren't necessarily the same point, even though they turn out to be.
Log in to reply
Thank you! I was trying to find a different way to prove this (with congruent triangles), but I kept running into the problem that I didn't know that E and E' were the same point.
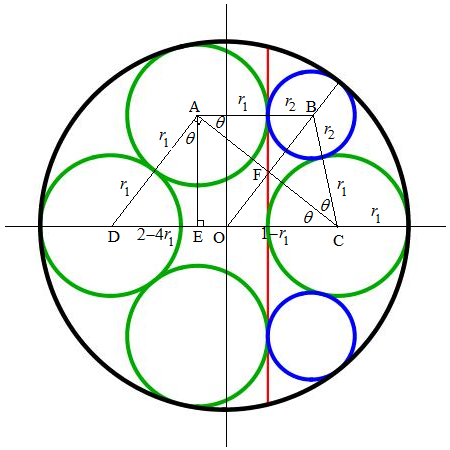
The ratio is the Golden Ratio 2 1 + 5 . See Vreken's excellent solution. Below is how it would look like if the plane was filled with the same green and blue circles, with one red tangent line and purple tangent circle added.
From this we can set up the following equation and solve for r 1 in terms of r 2
( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 + ( 2 r 2 ) 2 = 2 r 1
and thus get us the ratio
r 1 = ( 2 1 + 5 ) r 2
but this seemingly quick solution makes a number of improper assumptions, even if all true. Vreken's solution avoids making those unwarranted assumptions, such as noting that tangent points E , E ′ are not necessarily the same point. The other approach would be to show that it is possible to assemble in this manner green and blue circles in that ratio, and then show that a [purple] circle centered at any blue circle would be tangent to four green and two blue circles, red chord included.
Good that you threw the b factor in there to try and throw us off the scent of the ubiquitous golden ratio. :) Nice problem; hopefully it will be a POTW selection.
Log in to reply
That was the main reason why I decided to post this problem, because once again the golden ratio pops up in a way that doesn't seem obvious why. I'm still looking at other ramifications of this.
Log in to reply
I've just returned to Brilliant after a long time of inactivity and can't seem to find the reshare button. Is it still there?
Log in to reply
@Julian Poon – No, the reshare and "like" options have been deleted. :( You can still save problems, though.
Log in to reply
@Brian Charlesworth – That's a shame, the community's activity a few years ago depended so much on those features.
Log in to reply
@Julian Poon – Yeah, the sense of community on this site isn't what it used to be, unfortunately. :(
Log in to reply
@Brian Charlesworth – I think removing these kinds of feedback is going to dampen the spirit of making contributions to the Community. There's definitely a deadening of "feeling involved".
I hope Brilliant will work to restore that.
@Julian Poon – I noticed that the "Like" button is removed. However, if you want to save the problems you liked, adding to the problem set would be the great idea. :)
It is funny that I guessed the golden ratio correctly by intuition. Even though it is tempting to think there is a hidden equilateral triangle, there are 3 large circles underneath the chord.
I have a lot of confusion from that problem and its answers, but my most important question is how is it possible to tell that the blue cicles and the side green circlues are vertically aligned?
Log in to reply
Because it's mentioned in the question that the circles are kissing each other (those immediately next to them) AND the red line (the closest four). Implying that the 2 'couples' separated by the line are kissing at the same points on it.
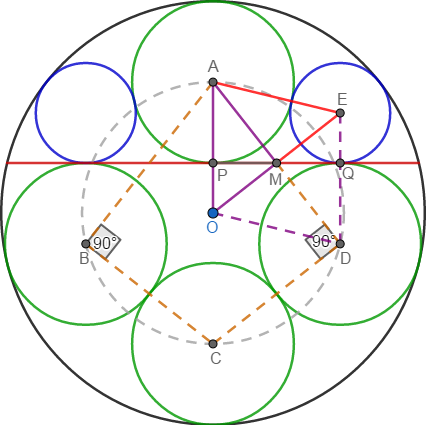
Let the center of the black circle be O and its radius be 1, centers of three green circles be A , C and D and that of a blue circle be B . We note that A , C and D are equidistance from O , therefore △ A C D is inscribed in a circle and C D is a diameter and hence ∠ C A D = 9 0 ∘ . Also note that A B ∣ ∣ C D . Let ∠ A D C = θ ; then ∠ C A B = θ . Since A B = B C = r 1 + r 2 , △ A B C is isosceles and ∠ B C A = θ . △ B C F is a reflection of △ O C F , therefore, C B = C O ⟹ r 1 + r 2 = 1 − r 1 , ⟹ r 2 = 1 − 2 r 1 .
Now sin θ = C D A D = 2 ( 1 − r 1 ) 2 r 1 = 1 − r 1 r 1 . Also sin θ = A D D E = A D C D − C E = 2 r 1 2 − 2 r 1 − 2 r 1 = r 1 1 − 2 r 1 . Note that C E is the sum of 2 r 1 of green circles centered A and C .
Then we have:
1 − r 1 r 1 r 1 2 r 1 2 − 3 r 1 + 1 ⟹ r 1 r 2 = r 1 1 − 2 r 1 = 2 r 1 2 − 3 r 1 + 1 = 0 = 2 3 − 5 = 1 − 2 r 1 = 5 − 2 Note that r 1 < 1
⟹ r 2 r 1 = 2 ( 5 − 2 ) 3 − 5 = 2 ( 3 − 5 ) ( 5 + 2 ) = 2 1 + 5 = φ
Therefore, a × b × c × d = 1 × 1 × 2 × 5 = 1 0 .
Set the origin at the center of the black circle (having radius R), and scale the axes such that the green circles have their centers at distance 1 from the origin. Three of these centers are A=(0,1), B=(0,-1) and C=(x,y). The green circles with centers B and C are touching, so that ( 2 r 1 ) 2 = B C 2 = x 2 + ( y − − 1 ) 2 = x 2 + y 2 + 2 y + 1 = 2 + 2 y (using the fact that 1 = O C 2 = x 2 + y 2 ), so that y + 1 = 2 r 1 2 We also have the horizontal red line touching both green circles so that y + r 1 = 1 − r 1 or y = 1 − 2 r 1 . Substitute this above and we get r 1 2 + r 1 − 1 = 0 which solves as r 1 = 2 5 − 1 Note that r 1 = ϕ − 1 = ϕ 1 . We now also know y = 2 − 5 and R = 1 + r 1 = ϕ . Next, let's set D=(a,b) as the center of the blue circle, (touching the red line and top green circle). We have A D = r 1 + r 2 , O D + r 2 = R and b = 1 − r 1 + r 2 , from which we solve as follows: ( r 1 + r 2 ) 2 = A D 2 = a 2 + ( 1 − b ) 2 = a 2 + b 2 − 2 b + 1 , ( R − r 2 ) 2 = O D 2 = a 2 + b 2 . Subtracting these gives ( r 1 + r 2 ) 2 − ( R − r 2 ) 2 = − 2 b + 1 ,
r 1 2 + 2 r 1 r 2 − R 2 + 2 R r 2 = − 2 b + 1 = − 2 + 2 r 1 − 2 r 2
We already know r 1 and R , filling these values in and working out gives
r 2 = 5 + 1 5 − 1 = 5 + 1 2 r 1
So that r 2 r 1 = ϕ = 2 1 + 5
The requested answer is 1×1×2×5=10.
Note that . . . r 2 , r 1 , 1 , R , . . . are part of a geometric series with factor ϕ .
Finally, by calculating x and a, we can now verify that the circles with centers C and D are not only touching the red line, but also touching each other, something I did not presume. They indeed do: a = x = 4 5 − 8 .
One can show, R=2(r1)+r2 and ratio of (r1/r2) = x, satisfies
x^2-x-1=0, root x =(1/2)(1+√5),
Answer=10
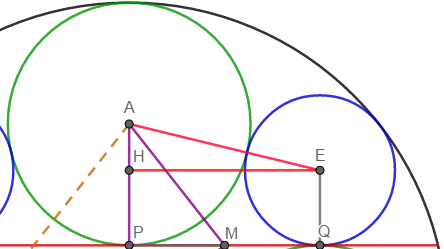
 According to the figure, let:
According to the figure, let:
- A , B , C , and D be the centers of green circles
- E be the center of one of the blue circles
- O be the center of the big circle, and its radius be R
- P be the point where the green circle centered at A touches the chord
- Q be the point where both the blue circle and a green circle touch each other and the chord
- M be the intersection of lines A D and P Q .
Lines A P and D Q are both perpendicular to the chord so A P ∣ ∣ D Q and because A P = D Q = r 1 , A P D Q is a parallelogram. Point M is the intersection of diagonals in A P D Q , so P M = Q M and A M = D M (I assumed that P and Q are not the same points, because of the figure given in the problem).
The distance from O to each of the points A , B , C , and D is R − r 1 , so these four points lie on the same circle. Because of symmetry we have that A C is the diameter of this circle and with that, ∠ A B C = ∠ A D C = 9 0 ° . Line O M connects the midpoints of A C and A D , so O M ∣ ∣ C D and O M = 2 1 C D = 2 1 2 r 1 = r 1 .
From O M ∣ ∣ C D we have ∠ A M O = ∠ A D C = ∠ A P M = 9 0 ° and with ∠ A O M = ∠ M O P , we have △ A M O ∼ △ A P M and so: P M A P = O M A M . Let P M = Q M = x . We know that:
A P P M A M O M P M A P x r 1 x 2 r 1 2 = r 1 = x = A P 2 + P M 2 = r 1 2 + x 2 = r 1 = O M A M = r 1 r 1 2 + x 2 = r 1 2 r 1 2 + x 2
Here, we have a very famous equation which tells us that the ratio of r 1 2 and x 2 might exactly be the golden ratio (or golden number, ϕ = 2 1 + 5 ), but for that to be true we first need to prove that r 1 2 > x 2 . This can be proved if we take a look at one specific triangle:
 Let
H
be a point on
A
P
so that
E
H
⊥
A
P
. We have:
Let
H
be a point on
A
P
so that
E
H
⊥
A
P
. We have:
E H P H A H A E = P Q = P M + M Q = 2 x = E Q = r 2 = A P − P H = r 1 − r 2 = r 1 + r 2
And by triangle inequality:
E H 2 x 2 x r 1 r 1 2 < A H + A E < r 1 − r 2 + r 1 + r 2 < 2 r 1 > x > x 2
And thus: x 2 r 1 2 = ϕ ⇒ x = ϕ r 1
Now, we know that O A = O D = R − r 1 , A E = E D = r 1 + r 2 so △ O A E ≅ △ O D E from which we deduce that O A ∣ ∣ D E and A E ∣ ∣ O D . This gives us: O A = A E = D E = O D i.e. O A E D is a rhombus with M being the intersection of its diagonals as it is the midpoint of A and D and ∠ A M E = 9 0 ° since diagonals in a rhombus are perpendicular to each other. This leads us to ∠ E M Q = 1 8 0 ° − ∠ A M E − ∠ A M P = 9 0 ° − ∠ A M P = ∠ M A P and we have another pair of similar triangles: △ A P M ∼ △ M Q E . Finally:
M P A P x r 1 r 1 r 2 r 1 r 2 r 2 = E Q M Q = r 2 x = x 2 = ϕ r 1 2 = ϕ r 1 r 2 r 1 = ϕ = 2 1 + 5
Сјајно решење! :) Ја сам своје засновао на доказу да је
E
Q
=
O
P
што је очигледно из слике испод. Када се то докаже, лако се одређује
O
P
. (Ознаке дужи које сам овде навео односе се на твоју слику, док су на мојој слици другачије)
Log in to reply
Тачно, покаже се да је O A B C ромб, па из тога следи да је O P = E Q . Мада овде је проблем што не може да се утвди са сигурношћу да ли се плаве и зелене кружнице испод тетиве додирују, иако је то мање-више речено у поставци задатка :'D
Log in to reply
Плаву кружницу сам одредио тако да је увек тангентна зеленим кружницама испод тетиве. Из тога следи да се њен центар подудара са центром велике кружнице. Уколико се узме да је црвена тетива тангента две бочне зелене кружнице, лако се доказује да је нормална на праву која пролази кроз центар велике кружнице и центар доње кружнице. С обзиром да ово својство важи за горњу зелену кружницу из самих услова задатка, следи да се ове праве поклапају тј. да су центри доње зелене, велике и горње зелене кружнице колинеарни. С обзиром да зелене кружнице имају исти радијус следи да су растојања између центра велике кружнице и горње и доње зелене кружнице једнака, респективно. Одатле следи да је заиста плава кружница са центром који се подудара са центром велике кружнице додирује све зелене кружнице.
Направио сам и малу анимацију, али тренутно нажалост не могу да је отпремим.
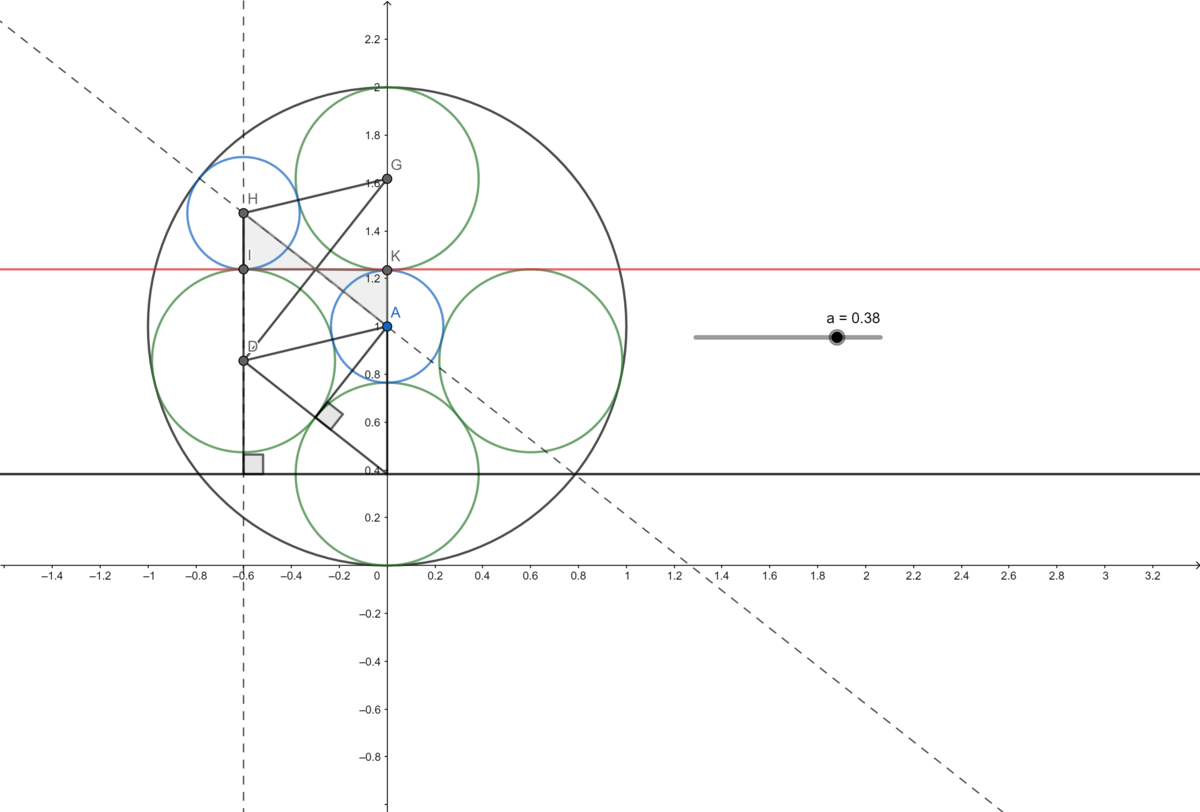
Let A , G , and J be centers of green circles with radii r 1 , C be the center of a blue circle with radius r 2 , and O be the center of the large black circle with radius R . Let B C be an altitude of △ A C O and F G be an altitude of △ G H O , both perpendicular to A H . Finally, let D be the point of tangency of circle A and the red line, E be the point of tangency of circle C and the red line, E ′ be the point of tangency of circle G and the red line, and H be the point of intersection of circle J and A J , as pictured below.
Let O D = t . By symmetry, O H = t . Then O J = O H + H J = t + r 1 , and since O G = R − r 1 and O J = R − r 1 , O G = O J = t + r 1 . Also, D J = O D + O H + H J = 2 t + r 1 , and since D F = E ’ G = r 1 , F J = D J − D F = 2 t + r 1 − r 1 = 2 t and O F = D F − O D = r 1 − t . In addition, G J = 2 r 1 , and let F G = s .
Then using Pythagorean’s Theorem on △ O F G and △ G F J , we have F G 2 + O F 2 = O G 2 and F G 2 + F J 2 = G J 2 , or:
s 2 + ( r 1 − t ) 2 = ( r 1 + t ) 2
s 2 + ( 2 t ) 2 = ( 2 r 1 ) 2
which solves to s = 2 5 − 2 r 1 and t = 2 1 ( 5 − 1 ) r 1 .
Since B O = O D + B D , and B D = C E = r 2 , B O = t + r 2 and A B = A D − B D = r 1 − r 2 . Also, O C = R − r 2 and A C = r 1 + r 2 . Since O J = R − r 1 = t + r 1 , R = t + 2 r 1 , so O C = t + 2 r 1 − r 2 . Let B C = u .
Then using Pythagorean’s Theorem on △ A B C and △ O B C , we have A B 2 + B C 2 = A C 2 and B O 2 + B C 2 = O C 2 , or:
( r 1 − r 2 ) 2 + u 2 = ( r 1 + r 2 ) 2
( t + r 2 ) 2 + u 2 = ( t + 2 r 1 − r 2 ) 2
which with the above t value of t = 2 1 ( 5 − 1 ) r 1 solves to u = 2 5 − 2 r 1 and r 2 = 2 1 ( 5 − 1 ) r 1 (which makes s = u and t = r 2 ).
Therefore, r 2 r 1 = 2 1 ( 5 − 1 ) r 1 r 1 = 2 1 + 5 = ϕ , the golden ratio. This means that a = b = 1 , d = 5 , and c = 2 , and a × b × c × d = 1 0 .