Four Townhouses Logic Puzzle
Aaron, Calvin, David, and Peter each live in one of 4 adjacent townhouses in a row, each of a single color.
 Each owns one pet and imbibes one kind of drink.
Each owns one pet and imbibes one kind of drink.
- Aaron owns the dog.
- The bird lives in the red house.
- Calvin lives in the blue house.
- David does not live in the red house.
- The cat lives where the milk drinker lives.
- Either the fish lives next to the cat or the bird lives next to the coffee drinker.
- If the dog lives in the green house, then the cat lives next to the blue house.
- If Peter owns the fish, then either Calvin owns the bird or else David owns the cat.
- The tea drinker lives two houses away from the coffee drinker.
- The red house resident drinks water if and only if the yellow house resident drinks milk.
Who owns the fish?
Note: Color of residences as shown in photograph have nothing to do with this problem. Also, any pet "owned" is presumed to live in the same place as the owner lives.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Might be reading it incorrectly, but #8 says: If Peter owns the fish, then either Calvin owns the bird or else David owns the cat. Doesn't that mean since Peter doesn't own the fish, neither of the next conditions are true?
Those 5 conditions is all one needs to determine that Calvin has the fish.
Log in to reply
Sir, isn't this the famous "Einstein Riddle"?
Nice problem Sir, really enjoyed it! I confess I got a bit lucky for despite these 5 conditions, I wasn't entirely sure that the answer would be Calvin.
From 8, we get that David owns the cat because Peter doesn't own the fish.
But 8 says "If Peter owns the fish, then either Calvin owns the bird or else David owns the cat."
Since Peter doesn't own the fish, the "or" statement within statement 8 doesn't matter. The whole statement is true because the if statement is false. 8 cannot be used to tell you anything.
Out of the ( 4 ! ) 4 possible permutations of townhouse colors, residents, drinks, and pets, 2 4 of them meet all 1 0 conditions, and in all of them, Calvin lives in a blue house, owns a fish, and drinks either coffee or tea.
Here's one of the solutions
.
| David | Calvin | Peter | Aaron |
| Yellow | Blue | Red | Green |
| Milk | Tea | Water | Coffee |
| Cat | Fish | Bird | Dog |
I'm pretty sure Calvin owns a cat . Okay, for all seriousness, is this problem solvable with just pen and paper?
Log in to reply
Probably not, because while it's not terribly hard to come up with a solution that meets the conditions, proving that Calvin always has the fish in every case takes more work. I suspect that most put down "fish" with the first solution that they come up with. To make sure I don't get egg on my face with this one, I verified this one by computer. So, out of curiosity, do you have a solution that you think meets all ten conditions and Calvin owns the cat? Even if it turns out to be in error, it would interest me a lot, because I've worked hard to get the wording of this problem just right. This puzzle was intended to be an exercise in propositional logic, so this would be good way to go over some of the points.
Logic puzzles like this, to me, is much like solving Pentomino puzzles. Both have a lot in common, and both can have more than one solution. It's a packing problem. Look up "Zebra Puzzle", aka Einstein's Puzzle.
Edit: Oh, you mean "Calvin owns a cat" in jest. I should have clicked that link. Yeah, maybe it's time for me to go off on a hike, it's a nice morning.
Log in to reply
Yup-- Calvin could own a fish or a cat. To prove that it is not necessary that he choose the fish only, can be shown a confirming scenario where this need not happen.
House 1: Yellow (thus water not with red); Aaron; Dog; Water House 2: Red; Peter Bird Tea/Coffee; House 3 b(Calvin)/g (David); cat; milk House 4: b/g c/d; Fish; T/C.
All conditionals satisfied-- disjunct F next to C satisfies 6.
So the problem as set forth is not determinate with respect to C and D.
Log in to reply
@Yale Dikes – @Michael Mendrin can you look into Yale Dikes' comment?
I object to some of the clues. I find 6, 7, and 8 problematical. Six does not clearly indicate that it is an exclusive or. This is necessary to infer the negation of "the bird lives next to the coffee drinker." But worse are the conditionals 7 and 8. When the if clause of a conditional is false as it is for both of these clues, the whole statement is true regardless of the truth or falseness of the conclusion. When the if clause is true, the conclusion must also be true for the whole statement to be true. As such, these two clues contain no usable information, since we can make no inference as to the truth of the conclusions in both cases.
Log in to reply
Your point about 6 is well-taken, in that what would be the "common English usage" in expression an exclusive or , as opposed to the more commonly used inclusive or , which is intended here? How would you suggest re-writing 6 to avoid any misunderstanding that it refers to xor , and not or ?
7 is the simple case of "if-then", that is, "if P is true, then Q is true". The only thing we can infer from that is that if Q is false, then P is false. We can't infer anything else from this.
8 is the combination of the issues both 6 and 7 have, that is, if P is true, then "Q or R is true". The only thing we can infer from this is that if either Q or R is true, then P cannot be false. And by "either Q or R is true", this is to be understood inclusively, i.e., it doesn't matter if both Q and R are true, P still cannot be false.
Nevertheless, this does highlight the difficulty of transitioning from the precise language of prepositional logic to common English, as with word problems involving prepositional logic. If you have suggestions on how to "write the common English" more precisely, I will welcome and consider them.
Edit: As a matter of fact, because of the fact it's been so long since I've checked into this posted problem, I've gone and looked for my original files and I do see that changes in wording have occurred---by whom I have no idea. Maybe you can help me improve the wording?
Log in to reply
"The only thing we can infer from that is that if Q is true, then P cannot be false."
That's completely wrong. Q -> P is the converse of P -> Q, and the converse of a statement is not logically equivalent. ~Q -> ~P is the contrapositive of P -> Q, and a statement IS logically equivalent with its contrapositive. So it would be correct to say "The only thing we can infer from that is that if Q is false, then P cannot be true."
Put another way, the truth table for an if-then statement looks like this:
EDIT: I originally posted the truth table here, but this forum ignores whitespace and made the table look like garbage. Instead, please look up the truth table for a conditional statement.
Given P -> Q, both cases where Q is true are valid, thus meaning you can not determine anything about P if Q is true.
Your assessment of 8 is similarly flawed.
Log in to reply
@Doug Wyltk – I fixed my comment about 7, it's been a long time since I looked at this. What I'd like to know, do you disagree with the answer to the problem, or offer suggestions how to improve the wording in the problem itself? By now, a lot of people have had their fingers on this.
Log in to reply
@Michael Mendrin – I appreciate you taking the time to respond, but I'd honestly rather step away from the problem at this point. I could really wrap myself around it and come up with some suggestions, but it would end up taking a fair amount of time and effort that I'd rather spend elsewhere.
Kudos to you for sticking with it!
Log in to reply
@Doug Wyltk – Well, you know, me too. Meanwhile, welcome to Brilliant? If you'd like see some of my other problems, check out these, Michael Mendrin Problems
Peter Bird Red Tea
Calvin Cat Blue Milk
David Fish Green Coffee
Aaron Dog Yellow Water
- Aaron owns the dog TRUE
- The bird lives in the red house TRUE
- Calvin lives in the blue house TRUE
- David does not live in the red house TRUE
- The cat lives where the milk drinker lives TRUE
- Either the fish lives next to the cat OR the bird lives next to the coffee drinker TRUE - fish is next to cat, bird is not text to coffee drinker
- If the dog lives in the green house, then the cat lives next to the blue house - TRUE. dog is not in green house, cat is not next to blue house
- If peter owns the fish, then either Calvin owns the bird OR else David owns the cat - TRUE: Peter does not own the fish, calvin does not own the bird, david does not own the cat.
- The tea drinker lives two houses away from the coffee drinker - TRUE
- the red house resident drinks water iff the yellow house resident drinks milk - TRUE: yellow does not drink milk and red does not drink water.
This solution meets all 10 conditions, and David owns the fish.
Log in to reply
Close but you don't meet condition #9 since the tea drinker lives only one house away from the coffee drinker. (I.e there is only one house between these two.)
Log in to reply
GL, I think you are confusing two concepts; perhaps it is a language issue. There is a difference between houses between and houses away. That is, if a house is 23 and another is 24 the second house is one space more, or if I added 1 to 2 and got three -- 3 is one number away from two-- though no number is between. If there are two houses between, the number away would be three. The mensus.net puzzles make this distintion crystal clear, as do LSAT games.
The answer is wrong. It should be insufficient information. I give another configuration which meets all the hints:
| Aaron | Calvin | David | Peter |
| Dog | Cat | Fish | Bird |
| Yellow | Blue | Green | Red |
| Water | Tea | Milk | Coffee |
- Aaron owns the dog = TRUE
- The bird lives in the red house = TRUE
- Calvin lives in the blue house = TRUE
- David does not live in the red house = TRUE
- The cat lives where the milk drinker lives = TRUE
- Either the fish lives next to the cat or the bird lives next to the coffee drinker = fish next to cat = TRUE
- If the dog lives in the green house, then the cat lives next to the blue house = dog not in green = TRUE
- If Peter owns the fish, then either Calvin owns the bird or else David owns the cat = peter not own fish = TRUE
- The tea drinker lives two houses away from the coffee drinker = TRUE
- The red house resident drinks water if and only if the yellow house resident drinks milk = red not water AND yellow not milk = TRUE
Andy, I'm probably going to have to kill this problem. It's undergone so many edits by others in efforts to make it "more precisely defined as to provide an unique solution", that I might as well as replace all the wording in English and just replace them with logical expressions. Then maybe everybody can agree on what the unique answer is. I don't blame you if you think "the answer is wrong".
Maybe you can take this up with the Brilliant Staff. This has been going on for years now. Nobody can seem to agree on exactly how the wording should be, "in English". This is an excellent example of why we need mathematical or logical expressions. Now if only we could do the same for law books!
Log in to reply
It's, simple: make the answer David and change statement 8 to "Peter owns the fish if and only if either Calvin owns the bird or David owns the cat". Since the first part of the 'iff' statement is false, the second must be false, meaning David can't own the cat and must rather own the fish.
This configuration does not meet all criteria. The cat does not live with the milk drinker here.
Log in to reply
You're right, it doesn't but I'm still going to post a revised version of this problem.
@Kunal Kantaria You're right. but I still think it does not have enough information to derive the answer logically... (except brute force all possible combinations)
In fact, what I think I'll do is to revise this problem, and repost it. Then I'll redirect traffic from this old one and tell people to not deal with the old version any more. I'll have to find the time to do it, and the real challenge is the exact wording in English. Much harder than the actual logical analysis!
I agree that it is not well determined. I found the following solution where David owns the fish:
| Aaron | David | Calvin | Peter |
| yellow | green | blue | red |
| dog | fish | cat | bird |
| water | coffee | milk | tea |
Aaron owns the dog = TRUE The bird lives in the red house = TRUE Calvin lives in the blue house = TRUE David does not live in the red house = TRUE The cat lives where the milk drinker lives = TRUE Either the fish lives next to the cat or the bird lives next to the coffee drinker = fish next to cat = TRUE If the dog lives in the green house, then the cat lives next to the blue house = dog not in green = TRUE If Peter owns the fish, then either Calvin owns the bird or else David owns the cat = peter not own fish = TRUE The tea drinker lives two houses away from the coffee drinker = TRUE The red house resident drinks water if and only if the yellow house resident drinks milk = red not water AND yellow not milk = TRUE
I have attached an image where I have grouped the data according to the statements.
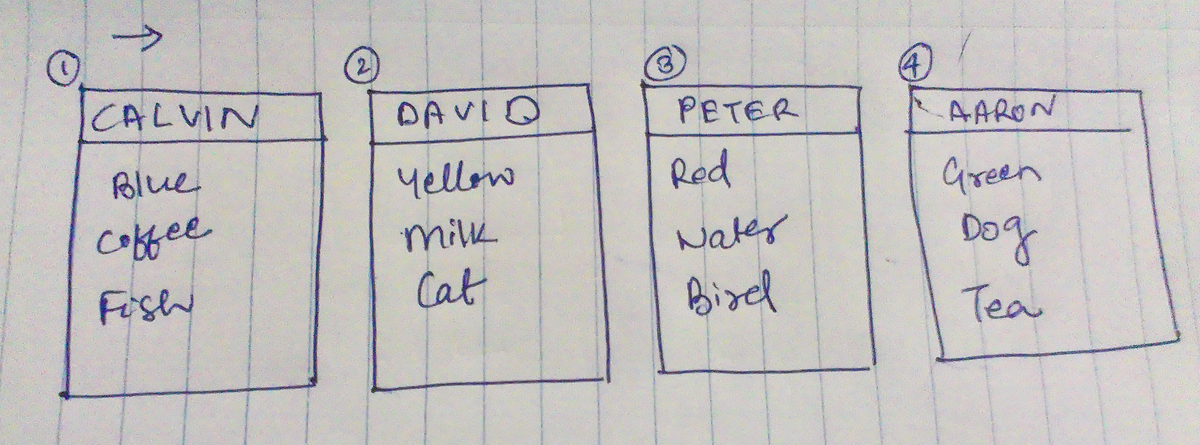
Moderator note:
How did you arrive at that conclusion? What are the sequence of logical steps that you took?
I reach the same conclution.
Log in to reply
Of mohapatra. For me is the only logic way that reach all of the pointa
Got the same answer. Easy one for those who prepared for either CAT or GMAT.
From 1,2,and 3, we know that either David or Peter has both the bird and a red house.
But from 4, we know David does not live in a red house. So Peter must have the bird.
From 8, we get that David owns the cat because Peter doesn't own the fish.
Now we have
Thus, Calvin must own the fish.
P.S. Please correct me if i make any mistakes.