Free Chocolates

Here is how to get the maximum number of chocolates:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

Buying 59049 Chocolates...
Now, I have 59049 chocolates and 59049 wrappers.
Buying 19683 chocolates with 59049 wrappers...
Now, I have 78732 chocolates and 19683 wrappers.
Buying 6561 chocolates with 19683 wrappers...
Now, I have 85293 chocolates and 6561 wrappers.
Buying 2187 chocolates with 6561 wrappers...
Now, I have 87480 chocolates and 2187 wrappers.
Buying 729 chocolates with 2187 wrappers...
Now, I have 88209 chocolates and 729 wrappers.
Buying 243 chocolates with 729 wrappers...
Now, I have 88452 chocolates and 243 wrappers.
Buying 81 chocolates with 243 wrappers...
Now, I have 88533 chocolates and 81 wrappers.
Buying 27 chocolates with 81 wrappers...
Now, I have 88560 chocolates and 27 wrappers.
Buying 9 chocolates with 27 wrappers...
Now, I have 88569 chocolates and 9 wrappers.
Buying 3 chocolates with 9 wrappers...
Now, I have 88572 chocolates and 3 wrappers.
Buying 1 chocolates with 3 wrappers...
Now, I have 88573 chocolates and 1 wrappers.

So, you can get a maximum of $88573$ chocolates.

General solution: For $n, you get $n + \lfloor \frac{n-1}{2} \rfloor$ chocolates.

Vote this solution up if you liked it, thanks.

Every dollar buys 1 chocolate. Each chocolate buys 1/3 of another chocolate. That 1/3 chocolate buys another 1/3 chocolate, and so on. So each dollar buys 1 + 1/3 + 1/9 + 1/27....

We can use the infinite geometric series formula to find that each dollar buys 1/(1-1/3) or 1/(2/3) or 3/2 chocolate bars.

Since he has $59049 dollars he can buy 59049 *1.5 which is 88,573.5. However, you cannot buy half of a chocolate bar so round down to 88,573.

This problem is essentially the infinite geometric series $3^{0}+3^{-1}+3^-{2}...$ and problems like this can be solved like this:

For a series $n^{0}+n^{-1}+n^{-2}+n^{-3}...$ the sum (found limit of series) is $\frac{n}{n-1}$ . If the series is of this form but finite, find the theoretical infinite sum, then floor it (round down)

In this case, it's $\frac{3}{2}$ that you're multiplying by.

chocolate cost = D = $1
you have A = $59,049
you can buy A/D = 59,049 bars
you get x =1 extra bars for recycling y = 3 wrappers
but each bar has z = 1 wrappers
so Az/Dy = 59,049z/3 = +19683
those 19683 will give you an extra 6561
which gives you an exta 2187
which gives you an extra 729
which gives you an extra 243
which gives you an extra 81
which gives you an extra 27
which gives you an extra 9
which gives you an extra 3
which gives you an extra 1

final answer 88573

in this particular case, where you get 1 chocolates for 3 wrappers, we can just use the formula below,

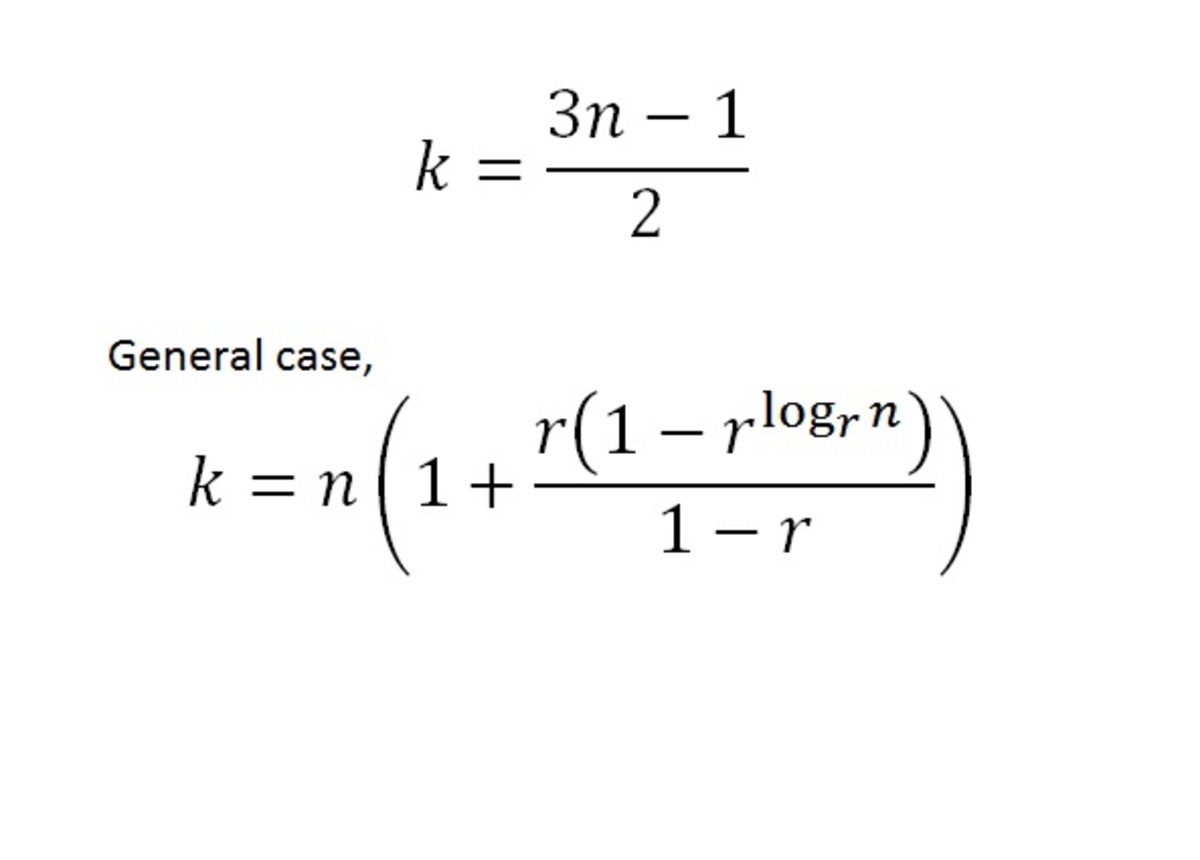
using the first formula, 3*59049 - 1 = 177146, 177146/2 = 88573

where N->amount of money. r->1/no. of wrappers for on chocolate.

and yes you can simplify the formula as u like

Here is the VB.NET code I used:

 Module Module1

Sub Main()
    Dim money As Integer = 59049
    Dim chocolates As Integer = 0
    Dim wrappers As Integer = 0

    While Not money = 0
        money = money - 1
        chocolates += 1
        wrappers += 1
        If wrappers = 3 Then
            chocolates += 1
            wrappers = 1
        End If
    End While
    Console.WriteLine(chocolates)
    Console.ReadLine()
End Sub

 End Module

I did it in QB64 since that's the only language I know so far :( anyways the idea is to create a function, subroutine, or loop that calculates 59049 + 59049/3 +59049/3/3...etc until it reaches 1 (we can assume the answer is an integer).

Python:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

dollars = 59049
wrappers = 0
eaten = 0
while dollars:
    dollars -= 1
    eaten += 1
    wrappers += 1
    if wrappers == 3:
        wrappers -= 3
        eaten += 1
        wrappers += 1
print "Answer:", eaten

You will buy 59049 chocolates with $59049 and then you will have 59049 wrappers. Then with 59049 wrappers, you can buy another 19683 chocolates and with 19683 wrappers you can...

Using the info, you can form a equation and solve -

$x=59049+\frac { 59049 }{ 3 } +\frac { 59049 }{ 9 } \dots \\ \frac { x }{ 3 } =\frac { 59049 }{ 3 } +\frac { 59049 }{ 9 } +\frac { 59049 }{ 27 } \dots\\ x-\frac { x }{ 3 } =59049+\frac { 59049 }{ 3 } -\frac { 59049 }{ 3 } +\frac { 59049 }{ 9 } -\frac { 59049 }{ 9 } +\frac { 59049 }{ 27 } -\frac { 59049 }{ 27 } \dots \\ x-\frac { x }{ 3 } =59049\\ x=88573$

(3n-1)/2 = no of chocolates

it forms an AP like for 3$ - 4 ,5$-7 ,7$-10 so on which is 3$ is first term so add 1 to 3 then for 5$ it s second term so add 2 to 5 so find the position of 59046$ and add it to the amount

What i did was take the amount of money 59049. That would get you 59049 chocolates. Since each one comes wrapped, divide that by 3 to get the number of chocolates you would get from the wrappers, then divide that number by 3 to get another numbrer. keep doing this until you get to one, and then add up all your solutions. 59049+19683+6561+2187+729+243+81+27+9+3+1 for a total of 88573

Essentially, you have two values of candies: the number of chocolates from the initial purchase and the number of chocolates through wrapper trade in. Summing these two values will give you the total number of chocolates. To find the latter value, you must create a summation expression to find the value.

After purchasing the initial amount of chocolate, the number of chocolate you get from the shopkeeper via trade-in becomes: $\frac {59049} {3}$ The wrappers from the trade-in chocolate can also be used to obtain more chocolate. That number is simply: # chocolate received from trade-in / 3 As we continue with this process, we can easily see that this whole process can be expressed as: $\frac {59049} {3^{n}}$ Now that we know this function, the next question we ask ourselves is what is the upper bound. If n is too large, the resulting number from our function becomes a fraction, which we do not want. Thus, in order to find a sufficient n, we simply perform a logarithmic operation to obtain n. The operation is: $log_{3} 59049 = n$ $n = 10$ Now that we have these numbers, we can easily use a summation operation to get the total number of chocolates obtained by the wrapper trade-in policy. Thus: $\sum_{i=1}^10 \frac {59049} {3^{n}}$ Solving the summation will give us 29524. Going back to the first part, we add that number to 59049 to get the total number of chocolates obtained, 88573.

chocolate cost = D = $1 you have A = $59,049 you can buy A/D = 59,049 bars you get x =1 extra bars for recycling y = 3 wrappers but each bar has z = 1 wrappers so Az/Dy = 59,049z/3 = +19683 those 19683 will give you an extra 6561 which gives you an exta 2187 which gives you an extra 729 which gives you an extra 243 which gives you an extra 81 which gives you an extra 27 which gives you an extra 9 which gives you an extra 3 which gives you an extra 1

final answer 88573

THE ans is not 88573 ....... the ans is 78732. ......cuz the general eq.....i have found is ---> n + n%3 (i.e reminder of n/3) + n/3 here take only the integer part of the quotient....and here "n" is $n so, the concept here is for e.g if A is giving 7 dollars.....he gets 7 bars....now he gives 6 wrappers to get 2 bars.....so for now totally he has 9.....now he again give 3 wrapper to get 1 so,,totally he gets 10 chocolates....this follows the same for 59,049.......AND THE FORMULA WORKS CHEERS

As long as you hold one wrapper, you can treat the wrapper recycling as "pay two dollars for three chocolates". This is because you can use the wrapper you have, plus two more wrappers you just got from the two dollars, to obtain another chocolate (and another wrapper). Thus, with $\$59,049$ , we buy one to obtain one wrapper ( $1$ chocolate), then exchange the remaining $\$59,048$ to give $\frac{3}{2} \cdot 59048 = 88572$ chocolates. In total, you obtain $88573$ chocolates, plus one wrapper left.

Note that we need the one wrapper condition. If we only think of "pay two dollars for three chocolates", we will erroneously conclude that $\$2$ gives $3$ chocolates while it only gives $2$ (but if we can borrow one wrapper, it indeed gives $3$ chocolates and we can return the wrapper immediately).

59049+(Sum 59049/3^n from 1 to 59049)

I wrote an equation for this and the only way that I could express it on this comment thread was for me to post it on my website, the answer is 88,573 candy bars. This problem can be solved with a convergent summation of 59,049/(3^n) from n=0 to n=10. There is literally nothing else but the equation on my website. http://seniorsonnet14analysis.com/

I wish there was a way for me to post images in the comments so that I wouldn't have to post it on my website.

Can be simply put as.. For n dollars .. You can buy n choc...then from n wrappers n/3 choc....then n/9 choc from n/3 wrappers and so on....thus total choc u can buy is infinite summation of GP with first term n and common ratio 1/3 ... By logical deduction the exact formula is (3n-1)/2

This is a summation series with formula (1/(3^n)) where n starts from zero to any value you want.