Friction On Stacked Block

A slab (dark brown) of mass m 1 = 4 0 k g rests on a frictionless floor (orange), and a block (light brown) of mass m 2 = 1 0 k g rests on top of the slab. The block m 2 is pulled by a horizontal force F .
What is the greatest force, F max (in N ), such that m 1 and m 2 will move together?
Assumptions and Details
- Use g = 9 . 8 m / s 2
- The coefficients of static friction and kinetic friction between the block and the slab are μ s = 0 . 6 and μ k = 0 . 4 , respectively.
The answer is 73.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why can we not simply say F g e q F f = μ s F N = μ s m 1 g = 5 8 . 8 6 N Where F f is the frictional force between between the block and the slab and F N = F G is the normal force exerted from the slab on the block and the gravitational force respectively?
Log in to reply
Of course in the first line I meant to say F ≤ F f
Log in to reply
The bottom block is accelerating as well, so the impulse on the top block does not go solely into breaking static friction. And the force on the top block has to be greater than the force of static friction for the top block to move.
Another way to think of this is from the perspective of the accelerating top block. The only force it experienced from the accelerating frame of reference is the inertial force of the bottom block pulling back on it. This must be less than the forward force or else the top block wouldn't move.
Log in to reply
@Jacob Swenberg – Thanks for the elaboration. I think I understood it now.
The problem did not explicitly state what value of (/g/) we are to assume, so I assumed a value of 10m/s/s, which resulted in my "incorrect" answer of 75 N instead of 73.5 N if you use 9.8m/s/s. Could you add the value of (/g/) into the problem description? Thanks.
Thank you for your explanation, it really made me understand it. By the way, am I the only one who felt really annoyed that the image is wrong? (block and slab with masses switched)
Log in to reply
Thanks Breno, I am glad that my solution helped. You make a valid point about the inaccuracy in the image. If you find any error / ambiguity in the problem, you can post a report. This will notify the problem creator that there is an error / ambiguity in the problem, and they can rectify it.
You can add a report by clicking on the three dots in the bottom right, and click on "Report problem"
Firstly it is important to note that the question asks about the blocks moving together. This means that blocks will be at rest with respect to each other and hence there will be no relative motion between the blocks. This means that only static friction will act between the blocks.
Lets take a look at the FBD of the two blocks:
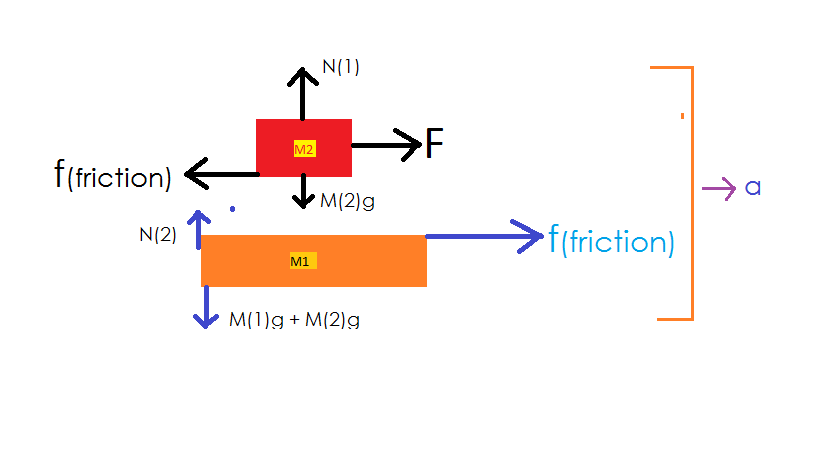
The system of two blocks is moving forward with acceleration a
Along Horizontal, the balance of forces on each mass is given by...
M 2 a M 1 a = F − f = f ( 1 ) ( 2 )
Along vertical:
N 1 = M 2 g ( 3 )
Now substituting value of a from equation (2) in equation (1) , we get F = f ( ( M 1 + M 2 ) / M 1 )
From above equation we clearly see that F= F m a x when f= f m a x
f m a x = μ N 1 g , where μ is coefficient of static friction
Putting
- μ =0.6
- M 2 =10
- M 1 =40
We get f m a x = 58.8
and F m a x = 7 3 . 5
Haha! If the sum of the forces on the upper mass were as you have indicated in your diagram, the upper mass would accelerate upward.
Log in to reply
I find no problem in my solution as well as diagram. Do not make unnecessary comments or post you own solution if you have any problem with mine.
Log in to reply
By the lengths of the arrows indicating the force vectors on the upper block you show a net upward force on that block. I just thought that was funny and did not mean this comment as an insult to you.
You have reversed the role of the two masses from what is given in the accompanying diagram. Therefore, you have the wrong answer. The correct answer is 1176, not taking into account significant figures. To the correct number of significant figures, the answer is 1000.
Log in to reply
And for this I think that I finally entered the correct values according to the question. Just see it carefully and do not make such baseless comments
The only force exerted on the lower block is the friction force from the above block. If the two blocks are to move together, then their accelerations must be equal.
Suppose the frictional force on the lower block is f . The maximum possible value of friction, f max between the two blocks is μ s N . The normal reaction between the blocks is N = m 2 g , therefore f max = μ m 2 g .
Thus, the maximum possible acceleration of the lower block is a max = m 1 f max = m 1 μ m 2 g . This is the limit on the acceleration of the blocks. If both blocks have to move together, then they can't move with acceleration greater than a max .
We can show that the maximum force for which the blocks would move together is F max = ( m 1 + m 2 ) a max :
Suppose the force F were greater than F max , then the acceleration of the center of mass of the blocks would be greater than a max . The acceleration of the lower block cannot be greater than a max , which implies that the acceleration of the upper block is greater than a max . We see that both blocks would have different accelerations, which means that both blocks would move separately.
We have F max = ( m 1 + m 2 ) a max = ( m 1 + m 2 ) m 1 μ m 2 g = ( 4 0 + 1 0 ) × 0 . 6 × 4 0 1 0 × 9 . 8 = 7 3 . 5 N