Friction
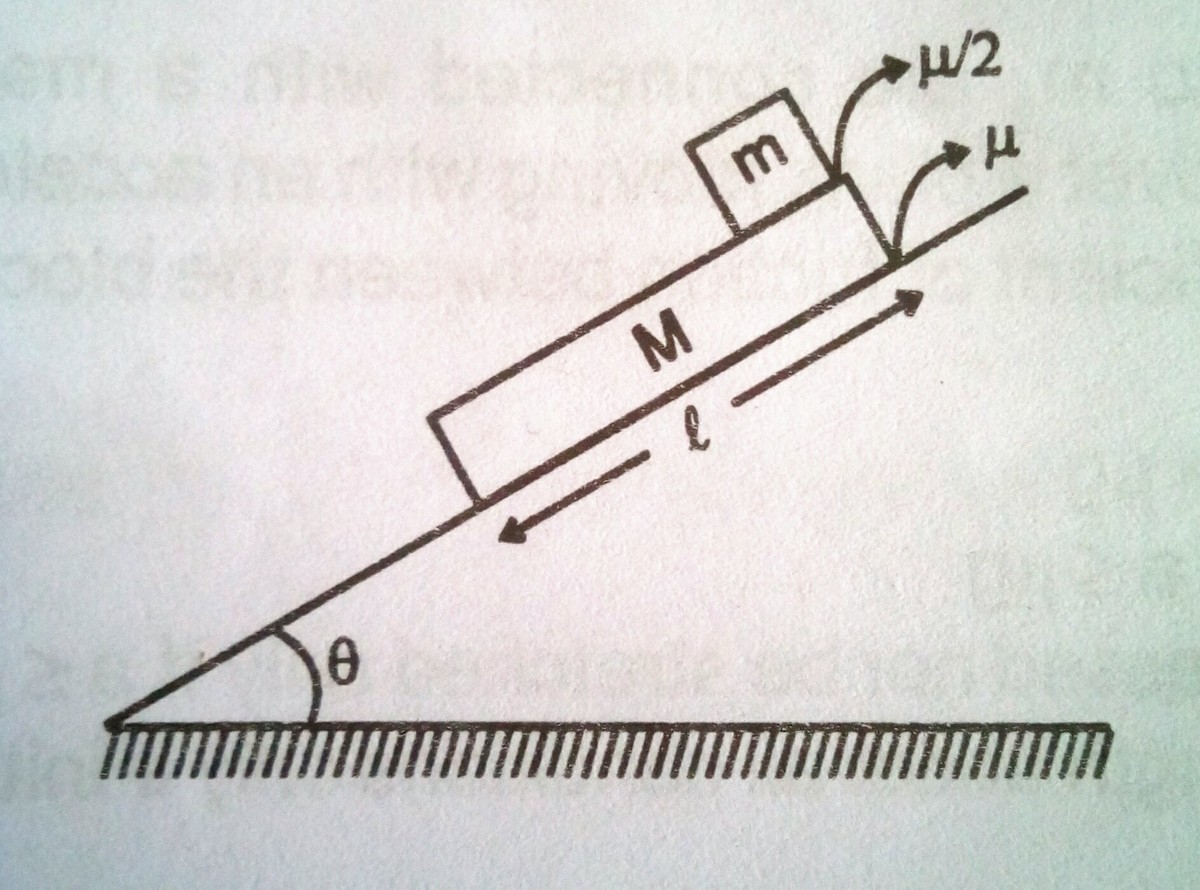
In the above figure it is known that when the blocks are released, they slide. Find the time (in seconds) when the small block will fall off the larger block.
Details and Assumptions
Assume the size of block of mass to be very small.
, , , ,
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that: M=4 Kgr, m=1 Kgr, theta = tan(3/4)= 0.9316, mi=0.4 and l=4 m. Let g=10 m/s^2 , the accelaration a 1 of the larger block is : (M*g*sin(theta) -(M +m)*g*cos(theta)*mi)/M while the accelaration a 2 of the small block is: g sin(theta)-g cos(theta)* 0.5 mi. The small block has to cover a distance l + 0.5 * a_1 *t^2 in t seconds, so we get: l + 0.5 * a_1 *t^2 = 0.5 a 2 *t^2 or t = sqrt(2*l/(a 2 - a_1). We find that t is 2.1143 seconds or about 2 seconds.