Friction Exercise
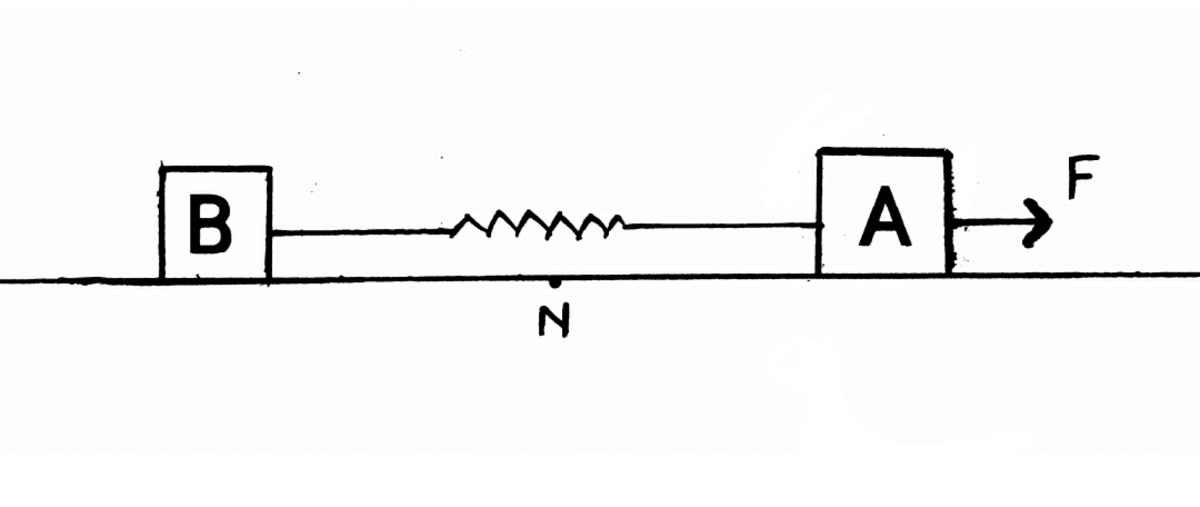
Two blocks are connected with each other with the help of spring and threads.
Consider
N
as origin of the system.
Find the
F
m
i
n
required to move the block
B
.
Details and Assumptions
1)
M
A
=
2
0
2)
M
B
=
1
0
3)
For
x
<
0
,take
μ
=
0
.
2
5
4)
For
x
≥
0
,take
μ
=
0
.
7
5
5)
The springs and threads used in the system are massless.
6)
Gravity is acting downwards.
7)
g
=
1
0
8)
Neglect air resistance
9)
Neglect the gravitational force between the blocks.
10)
Consider everything in SI units.
11)
The distance between the origin and block
B
is very large.
The problem is modification of a non-original problem.
I would be happy if anyone will upgrade this problem.
The answer is 162.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nicely done. In your first line, it should be 150 instead of 100
Log in to reply
@Steven Chase
sir can you upgrade this problem?
Like we can add
1)
varying
μ
with distance.
2)
varying mass in block
3)
Air resistance.
Log in to reply
Are you asking me to? If so, I can probably do that
Log in to reply
@Steven Chase
–
@Steven Chase
yes sir.
If I will make that changes, it is obvious you will report it.
I have a doubt about the equation of motion above F m i n = 2 1 k x + 1 5 0 ; I'm getting the wrong result. Since the force of the spring on both the right and left side is k x , drawing a free-body diagram, we get that the minimum force is equal to the friction for block A and the force of spring acting opposite to the motion of block a, which should be k x . I think I'm missing something lol.
Anyway, the equation I'm getting is 1 5 0 + k x = F m i n
Hope you can help me here; thanks mate!
@Krishna Karthik
Bro don't make free body diagram.
Just write work energy equation.
And can you show your whole free body diagram??
Log in to reply
Oh, no problem, I realised the error. Good problem man! :)
Log in to reply
Thanks bro.
Can you make a note on Simpson
3
1
rule and
8
1
rule for evaluating integrals.
Thanks in advance.
The friction forces for block A and block B are 1 5 0 and 2 5 , respectively. My approach consists of a "virtual laboratory". The process is:
1) Try different values of F , starting with something slightly greater than 1 5 0 .
2) For each F , run the time domain simulation until block A stops (starts to move backward after initially moving forward). This is the point at which the spring force is greatest
3) Compare the final spring force against the friction force for block B . The minimum required value of F is the value of F for which the final spring force is equal to the friction force for block B . This minimum value comes out to be 1 6 2 . 5 .
Code is attached.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
|
@Steven Chase
sir thanks for code.
BTW solving analytically is pure fun.
@Steven Chase sir i have uploaded my solution.
@Steven Chase sir you new problem Wedge block and spring can be solved through anaylitical way????
Log in to reply
I think the best way to tackle it is with a combination of analytical work and numerical simulation
Log in to reply
@Steven Chase without Lagrange is it possible to solve that problem?
Log in to reply
@A Former Brilliant Member – I doubt it
Log in to reply
@Steven Chase – @Steven Chase how much time will it take me to learn lagrange??
Log in to reply
@A Former Brilliant Member – Perhaps a few hours
Log in to reply
@Steven Chase
–
@Steven Chase
Literally , I want to learn NOW.
Can young share a pdf, I will learn that thoroughly.
Log in to reply
@A Former Brilliant Member – Here is a good place to start. I will also put up a solution to that problem.
https://brilliant.org/wiki/lagrangian-formulation-of-mechanics/
In my solution, I will not explain all the steps.
F m i n x = 2 1 k x 2 + 1 5 0 x
As we know ,to move k x = 2 5
1 5 0 + 2 1 k x = F m i n
F m i n = 1 6 2 . 5