0 Solver Challenge (Level 6 Mechanics)
In the diagram below, the coefficient of friction between the block and the circular loop is μ . What should be the minimum velocity given to the block so that it just reaches the topmost point of the loop?
If the velocity is of the form v o = a g R ( e b π μ m − p μ q + 1 c ( d μ n − 1 ) ( e f π μ j + 1 ) ) , where a , b , c , d , f , p , m , n , j , q are all positive integers, find a + b + c + d + f + p + m + n + j + q .
Hint: Use linear differential equation.
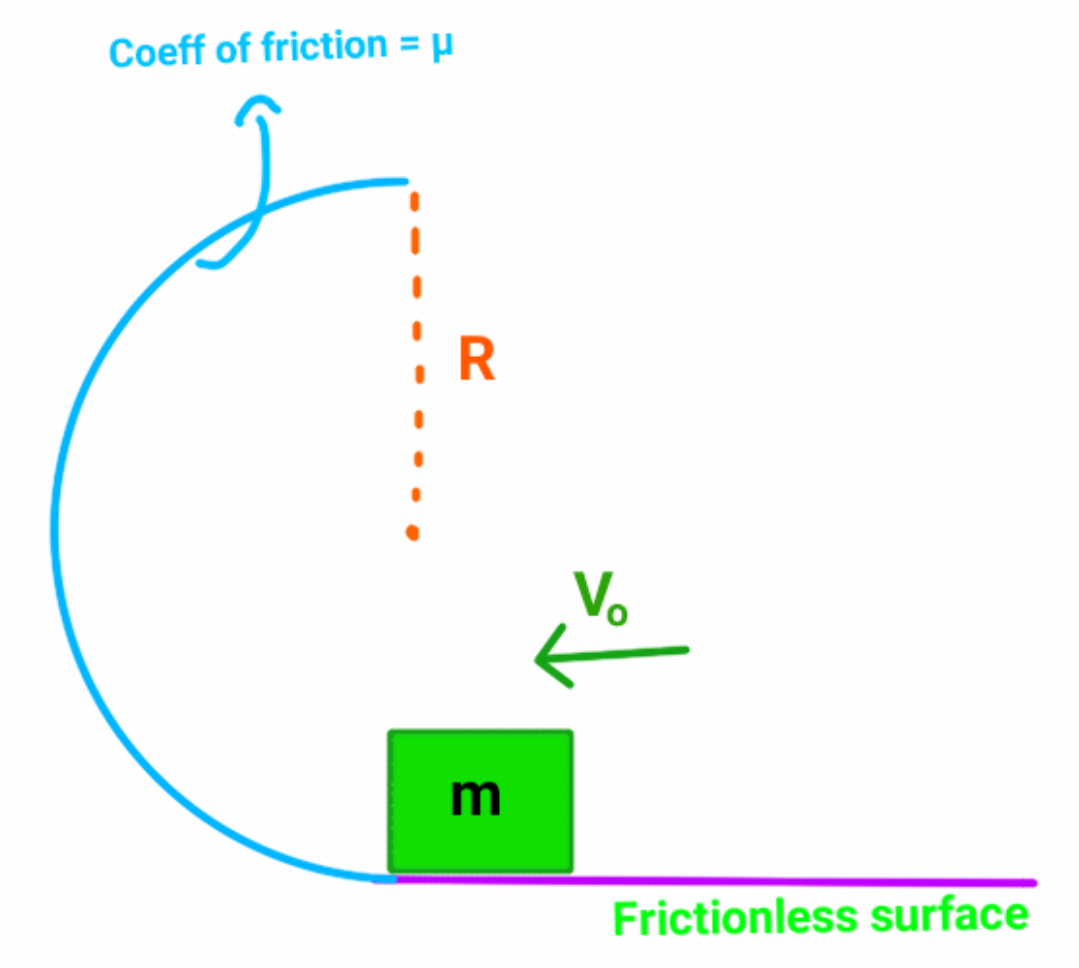
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
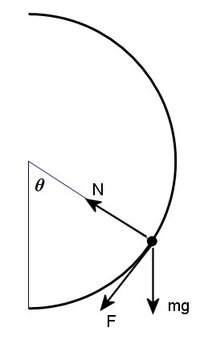 If
θ
is the angle the radial line to the particle makes with the vertical, the tangential equation of motion is
m
R
θ
¨
=
−
F
−
m
g
sin
θ
=
−
μ
N
−
m
g
sin
θ
while the radial equation of motion is
m
R
θ
˙
2
=
N
−
m
g
cos
θ
Putting these equations together, we see that
m
R
θ
¨
+
m
g
sin
θ
+
μ
(
m
R
θ
˙
2
+
m
g
cos
θ
)
R
(
θ
¨
+
μ
θ
˙
2
)
+
g
(
sin
θ
+
μ
cos
θ
)
d
θ
d
[
2
1
R
θ
˙
2
e
2
μ
θ
]
+
g
(
sin
θ
+
μ
cos
θ
)
e
2
μ
θ
2
1
R
θ
˙
2
e
2
μ
θ
+
4
μ
2
+
1
g
[
(
2
μ
2
−
1
)
cos
θ
+
3
μ
sin
θ
]
e
2
μ
θ
=
0
=
0
=
0
=
2
R
v
0
2
+
4
μ
2
+
1
g
(
2
μ
2
−
1
)
and hence
R
θ
˙
2
m
1
N
=
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
θ
−
4
μ
2
+
1
2
g
[
(
2
μ
2
−
1
)
cos
θ
+
3
μ
sin
θ
]
=
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
θ
+
4
μ
2
+
1
3
g
[
cos
θ
−
2
μ
sin
θ
]
The least velocity that will enable the particle to reach the top is the one for which
N
=
0
for the first time at
θ
=
π
. For
N
to be
0
when
θ
=
π
we require that
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
π
R
v
0
2
v
0
=
4
μ
2
+
1
3
g
=
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
=
R
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
Notice that, for this value of
v
0
, we have
N
d
θ
d
N
=
4
μ
2
+
1
3
m
g
[
e
2
μ
(
π
−
θ
)
+
cos
θ
−
2
μ
sin
θ
]
=
−
4
μ
2
+
1
3
m
g
[
2
μ
(
e
2
μ
(
π
−
θ
)
+
cos
θ
)
+
sin
θ
]
and hence it is clear that
d
θ
d
N
≤
0
for all
0
<
θ
<
π
, so we deduce that
N
≥
0
for all
0
≤
θ
≤
π
.
Thus the smallest value of
v
0
for which the particle gets to the top is
v
0
=
R
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
which makes the answer
1
+
2
+
2
+
2
+
2
+
4
+
1
+
2
+
1
+
2
=
1
9
.
If
θ
is the angle the radial line to the particle makes with the vertical, the tangential equation of motion is
m
R
θ
¨
=
−
F
−
m
g
sin
θ
=
−
μ
N
−
m
g
sin
θ
while the radial equation of motion is
m
R
θ
˙
2
=
N
−
m
g
cos
θ
Putting these equations together, we see that
m
R
θ
¨
+
m
g
sin
θ
+
μ
(
m
R
θ
˙
2
+
m
g
cos
θ
)
R
(
θ
¨
+
μ
θ
˙
2
)
+
g
(
sin
θ
+
μ
cos
θ
)
d
θ
d
[
2
1
R
θ
˙
2
e
2
μ
θ
]
+
g
(
sin
θ
+
μ
cos
θ
)
e
2
μ
θ
2
1
R
θ
˙
2
e
2
μ
θ
+
4
μ
2
+
1
g
[
(
2
μ
2
−
1
)
cos
θ
+
3
μ
sin
θ
]
e
2
μ
θ
=
0
=
0
=
0
=
2
R
v
0
2
+
4
μ
2
+
1
g
(
2
μ
2
−
1
)
and hence
R
θ
˙
2
m
1
N
=
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
θ
−
4
μ
2
+
1
2
g
[
(
2
μ
2
−
1
)
cos
θ
+
3
μ
sin
θ
]
=
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
θ
+
4
μ
2
+
1
3
g
[
cos
θ
−
2
μ
sin
θ
]
The least velocity that will enable the particle to reach the top is the one for which
N
=
0
for the first time at
θ
=
π
. For
N
to be
0
when
θ
=
π
we require that
(
R
v
0
2
+
4
μ
2
+
1
2
g
(
2
μ
2
−
1
)
)
e
−
2
μ
π
R
v
0
2
v
0
=
4
μ
2
+
1
3
g
=
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
=
R
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
Notice that, for this value of
v
0
, we have
N
d
θ
d
N
=
4
μ
2
+
1
3
m
g
[
e
2
μ
(
π
−
θ
)
+
cos
θ
−
2
μ
sin
θ
]
=
−
4
μ
2
+
1
3
m
g
[
2
μ
(
e
2
μ
(
π
−
θ
)
+
cos
θ
)
+
sin
θ
]
and hence it is clear that
d
θ
d
N
≤
0
for all
0
<
θ
<
π
, so we deduce that
N
≥
0
for all
0
≤
θ
≤
π
.
Thus the smallest value of
v
0
for which the particle gets to the top is
v
0
=
R
g
(
e
2
μ
π
−
4
μ
2
+
1
2
(
2
μ
2
−
1
)
(
e
2
μ
π
+
1
)
)
which makes the answer
1
+
2
+
2
+
2
+
2
+
4
+
1
+
2
+
1
+
2
=
1
9
.
Accurate sir!
Log in to reply
The question says "e" is also a positive integer & has been asked in the final sum also. I think it should be mentioned that its the euler's number & should not be included in the sum which gives the correct answer.
Log in to reply
Hmm.. correct. This question have many small loopholes .. sorry
Log in to reply
@Md Zuhair – I am afraid you have not fixed matters. The number e should be Euler's number, and not a variable, so we do not need α .
I have edited the problem, restoring e and removing α (we only want ten integer variables - see my solution). In the interests of clarity, I have replaced i by p , so that nobody confuses it with the square root of − 1 .
Log in to reply
@Mark Hennings – Ok.. Ya sir, you are absolutely correct. :) Thanks sir. Btw, do sir are you in stack ?
Log in to reply
@Md Zuhair – I guess he is in UK.
Log in to reply
@Harsh Shrivastava – Ha.. he is in UK. So? Is it so that UK people cannot use stack?
great question!!!!! Is this original ?
Log in to reply
I thought about it... :P.. but there is a problem
Log in to reply
thats great!!!! you are in 11th and you know linear diiferential equation.....thats awesome!!!!!
Log in to reply
@A Former Brilliant Member – Initially I thought I solved it wrong and gave it....... d when saw Mark Hennings sir did it.... I was sure abt the answer. Tha ks btw. I knew LDE frm 10th.. well applying in phy is tough
Log in to reply
@Md Zuhair – your are smart!!!! i came to know about LDE only in 12th when we were formally taught differential equations.
Log in to reply
@A Former Brilliant Member – That doesnt matter. JEE doesnt sees the knowledge.. it checks the depth in knowledge+IQ which you have :)
Log in to reply
@Md Zuhair – well it all depends on what happens on "that day"
fantastic question!!! AND An really awesome solution by Mark Hennings!!
@Md Zuhair please post more question like this.
Can someone please explain how did the 8th and 9th lines ( start with d/d(Theta) ) come ?
Log in to reply
Note that θ ¨ = d θ d ( 2 1 θ ˙ 2 ) . Then e 2 μ θ is the integrating factor for the DE, which gives line 8. Line 9 comes from integrating line 8 with respect to θ , and applying the initial conditions to determine the constant of integration.
Log in to reply
Thank you very much Mr. Mark , actually , my real confusion is how did come θ ¨ = d θ d ( 2 1 θ ˙ 2 ) ? , is there any link or keyword for the proof or explanation to that ?
Log in to reply
@Ahmed Aljayashi – The Chain Rule tells us that θ ˙ × d θ d ( 2 1 θ ˙ 2 ) = d t d ( 2 1 θ ˙ 2 ) = θ ˙ × θ ¨ and the result follows.
Incidentally, this trick is really useful throughout Mechanics. For example, consider a particle moving in a vertical straight line under the influence of gravity and an external force F . Then m x ¨ = − m g + F and hence d x d ( 2 1 m x ˙ 2 + m g x ) = F so that 2 1 m x ˙ 2 + m g x = ∫ F d x + c which is the work-energy relation.
Log in to reply
@Mark Hennings – I'm very grateful to you , this was clear and helpful .
@Mark Hennings how you come from 4th to 5th line. please. ???
Log in to reply
@A Former Brilliant Member – I think I have already answered this. Isn't what you ask the same as Ahmed' question?