A rough slide

Classical Mechanics Level 4

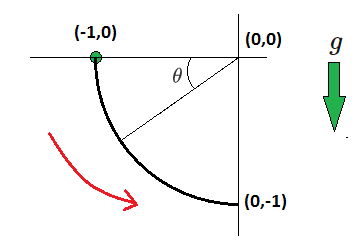
A $\SI{1}{\kilo\gram}$ bead slides from rest under the pull of gravity from the point $\left(\SI{-1}{\meter}, \SI{0}{\meter}\right)$ to the point $\left(\SI{0}{\meter}, \SI{-1}{\meter}\right)$ along a wire in the shape of a circle centered on the origin, as shown above.

The wire is rough, and exerts a retarding tangential friction force $F_f = \mu F_\textrm{normal}$ on the bead, with $\mu = \frac{1}{2}.$

Find the speed of the bead $($ in $\text{m/s})$ when it arrives at $\left(\SI{0}{\meter},\SI{-1}{\meter}\right).$

Note: $g = \SI[per-mode=symbol]{10}{\meter\per\second\squared}.$

The answer is 1.37.

2 solutions

Mark Hennings
Apr 18, 2017

Let $\theta$ be the angle that the radius to the particle makes with the downward vertical, $r$ the radius and $m$ the mass of the particle. If $N$ is the normal reaction, and $F = \mu N$ the friction force on the particle, then the radial and transverse equations of motion are: $N - mg\cos\theta \; = \; mr\dot\theta^2 \hspace{2cm} \mu N - mg\sin\theta \; = \; mr\ddot{\theta}$ Eliminating $N$ yields $\begin{aligned} mr\ddot\theta - \mu mr \dot\theta^2 & = mg(\mu\cos\theta - \sin\theta) \\ \ddot\theta - \mu \dot\theta^2 & = \frac{g}{r}\big(\mu\cos\theta - \sin\theta) \\ \frac{d}{d\theta}\big[\tfrac12\dot\theta^2 e^{-2\mu\theta}\big] & = \frac{g}{r}(\mu\cos\theta - \sin\theta)e^{-2\mu\theta} \end{aligned}$ Since the particle starts at rest when $\theta = \tfrac12\pi$ , the particle's speed at angle $\theta$ is $v(\theta)^2 \; = \; 2rge^{2\mu\theta}\int_{\theta}^{\frac12\pi}(\sin\theta - \mu\cos\theta)e^{-2\mu\theta}\,d\theta$ With $r=1$ , $g=10$ , $\mu=\tfrac12$ , the particle's speed at the bottom is $v(0)$ , where $v(0)^2 \; = \; 10\int_0^{\frac12\pi}(2\sin\theta - \cos\theta)e^{-\theta}\,d\theta \; = \; 5\big(1 - 3e^{-\frac12\pi}\big)$ and hence the answer is $v(0) = \boxed{1.37179}$ .

I'm impressed. How complex do you think the path can get before purely analytical solutions become impossible? Or perhaps infeasible, if not strictly impossible.

Steven Chase - 4 years, 1 month ago

If you look at my further note, I set out a fairly general case. Obtaining the first integral of the equations explicitly - basically, the energy equation - requires us to perform an integral that could be seriously difficult, if not impossible.

Mark Hennings - 4 years, 1 month ago

I just have a question, if the path would have been say a Sine wave instead of a circle how would we have dealt with that ?

Aditya Narayan Sharma - 4 years, 1 month ago

Friction $\mathbf{F}$ would act tangentially to the curve, and the normal reaction $\mathbf{N}$ would act along the principal normal. If the curve was the shape $y = f(x)$ , then the position vector of the particle would be $\mathbf{r} \; = \; (x,f(x))$ and we can differentiate this twice to obtain the equation $m\ddot{\mathbf{r}} \; = \; \mathbf{N} + \mathbf{F} + mg(0,-1)$ The only unknown on the RHS is the modulus of $\mathbf{N}$ (all the vector directions can be expressed in terms of $f(x)$ ). We could take components and thereby eliminate this, obtaining a differential equation for $x$ .

Mark Hennings - 4 years, 1 month ago

Actually I am a bit confused about the last equation. How differentiating twice we obtain that. It would be very helpful for me if you please explain it a bit if you have time.

Aditya Narayan Sharma - 4 years, 1 month ago

@Aditya Narayan Sharma – Suppose that the wire has shape given by the equation $y = f(x)$ , where $f$ has a minimum at $x=0$ . The position vector of the particle is $\begin{aligned} \mathbf{r} & = {x \choose f(x)} \\ \dot{\mathbf{r}} & = {1 \choose f'(x)} \dot{x} \\ \ddot{\mathbf{r}} & = {1 \choose f'(x)} \ddot{x} + {0 \choose f''(x)} \dot{x}^2 \end{aligned}$ and we must have $\mathbf{N} \; = \; \lambda {-f'(x) \choose 1} \hspace{2cm} \mathbf{F} \; = \; \mu\lambda {1 \choose f'(x)}$ for some function $\lambda$ . Recall that $\mathbf{F}$ has to be tangential to the curve, while $\mathbf{N}$ has to be normal to the curve and upward-pointing. The equation of motion is $\begin{aligned} m\ddot{\mathbf{r}} & = \mathbf{N} + \mathbf{F} + mg{0 \choose -1} \\ m{1 \choose f'(x)} \ddot{x} + m{0 \choose f''(x)} \dot{x}^2 & = \lambda {-f'(x) \choose 1} + \mu\lambda {1 \choose f'(x)} + mg{0 \choose -1} \end{aligned}$ Taking the scalar product of this equation with ${1 \choose f'(x)}$ and ${-f'(x) \choose 1}$ , we obtain $\begin{aligned} m\big(1 + f'(x)^2\big)^2 \ddot{x} + mf'(x)f''(x)\dot{x}^2 & = \mu\lambda\big(1 + f'(x)^2\big) - mgf'(x) \\ mf''(x)\dot{x}^2 & = \lambda\big(1 + f'(x)^2\big) - mg \end{aligned}$ Eliminating $\lambda$ yields $\begin{aligned} \big(1 + f'(x)^2\big)\ddot{x} + \big(f'(x)f''(x) - \mu f''(x)\big)\dot{x}^2 & = g\big(\mu - f'(x)\big) \\ \frac{d}{dx}\Big[\tfrac12\big(1 + f'(x)^2\big)e^{-2\mu\tan^{-1}f'(x)} \dot{x}^2\Big] & = g\big(\mu - f'(x)\big)e^{-2\mu \tan^{-1}f'(x)} \end{aligned}$ At this point, we would need to know the explicit form of $f(x)$ to proceed further...

Mark Hennings - 4 years, 1 month ago

@Mark Hennings – Thanks a lot, This was an awesome explanation.

Aditya Narayan Sharma - 4 years, 1 month ago

@Aditya Narayan Sharma – How do you move from step 3 to step 4? How does $e^{-2\mu\theta}$ appear in the step 4?

Rohit Gupta - 4 years, 1 month ago

@Rohit Gupta – It is a matter of looking for an integrating factor. Since $\frac{d}{d\theta} \big(\tfrac12\dot\theta^2\big) = \ddot\theta$ , multiplying by $e^{-2\mu\theta}$ is what it takes to make the LHS of the equation exact.

Mark Hennings - 4 years, 1 month ago

@Mark Hennings – Well, this is a very clever adjustment. Is there a method to follow to find such integrating factors or one has to do the hit and trail approach to reach to it?

Moreover, in the second equation, $\mu N - mg\sin\theta \; = \; mr\ddot{\theta}$ , should it be $mg\sin\theta - \mu N \; = \; mr\ddot{\theta}$ ? This is because the speed is increasing, thus the forces in the direction of the speed must be greater.

Rohit Gupta - 4 years, 1 month ago

@Rohit Gupta – Look up solving first order differential equations for the technique for finding integrating factors. In brief, the integrating factor for the equation $\frac{dy}{dx} + a(x)y \; = \; b(x)$ is $e^{\int a(x)\,dx}$

My equation is correct, Firstly, my $\theta$ is not the $\theta$ that Steven used. It is the angle with the downward vertical. Thus, while $\theta$ is positive, $\dot\theta$ and $\ddot\theta$ are negative. The tangential component of gravity acts in the direction of negative $\theta$ , and the friction force acts in the opposite direction.

Mark Hennings - 4 years, 1 month ago

@Mark Hennings – the theta' term disappeared because the derivative is wrt theta right? clever!

Dhruv G - 4 years, 1 month ago

@Dhruv G – If you prefer, multiply the whole equation by $\dot\theta$ and then integrate with respect to $t$ .

Mark Hennings - 4 years, 1 month ago

Steven Chase
Apr 18, 2017

See @Mark Hennings for a purely analytical approach. I will provide a hybrid analytical-computational solution which eases the mathematical burden, with a computer taking up the slack.

Split the gravitational force into two parts. The tangential component is:

$\large{F_{gt} = mg \, cos\theta}$

The normal component is (referenced toward the origin):

$\large{F_{gn} = -mg \, sin\theta}$

Write an expression for the centripetal force in relation to the normal reaction force and the normal component of the gravity force. Let the variable $v$ refer to the bead's speed.

$\large{F_{c} = \frac{mv^2}{R} = -mg \, sin\theta + F_{nr} \implies F_{nr} = mg \, sin\theta + \frac{mv^2}{R} }$

The net tangential force with friction is therefore:

$\large{F_{t} = mg \, cos\theta - \mu \Big[mg \, sin\theta + \frac{mv^2}{R}\Big] = m \frac{dv}{dt} \\ \frac{dv}{dt} = \dot{v} = g \, cos\theta - \mu \Big[g \, sin\theta + \frac{v^2}{R}\Big] }$

Then we can solve iteratively in the following way (I used a time step $\Delta t = 10^{-6} sec$ ):

$\large{v_k = v_{k-1} + \dot{v}_{k-1} \Delta t \\ \theta_k = \theta_{k-1} + \dot{\theta}_{k-1} \Delta t \\ \dot{v}_k = g \, cos\theta_k - \mu \Big[g \, sin\theta_k + \frac{v_k^2}{R}\Big] \\ \dot{\theta}_k = \frac{v_k}{R}}$

Run the algorithm until $\large{\theta = \frac{\pi}{2}}$ . The resulting final velocity comes out to be approximately $\boxed{1.37 m/s}$ .

The potential energy at rest at elevation R is dissipated as friction heat energy and is used to speed up the particle's speed (kinetic energy,) and the net difference is the work exhibited by the tangential force displaced R units. The centripetal force is only for changing direction and generates no work as it is normal on displacement.

Potential energy - Friction heat - Kinetic energy = Work of tangential force

cos(a)×PE - u sin(a)×PE - (2u/R)×KE = Ft×R

PE = potential E = m g R KE = Kinetic E = 0.5 m v^2 Fc = centripetal force R = radius of circle a = angle between radius & horizontal axis u = coefficient of friction m = mass Ac = centripetal acceleration = v^2/R v' = dv/dt = At = tangential acceleration Ft = tangential force = m At = m v'

Substitution:

cos(a) m g R - u sin(a) m g R - 2 u 0.5 m v^2 / R = m v' R

(Devide by R)

mg cos(a) - u mg sin(a) - u m Ac = m v'

mg cos(a) - u [mg sin(a) + m Ac] = m v'

Radial forces Fn = normal force = mg sin(a) + m Ac

Ff = frictional force = u Fn Fg = gravitational force = mg

Tangential forces Fg cos(a) - Ff = m At

Harout G. Vartanian - 4 years, 1 month ago

A rough slide

The answer is 1.37.

2 solutions

0 pending reports