Graphical Mechanics (Part 2)
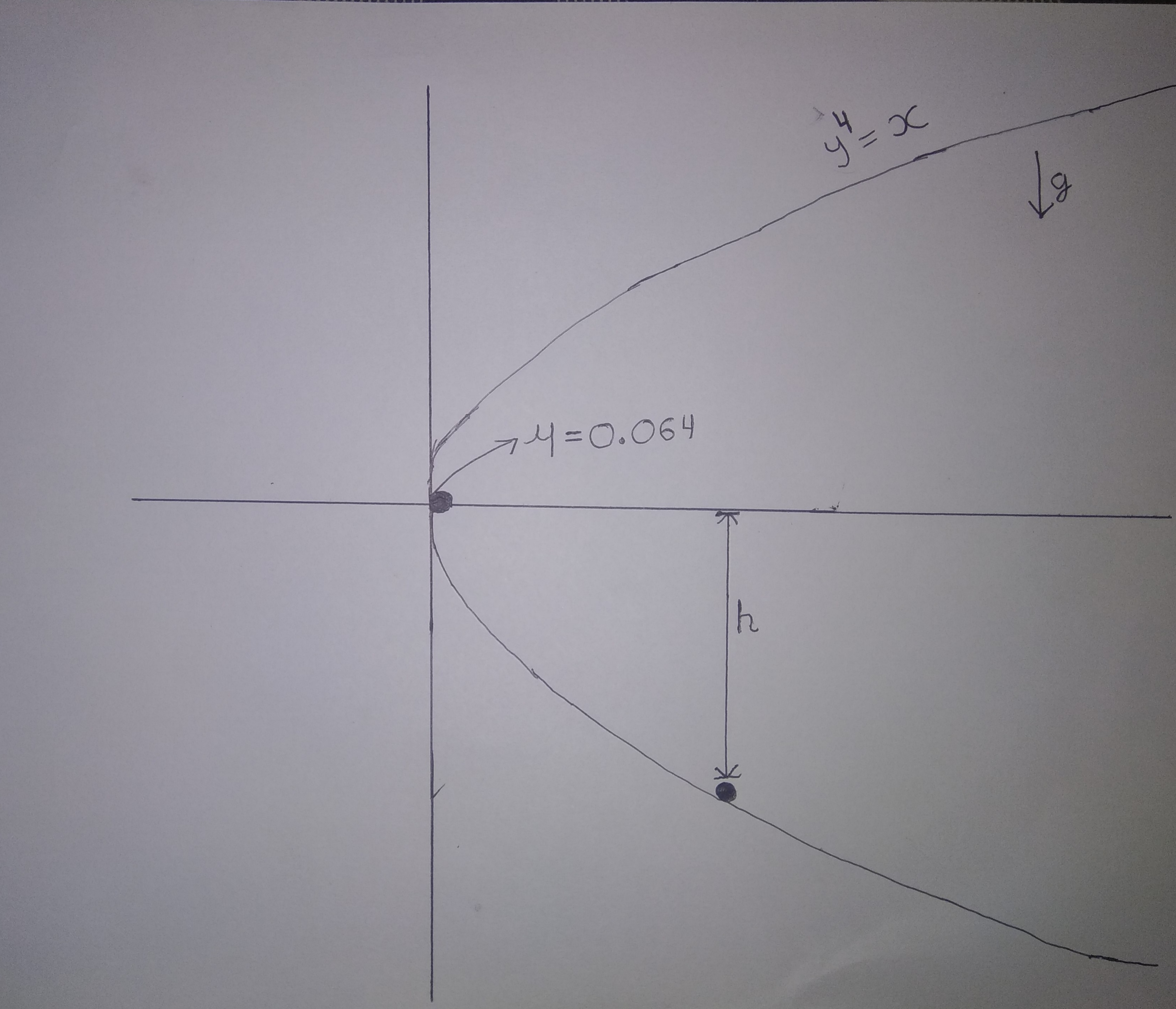
A particle of mass is released from on a shaped . After falling for time , it stops.
Enter value of in
Details and Assumptions
-
Take acceleration due to gravity
-
Coefficient of friction
Inspiration Aniket Sanghi
Try similar problem by me
All of my problems are original
The answer is 13.4868.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The position vector, velocity and acceleration of the particle are r = ( − y y 4 ) r ˙ = y ˙ ( − 1 4 y 3 ) r ¨ = y ¨ ( − 1 4 y 3 ) + 1 2 y ˙ 2 ( 0 y 2 ) and so the equation of motion of the particle (while slipping occurs) is m y ¨ ( − 1 4 y 3 ) + 1 2 m y ˙ 2 ( 0 y 2 ) = m R ( 4 y 3 1 ) − μ m R ( − 1 4 y 3 ) + m g ( − 1 0 ) and hence 1 2 y 2 y ˙ 2 ( 1 + 1 6 y 6 ) y ¨ + 4 8 y 5 y ˙ 2 = R ( 1 + 1 6 y 6 ) − 4 g y 3 = g − μ R ( 1 + 1 6 y 6 ) Eliminating R gives ( 1 + 1 6 y 6 ) y ¨ + ( 4 8 y 5 + 1 2 μ y 2 ) y ˙ 2 d y d [ 2 1 ( 1 + 1 6 y 6 ) e 2 μ tan − 1 ( 4 y 3 ) y ˙ 2 ] 2 1 ( 1 + 1 6 y 6 ) e 2 μ tan − 1 ( 4 y 3 ) y ˙ 2 = g ( 1 − 4 μ y 3 ) = g ( 1 − 4 μ y 3 ) e 2 μ tan − 1 ( 4 y 3 ) = g F ( y ) where F ( y ) = ∫ 0 y ( 1 − 4 μ u 3 ) e 2 μ tan − 1 ( 4 u 3 ) d u Thus the particle continues to move until it has dropped a depth h , where F ( h ) = 0 , and it takes time T = ∫ 0 h 2 g F ( y ) 1 + 1 6 y 6 e μ tan − 1 ( 4 y 3 ) d y to do so.
The rest is just numerical slog. With μ = 0 . 0 6 4 we obtain h = 2 . 4 5 9 4 0 9 8 7 8 and, with g = 1 0 , we obtain T = 1 3 . 4 8 6 8 .