From hot to cold and back again
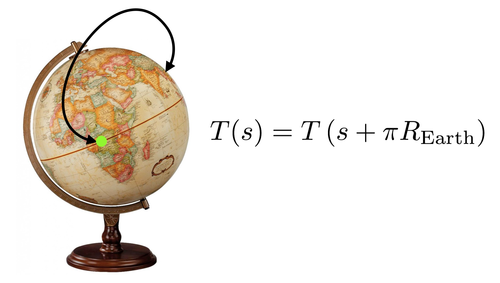 You're doing engineering work for an environmental organization, building a temperature sensing ring around the Earth, that can measure the temperature anywhere on the equator. While calibrating the system, you notice that there is
always
a point on the ring that has the same temperature as the corresponding point on the other side of the Earth. Is this a bug in the system?
You're doing engineering work for an environmental organization, building a temperature sensing ring around the Earth, that can measure the temperature anywhere on the equator. While calibrating the system, you notice that there is
always
a point on the ring that has the same temperature as the corresponding point on the other side of the Earth. Is this a bug in the system?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the temperature at the two sides of the Earth be T ( s ) and T ( s + π R ) . Their difference is f ( s ) = T ( s ) − T ( s + π R ) . Assuming temperature is continuous, f ( s ) is continuous.
Suppose that at the point s 0 , f ( s 0 ) = 0 . Without loss of generality, let us say it is positive at s 0 , i.e. f ( s 0 ) = T ( s 0 ) − T ( s 0 + π R ) > 0 .
If we move halfway around the equator to the new point s 1 = s 0 + π R , we have f ( s 1 ) = T ( s 0 + π R ) − T ( s 0 ) . However, this is equal to − f ( s 0 ) which is negative.
Because f ( s ) is continuous, the mean value theorem implies that f ( s ) must be equal to zero at some point s ∗ between s 0 and s 1 . However, that means that f ( s ∗ ) = T ( s ∗ ) − T ( s ∗ + π R ) = 0 , and therefore, the temperature at the two points is equal.
Of course, if we drop the starting assumption, that f ( s 0 ) = 0 , then f ( s 0 ) = 0 and we have found our point.
Please explain how the mean value theorem implies this
Log in to reply
So, MVT says that if some function g is continuous and g ( a ) = x , g ( b ) = y , and a < b , then for every z ∈ ( x , y ) there is some c ∈ ( a , b ) such that g ( z ) = c .
Since f ( s 0 ) > 0 and f ( s 0 + π R ) < 0 , there must be some s ∗ ∈ ( s 0 , s 0 + π R ) such that f ( s ∗ ) = 0 .
But when f ( s ∗ ) = 0 , T ( s ∗ ) = T ( s ∗ + π R ) . Do you see it now?
Log in to reply
A rather unexpected result!
Imagine the temperature graph of a point on the earth being a bit like a sine graph, regularly varying from a high to low point, in fact since the earth is circular and all the heat is from the sun, the output from your temperature sensor ring would look like the sine graph, with a high point on the bit facing the sun, and a low point on the bit facing away from the sun. The trap many people fall in to is thinking that the question means there is another high point, actually the two identical points are the two mid temperatures (think of the y=0 points on a 360 deg or 2pi rad section of a sine graph.) One of the points will be where it is going from day to night, and is cooling, the other point will be where it is going from night to day and is heating up.