From Twinkle Twinkle Little Star
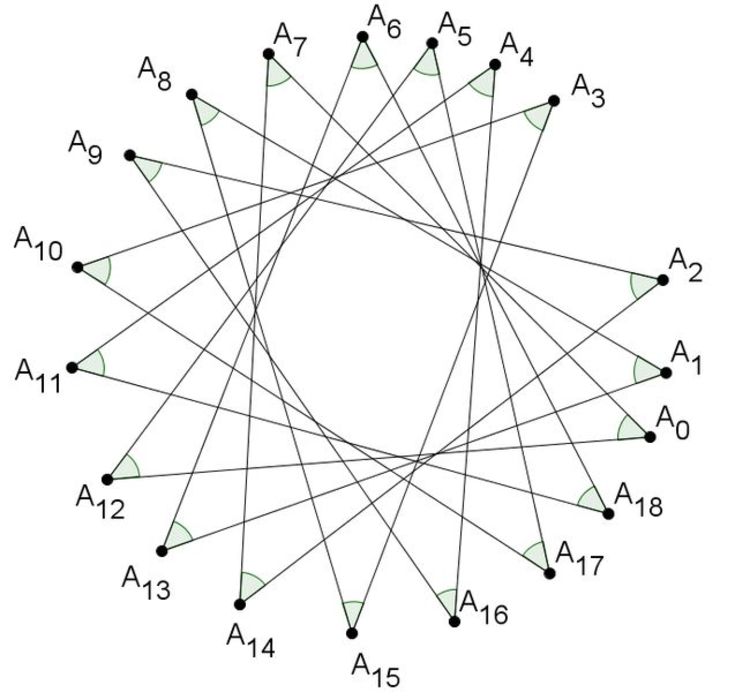 Find, in degrees, the sum of the marked angles.
Find, in degrees, the sum of the marked angles.
Remark : The above diagram consists of 19 points, A 0 , A 1 , … , A 1 8 , there are 19 line segments of form A i A i + 7 , where the subscripts read modulo 19.
The answer is 900.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Or you can just apply the formula: 1 8 0 ∘ n − 3 6 0 ∘ k , where n = 1 9 , k = 7 .
Log in to reply
An 8 lines or 8 vertices could have 3 6 0 ∘ while a 7 lines or 7 vertices could have only 1 8 0 ∘ . 5 times of 1 8 0 ∘ is a good question. A i A i + 7 gives k = 7 is not easy to determine to me.
Let the number of points be n , the angles equal to x i ∘ ( i = 1 , … , n ), and the number of times the figure turns around m .
In this case, n = 1 9 and m = 7 .
If you trace the figure, then at every angle x ∘ you turn ( 1 8 0 − x ) ∘ . Thus the total angle over which you turn is 1 8 0 n − i = 1 ∑ n x i = 3 6 0 m . Solving this gives i = 1 ∑ n x i = 1 8 0 n − 3 6 0 m . In this case, i = 1 ∑ n x i = 1 8 0 × 1 9 − 3 6 0 × 7 = 1 8 0 × ( 1 9 − 2 × 7 ) = 1 8 0 × 5 = 9 0 0 ∘ .
I don't think I have the same good sights as Chan Lye Lee. Here is my way:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
|
Sum of proximity gave 902. But I know it must be INT(902/ 180)*180, therefore it is equals to 900.
Answer: 9 0 0
Do you measure it by hand? It is not the intention, but you can always come with any method. Good try and good answer anyway!
Log in to reply
Yes. Otherwise there shall be no other possibility to me. The reason is features of whether 1 8 0 ∘ or 3 6 0 ∘ is not so direct and simple to add on without a careful study. Seems to be way dependent. I was taking no risk for a mistake.
Log in to reply
That is fine. As long as we are enjoying the problem solving.
Log in to reply
@Chan Lye Lee – We should enjoy problem solving.
Each of the '5-stars' and '7-star' is of angle-sum 180 degrees, which make the desired answer to be 900 degrees.