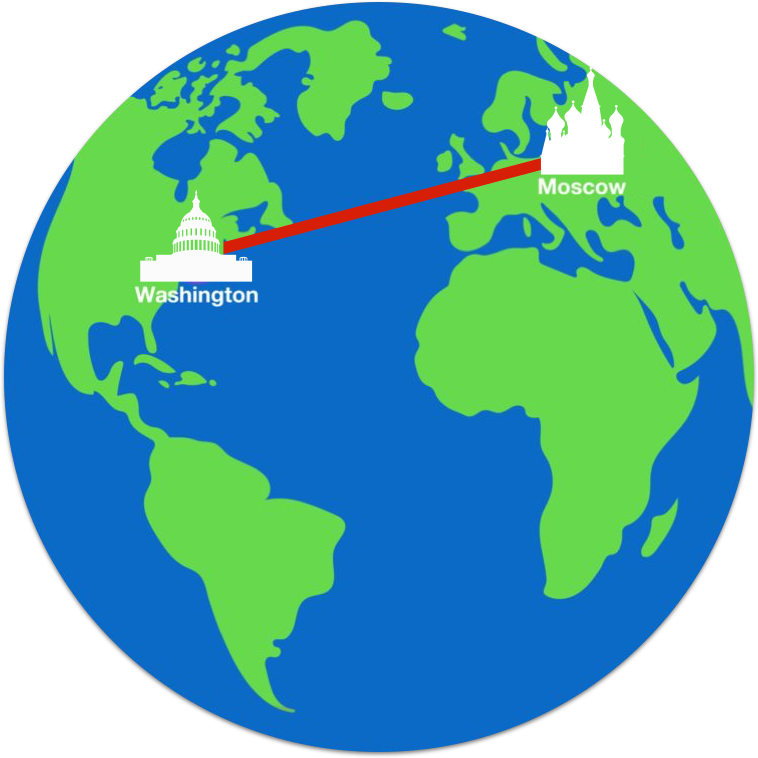
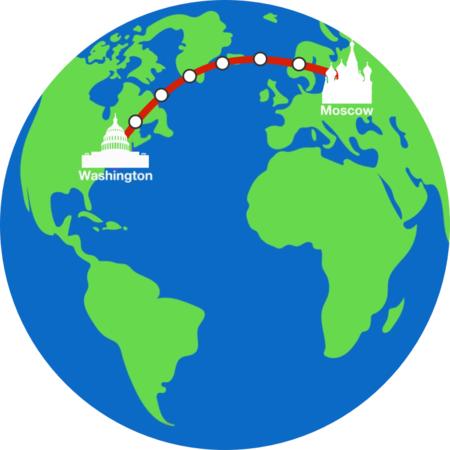
From Washington to Moscow
Which route (on Earth's surface) has a shorter distance?
Route A
Route B
Note: The images are a 2-D projection of the route on a globe, which is why the continents are in a slightly different shape. In particular, Greenland isn't as huge as compared to its representation using the cylindrical map projection.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Great visual!
To clarify, the top path with multiple stopping points corresponds to (an approximation of) my top path of a "straight line".
The bottom path with no stopping points corresponds to (an approximation of) my bottom path. E.g. you can see that it touches the tip of Greenland.
@Freyr Bergsteinsson How fitting that the shortest path passes right over Iceland!
This was not stated to be a map projection. It is just a circle with two points whose names happen to be the same as two cities on our globe. Therefore the straight line is the shortest line.
Log in to reply
I agree with you
Log in to reply
I agree too
I just know that on tv and in airports it’s always a curved line so I went with it.
the map in the question was not a map projection it was drawn as if it was a globe, in which case the straight line is shorter.
The question does not say to factor in the curvature of the earth therefore the distances are the same.
The perception of a trip such as the one illustrated in this problem is completely dependent on the type of map used. The world is basically spherical and a map is a 2 dimensional representation of the surface of that surface there is always some distortion in the perception of the surface. In reality the top route which appears to be a strait line on the map would be a complicated constantly turning rout across the surface of the earth. The lower route that appears to be a curved line on the map would be one continues straight line along the earths surface ie if this route was set with an aircraft there would be no requirement to turn for the entire trip
A number of years ago I did up a little graphical calculator which will calculate and display the travel distance between any two point chosen on the earths surface. It also calculates and displays the direction and distance of and imaginary trip straight though the earth directly between the two points on the earths surface. I am not sure what can be seen from this image
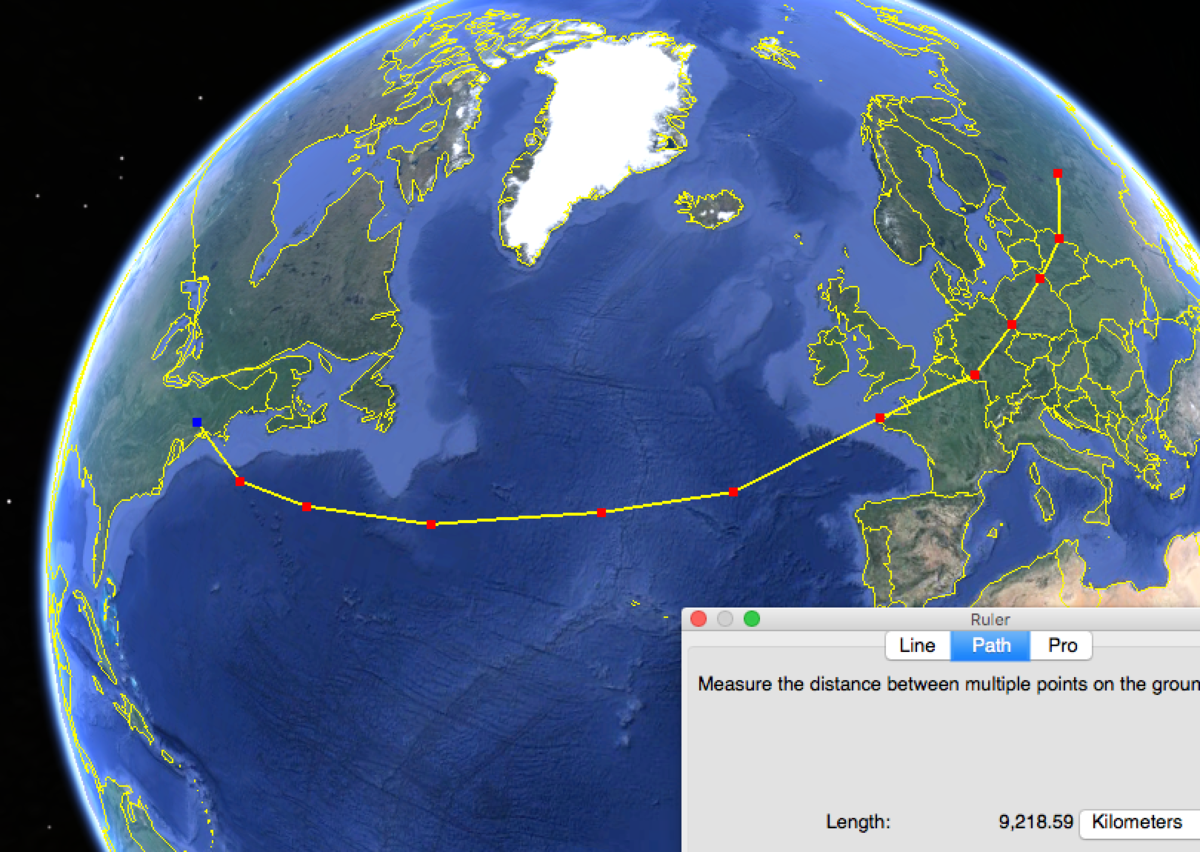
this screen shot but this is a trip from New York city to Moscow
Very nice calculator that you created! I'm curious, what was it for? Just a hobby?
Log in to reply
Yes, just something to give me a bit of a project one cold winter day. I have been interested in maps, charts, and projections for some time. I thought it might be interesting to have a simple quick calculator to indicate the shortest route over the surface of the earth. I was also intrigued by the idea of having the actual relative direction between locations on earth. Say I wished to point directly at Moscow through the earth where is it located? I find it somewhat unexpected how small the difference in the distance around the surface is compared to through the earth. Trips that cross the equator often look very strange as they curve in opposite directions north and south of the equator. I guess I have a lot of spare time some winter days??
Log in to reply
Indeed! The actual relative direction on Earth's surface as expressed on a 2-D map, is really confusing to think about. I only vaguely understood it, until I took a topology course on such map transformations and calculating distances through the coordinate maps.
Oh! That fact about "trips across the equator" would be really interesting! Could you post such a problem?
I guess I have a lot of spare time some winter days?
Haha, that's what happens when you live in Canada. I'm glad to be out of Chicago and not having to deal with their winter storms.
Log in to reply
@Calvin Lin – Well I am a grain farmer so winter has no field work for mouths. Just a lot of office work, highway travel with large trucks and spare time. If I remember I started of with a hand held calculator found it to tedious so switched to a spread sheet. Soon decided to download an incorporate the table of city locations around the world (longitudes and Latitudes). Then decided it would be nice to actually see the route and included a map, and have the option to pick locations with the mouse. it kind of evolved. As it is now it is done with MS Access and VBA code.
Chord and arc are almost the same when both are almost the same distance from the center of the earth.
It is unclear whether the circles represent a lace where one has to stop or a space above the circle!!!!
Log in to reply
I don't know if I understand what your comment is addressing. I did not have anything to do with the original problem but I will comment on what I believe is related to your comment. I assume you may be referring to the 6 white circles that are on the route B between Washington and Moscow. On a actual trip along the earths surface between Washington and Moscow taking the shortest possible distance, all of these points would be on that route. The circles could be thought of places along the route that the traveler will pass through.
The problem asks " Which route has a shorter distance?". In terms of distance it will not make any difference to the length of the trip if the traveler stops at these points or not, the distance will remain the same.
The earth is round, so if you check it on a globe, you'll see that the bottom one is indeed shorter (the illusion is achieved by orthogonally projecting earth's surface into 2 dimensions).
Yup, the bottom path is closer to that of a great circle from Washington to Moscow.
Log in to reply
How do you know that the path has a similiar curvature to that of the Earth?
Log in to reply
You do not know that it has a similar curvature to that of the Earth.
However, you can reason that it has a shorter distance, because the "horizontal distance" and the "vertical distance" is much smaller the higher you go up, thereby contributing to a much smaller total distance.
Shouldn't they have equal distance?
Log in to reply
Why should they have equal distance?
They have equal Displacement , but the distance travelled is likely to be different.
The geodesic(the shortest or longest path)between of two points on a sphere is a circumference of maximum radius, i. e, it's the circumference with center to be the center of the Earth passing through the two points on the sphere. In this case, it seems the bottom route, but I have some doubts...
Log in to reply
Remember that we also have a 2-D representation of a 3-D sphere. Points that are towards the top of the map are actually much more bunched together (e.g. Greenland is actually really small), and so the top route is actually pretty curved out, while the bottom route is much more of a straight line.
How can we know that it is, indeed, shorter? I mean, without have to look at a globe
Log in to reply
Since air lines will always take a short root unless the weather is bad. They take through green land not to show us green land. !
Given the question used dots in one route & not the other - one must assume given areas traversed they were breaks by aeroplane or boat. The non-dotted route is shorter in time as a result.
only in a flat world would a be the solution/ work it out on a balloon
I think if the path is under the surface of the earth, then straight path would have been the answer. ;)
As the earth is round the bottom route is a lot shorter . The shortest way between two points on earth is indeed a straight line but drawing a straight line between any two places would take us somewhere near the center of the earth. THAT'S CERTAINLY NOT POSSIBLE TO TRAVEL RIGHT NOW BY AN AIRCRAFT !!!
It all depends on the two locations. Say LA to Houston . It would straight.
I'm surprised no one has mentioned the equatorial bulge (or flattening/compression of the spheroid into a ellipsoid). Though the equitorial bulge only has a small effect on Earth in terms of distance traveled, presumably there is a measurable difference and so this would make the top route additionally slightly (a few miles?) longer -- because it is closer to the equator than the bottom route -- than were it on a spheroid Earth. It doesn't change the answer, but it is interesting to note that had the question been asked about travel between 2 points on Jupiter, the equitorial bulge would cause a noticeable addition to the miles traveled for a closer-to-equitorial route. Just musing.
That's a great question! Could you post that version? E.g. A "great circle" that goes about the equator more will be longer than a "great circle" that goes through the pole.
Closed geodesics do not need to have the same lengths, and it all depends on the topology of the surface.
Log in to reply
Calvin, when you say "post that version" are you suggesting that I publish a new geometry problem? If so, should I just post it similar to this problem (3 possible answers)? Thanks, Richard
Log in to reply
Yes, please publish a new problem.
I think a similar setup would work, where we have a (square) map of Jupiter and ask if the horizontal line or the vertical line has a shorter distance.
Log in to reply
@Calvin Lin – Thanks, Calvin. I posted the new Jupiter problem .
The Earth is round, and the path shown on the bottom is actually a straight line on a sphere when "unrolling" it into a planar shape. So, the bottom path is shorter.
I very much dislike this question. It is not a geometry problem as there is no easy way to verify which is shorter just by looking at the problem. Instead you need to actually find where the 2 locations are and compare the routes.
Route B could easily be presented going further north and not actually being a shorter route. All you can tell from this page is that route A is not going to be the shortest possible route, not that route B will be shorter.
My reasoning goes like this. In route A I'm moving on a "maximal circle" which is the result of intersecting the sphere with a normal plane. Route B lies instead on a circle that is not maximal, thus "shorter"
has any just put in the rotation of the earth
"[A] straight line is not the shortest distance between two points." - Charles Wallace, A Wrinkle In Time (Madeleine L'Engle, 1963)
The top route acording to me does not exist because it penetrates through the earth. So, the only one left is the top route. And earth is more spherical towards the equator and more flatter at the poles. And as the top route is not parallel to the equator, it is not a perfect semicircle.
How does it "penetrate through the earth"? You are travelling on the Earth's surface.
I don't think you understand this problem at all. We're not looking for "perfect semicircles". We are looking for "Great Circles" on the sphere. Yes, the earth isn't a perfect sphere, but thinking of great circles is a close enough approximation.
Log in to reply
So, is the top route the straight "land" way between the 2 places?
Log in to reply
The routes are on the surface of the earth, similar to what you would expect if someone traced a route on the map.
Log in to reply
@Calvin Lin – Oh! Now I get it so the answer is that the bottom route is shorter if we plot the whole route on x-axis and y-axis because of its spherical shape, right?
I read all the b solutions but I still don't get it. It just doesn't look right!!
Log in to reply
It requires you to realise that the initial diagrams are marked on a flat projection. Because they were shown as circles I made the mistake of assuming they were 2D representations of a line on a globe. I did that since Antarctica and Australia are not shown.
I don't know whether that will help you understand any better
That's because it's drawn wrong -- see my comment.
Route B CANNOT be a great circle as diagrammed. Projected onto the paper (drawing plane) as shown, the radius of any great circle must be >= the radius of the globe itself. (Try it!) As drawn the projection of Route B onto the paper clearly has a smaller radius than the globe. It cannot be a great circle--it goes way too far north! So, technically the problem is unanswerable. At best, the drawing is very misleading. I did not think to refer to an actual map of the earth to see where the great circle path would be (i.e., crossing Greenland where it does, etc.) That would be the only way to convince yourself that Route B is a great circle.
Technical correction: A great circle would project onto the paper as an ellipse. The part of the ellipse we see as Route B should approximate a circle with greater radius than the globe. Only when you get very, very close to the edge of the globe (where the "pointy" part of the ellipse is), would that projection approximate a circle with a smaller radius.
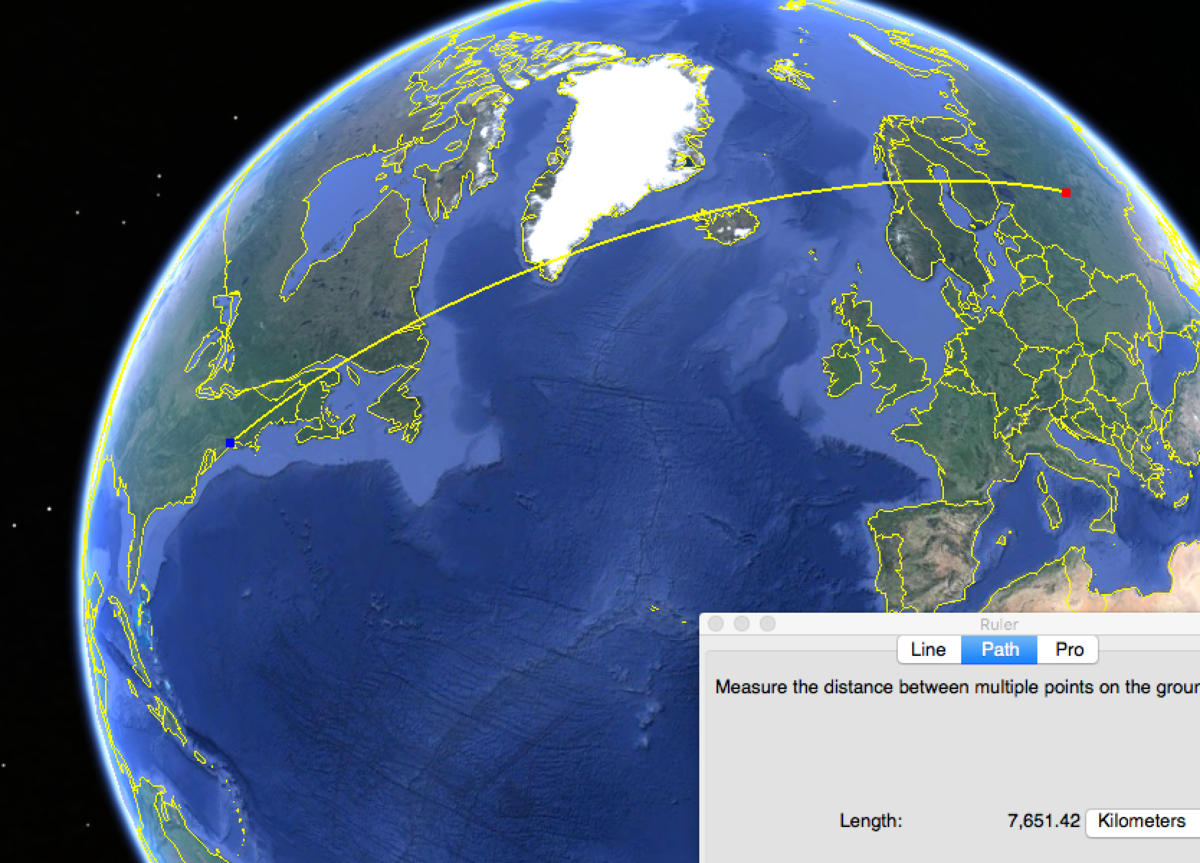
It can be hard to wrap our heads around the distortions that occur with map projections. Tracing these two paths on a globe gives us clear evidence of which route is shorter: