A geometry problem by A Former Brilliant Member
This annulus has been formed from two concentric circles. A chord of length t of the larger circle is then drawn tangent to the inner circle.
If you only know the value of t , can you calculate the area of the annulus?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Pythagoras, not Pythagorus
Log in to reply
Thanks, I corrected that
Log in to reply
Now you did phythagoras ;-)
Pythagoras or Pythagorus? Pythagoras was a Greek, so he would have spelled his name using the Greek alphabet. The common present-day spelling in the Latin alphabet, Pythagoras, is a phonetic version of the original. From this perspective, is Pythagorus any less correct?
But how do you prove that perpendicular drawn from center bisects t?
Log in to reply
In the original question it is stated that the chord line is tangent to the inner circle. A tangent is always perpendicular to the radius of that circle at the point of contact.
U can see that both the smaller right triangles are similar to each other. Both have same hypotenuse R , a common side r and same angle of 9 0 ∘ .
Hence, by SSA Congruence you can say the both have equal portion of the tangent t .
Log in to reply
And you might add that SSA congruence is only valid in right triangles, sometimes being referred to as HL or Hypotenuse Leg congruence.
If a radius is perpendicular to a chord then it bisects that chord.
So, as r approaches 0, t becomes the diameter of the outer circle and t/2 becomes R, it’s radius. Therefore A = pi*t^2/4? Hm.
Log in to reply
Yeah... Its quite interesting. You can try this on Desmos .
Since the diameter of the circles is not given, assume they do not matter and assume the diameter of the inner circle is zero. Thus t is the diameter of the outer circle.
Log in to reply
That actually wont be that satisfactory to directly ignore the radii of two circles. Since, I used the radii of thise circles to prove the question. If I had ignored them, I wouldn't be able to prove. It does work, but not always.
Think about the inner circle getting smaller and smaller, eventually the chord will become diameter.
⇒ R = 2 t
⇒ A = π × 4 t 2
If you sweep the chord around the circle, each half of it will cover the area. The area is therefore half t integrated over 2 pi.
Where in that do you use the fact that t is tangent to the inner circle?
Log in to reply
The tangent gives you a line that can be swept around the circle. The area of a shape is the length of a line covering one of the range integrated over the other range. If you look at the tangent it gives you two such lines from the inner circle to the outer one. Integrating either over 2 pi radians will get you the area.
Sorry - I don't understand this - what do you get when you integrate t/2 over 2pi ?
Log in to reply
Same here... I advise you to use LateX
Log in to reply
Sorry, on a phone :(
Log in to reply
@Paul Laws – Its okay but can you explain "half t integrated over 2 pi."
t/2 is a line from the inner circle to the outer one. Integrating this around the circle (0 to 2 pi radians) gives you the area of the shape.
That seems counter-intuitive to me. Interesting. Good work.
This particular method was suggested by a MIT student. Check this link .
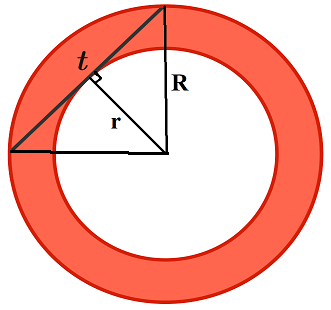
From the diagram, we deduce that t = 2 R 2 − r 2 ⟹ R 2 − r 2 = 4 t 2 . The area of the annulus is π R 2 − π r 2 = π ( R 2 − r 2 ) = 4 π t 2 .
You have no data except t and that the triangle has a 90d corner. This is not enough information to derive the other values.
Log in to reply
Using Pythagorean Theorem on one triangle (let the leg that is not a radius have length x ): x 2 + r 2 = R 2 ⟹ x = R 2 − r 2 . The same can be used on the other triangle (let the leg that is not a radius have length y ) : y 2 + r 2 = R 2 ⟹ y = R 2 − r 2 . Since t = x + y , this gives us t = 2 R 2 − r 2 , which is enough to find the area since the formula for the area of an annulus is only dependent on the differences of the squares of the radii.
Hopefully, that clarifies things.
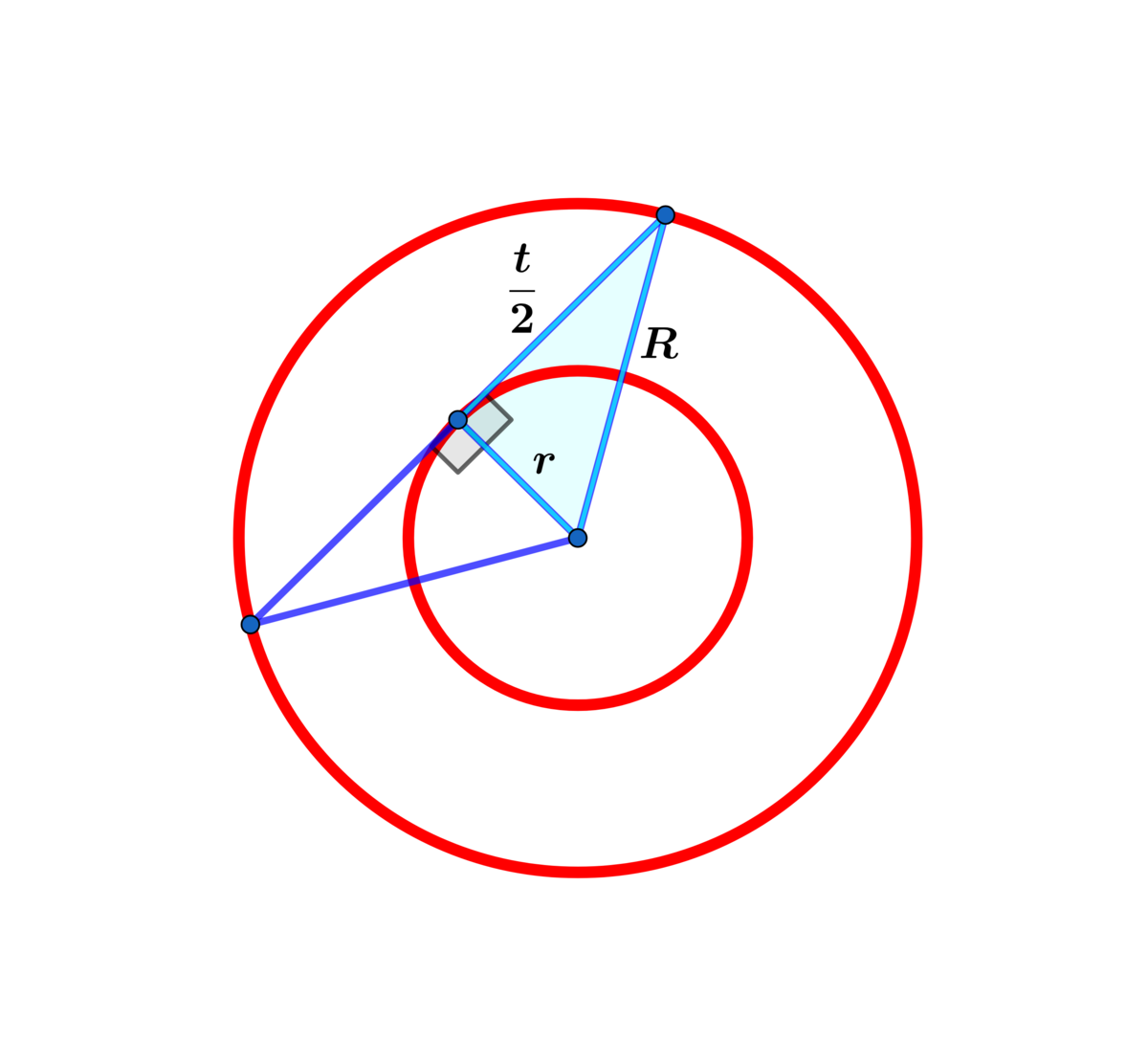
4 t 2 = R 2 − r 2 ⟹ A a n n u l u s = π ( R 2 − r 2 ) = π 4 t 2 .
This is a very popular problem and area is equal to a circle of diameter=t.
Similar problems exist in 3D shells also.
I don't understand. What is a "circle of diameter"?
Log in to reply
Intuitively I arrived at Vinod's solution. As we reduce the diameter of the inner circle toward zero, then t defines the diameter of the outer circle.
If R & r is the radius of bigger & smaller circles respectively, t=2√(R^2-r^2) The area of the annulus is π(R^2-r^2)=πt/2. So knowing t, the area will be known
If you can set a circle of radius 1 inside a circle of radius 2 and create a square tangent to radius 1 and radius 2. Then the squares sides will be the size of radius 2.
r = radius of small circle, R = radius of large circle. By pythagoras Theorem, R^2 - r^2 = (l/2)^2. Then pi*(R^2- r^2)= annulus area = pi(l/2)^2. Ed Gray
The length of the tangent specifies a unique pair of circles that satisfy the given conditions. If the circles are not identical, then their areas and the area the annulus they form can be calculated.
Now, Apply Phythagoras Theorem,
4 t 2 + r 2 = R 2
Hence we get, 4 t 2 = R 2 − r 2
Here, we can vary the radii R and r and there are infinity possibilities of such variations satisfying the above equation.
Now, Area of the Red Region ( A ) = Area of Annular Ring = (Area of Outer Circle) - (Area of Inner Circle)
A = π R 2 − π r 2 = π [ R 2 − r 2 ] = π 4 t 2
Hence, Area of Annular Ring is independent of radii of the two circles and depends only on the length of tangent.