Function can be tricky (3)
f ( x + x 1 ) = x 5 + x 5 1
f ( 3 ) = ?
The answer is 123.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
An easier method would be to find x such that x+1/x=3 and then just expand using bionomial theorm , it was really easy as some terms got cancelled out.
Log in to reply
Sorry, but I don't know how. I just wanted to show that it could be solved using Newton's sums method. I just did a spreadsheet and the answer came out.
Log in to reply
plz see my solution.
Log in to reply
@A Former Brilliant Member – Thanks. Read it but still don't know how. You need to learn up LaTex to present your solution.
Log in to reply
@Chew-Seong Cheong – i don't know how to apply latex but just wrote in daum equation editor as suggested by you.
Log in to reply
@A Former Brilliant Member – You can see the keystrokes by choosing by clicking the top-right pull-down menu button (next to "Level 4") Toggle LaTex and learn. You can also see the keystrokes by placing your mouse cursor up the formulas.
Let y = x + x 1 :
( x + x 1 ) 2 = x 2 + 2 ( x ) ( x 1 ) + x 2 1
x 2 + x 2 1 = y 2 − 2
x 3 + x 3 1 = ( x + x 1 ) ( x 2 − ( x ) ( x 1 ) + x 2 1 )
x 3 + x 3 1 = ( y ) ( y 2 − 2 − 1 )
x 3 + x 3 1 = y 3 − 3 y
( x 2 + x 2 1 ) ( x 3 + x 3 1 ) = x 5 + x 5 1 + x + x 1
x 5 + x 5 1 = ( y 2 − 2 ) ( y 3 − 3 y ) − y
x 5 + x 5 1 = y 5 − 3 y 3 − 2 y 3 + 6 y − y
x 5 + x 5 1 = y 5 − 5 y 3 + 5 y
⇒ f ( y ) = y 5 − 5 y 3 + 5 y
f ( 3 ) = 3 5 − 5 ( 3 ) 3 + 5 ( 3 )
f ( 3 ) = 1 2 3
Here's a solution reverse engineered from @TommyLi 's solution using simple polynomial division :
 Solution
Solution
y = x x 2 + 1 ⟹ f ( x + x 1 ) = f ( y )
f ( x x 2 + 1 ) = x 5 + x 5 1 = x 5 x 1 0 + 1 = ( x x 2 + 1 ) ( x 4 x 8 − x 6 + x 4 − x 2 + 1 ) =
= ( x x 2 + 1 ) ( ( x x 2 + 1 ) 4 − x 4 5 x 6 + 5 x 4 + 5 x 2 ) =
= ( x x 2 + 1 ) ( ( x x 2 + 1 ) 4 − 5 ( x x 2 + 1 ) 2 + 5 x 2 x 2 ) =
= y ( y 4 − 5 y 2 + 5 )
y = 3 ⟹ f ( 3 ) = 3 ( 3 4 − 5 ⋅ 3 2 + 5 ) = 1 2 3
(x+1/x)^5=(x^5+1/x^5)+5(x+1/x)^3-5(x+1/x) (Using binomial theorem) So,f(x+1/x)=(x+1/x)^5 - 5(x+1/x)^3 +5(x+1/x) Put x+1/x=3 So f(3)=243-135+15 =123
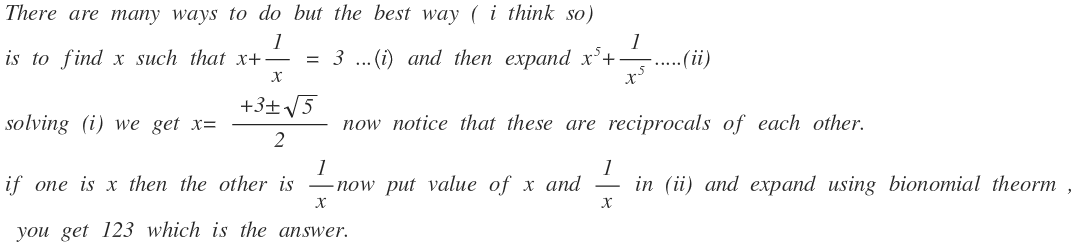
Since f ( x + x 1 ) = x 5 + x 5 1 , then if a + a 1 = 3 ⟹ f ( 3 ) = a 5 + a 5 1 .
The problem can be solved using Newton's sums method . Let P n = a n + a n 1 , S 1 = a + a 1 = 3 and S 2 = a ⋅ a 1 = 1 . Then we have:
\(\begin{array} {} P_1 = S_1 & \implies a + \dfrac 1a = 3 & = 3 \\ P_2 = S_1P_1 - 2S_2 & \implies a^2 + \dfrac 1{a^2} = 3\cdot 3 - 2 & = 7 \\ P_3 = S_1P_2 - S_2P_1 & \implies a^3 + \dfrac 1{a^3} = 3\cdot 7 - 1\cdot 3 & = 18 \\ P_4 = S_1P_3 - S_2P_2 & \implies a^4 + \dfrac 1{a^4} = 3\cdot 18 - 1\cdot 7 & = 47 \\ P_5 = S_1P_4 - S_2P_3 & \implies a^5 + \dfrac 1{a^5} = 3\cdot 47 - 1\cdot 18 & = 123 \end{array} \)
⟹ f ( 3 ) = 1 2 3