Functional Trigonometry
f ( θ ) = cot 2 θ + 1 ( cot 2 θ + 5 ) ( cot 2 θ + 1 0 )
Find the range of f ( θ ) for all real values of θ .
Wanna try more problems on functions?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
" f ( θ ) ≥ 3 ∗ 3 1 3 ∗ 3 6 = 2 3 . 2 9 1 8 . . . . . "
Shouldn't your minimum be 1 3 + 2 ⋅ 3 6 = 2 5 ?
And why is your boxed answer in an open interval? It should be [ 2 5 , ∞ ) .
Log in to reply
Thank you! The missed square bracket was just a careless typo, (are there any other kind?), but the messed up application of the AM-GM inequality was a certifiable brain cramp. :P Interesting though that when I included the constant I obtained a less stringent minimum. Anyway, I've made the appropriate edits; can I give you credit in my solution or just leave things as is?
Log in to reply
Equality only holds when all the terms are equal.
And it's easy to see that there's no maximum, so you can just stop at minimum is 25.
No credits necessary!
Log in to reply
@Pi Han Goh – Right; "Equality only holds when all the terms are equal" will be the phrase that keeps running through my head for the next little while. :) Thanks again.
Replacing c o t ( θ ) 2 with the variable x , we can graph the function and see the minimum value.
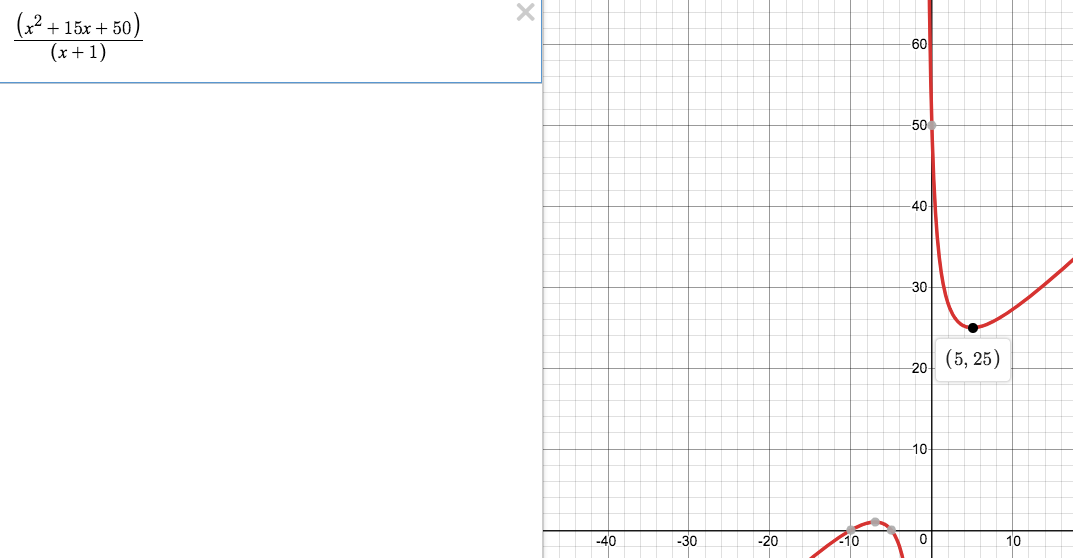
From the graph, the minimum value is 2 5 , when x = 5 . Since c o t ( θ ) 2 = x = 5 has a defined value of θ , the minimum value of the expression is 2 5 . c o t ( θ ) 2 can go till infinity, making the upper bound infinity.
write \superscript c o t θ 2 as x and since x must be positive solve algebraically since i think solving with calculus will be painful ! use the condition D >0 and get the answer !
Note first that cot 2 ( θ ) + 1 = csc 2 ( θ ) , and thus
f ( θ ) = csc 2 ( θ ) ( csc 2 ( θ ) + 4 ) ( csc 2 ( θ ) + 9 ) = csc 2 ( θ ) + 1 3 + csc 2 ( θ ) 3 6 .
Now since csc 2 ( θ ) has no upper bound (and is always ≥ 1 ), we know that the range of f ( θ ) goes to ∞ . For the minimum, by the AM-GM inequality we have that
f ( θ ) ≥ 1 3 + 2 ∗ csc 2 ( θ ) ∗ csc 2 ( θ ) 3 6 = 1 3 + 2 ∗ 6 = 2 5 .
This minimum can be achieved when csc 2 ( θ ) = 6 , and so the range of f ( θ ) is [ 2 5 , ∞ ) .
We could also use some calculus. Letting u = csc 2 ( θ ) , we find that
d θ d f = d u d f d θ d u = u 2 ( 2 u + 1 3 ) u − ( u 2 + 1 3 u + 3 6 ) ∗ ( − 2 ) ∗ csc 2 ( θ ) cot ( θ ) =
± u 2 ( u 2 − 3 6 ) ∗ 2 u u − 1 = ± u 2 ( u 2 − 3 6 ) u − 1 ,
where I brought in the fact that cot ( θ ) = ± csc 2 ( θ ) − 1 .
So the critical points, (noting that u = csc 2 ( θ ) ≥ 1 ,) are u = 1 and u = 6 .
At u = csc 2 ( θ ) = 1 the given function takes on the value 5 0 , (which turns out to be a local maximum), and at u = 6 the function takes on a value of 6 1 0 ∗ 2 5 = 2 5 . We can thus conclude that the range of the given function is [ 2 5 , ∞ ) .