Funny Fibonacci
The familiar Fibonacci sequence ( F n ) = ( 1 , 1 , 2 , 3 , 5 , 8 , … ) is defined recursively as F 0 = 1 , F 1 = 1 , F n = F n − 1 + F n − 2 for n ≥ 2 . Interestingly, F 2 5 = 1 2 1 3 9 3 and F 5 0 = 2 0 3 6 5 0 1 1 0 7 4 .
Now define a new sequence ( G n ) as follows: G 0 = 1 , G 1 = 2 , G n = 3 G n − 1 − G n − 2 for n ≥ 2 . Determine G 2 5 without using a calculator.
The answer is 20365011074.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The solution of the challenge appears to be: α k = L k , β k = ( − 1 ) k − 1 , where L n is the Lucas sequence, defined by the same recursion as the Fibonacci sequence but with different initial values: L 1 = 1 , L 2 = 3 , L n = L n − 1 + L n − 2 . Can anyone provide proof? I.e. show that in general F n k = L k F n k − k + ( − 1 ) k − 1 F n k − 2 k .
Log in to reply
consider the equation
F n + k + ( − 1 ) k F n − k = F n L k ⇒ ( 1 )
let us try proving this by induction
for k=1 it becomes
F n + 1 + ( − 1 ) F n − 1 = F n L 1 ,since L 1 = 1 it is valid
now lets assume its true for k=m,i.e.
F n + m + ( − 1 ) m F n − m = F n L m
now we meed to prove its true for n=m+1
F n + ( m + 1 ) + ( − 1 ) ( m + 1 ) F n − ( m + 1 ) = F n L m + 1
we have, F n + ( m + 1 ) = F n + m + F n + ( m − 1 )
and , F n − ( m + 1 ) = F n − ( m − 1 ) − F n − m
substituting these values in the LHS of the equation we get,
F n + m + F n + ( m − 1 ) + ( − 1 ) ( m + 1 ) ( F n − ( m − 1 ) − F n − m ) = ( F n + m + ( − 1 ) ( m + 2 ) F n − m ) + ( F n + ( m − 1 ) + ( − 1 ) ( m + 1 ) F n − ( m − 1 ) )
this can be slightly modified to obtain,
( F n + m + ( − 1 ) ( m ) F n − m ) + ( F n + ( m − 1 ) + ( − 1 ) ( m − 1 ) F n − ( m − 1 ) )
which by our assumption is equivalent to
F n L m + F n L ( m − 1 ) = F n ( L m + L ( m − 1 ) ) = F n L ( m + 1 )
thus it is proved by induction.
now in the above equation let n =p(q-1) and k=p ,we get
F p ( q − 1 ) + p + ( − 1 ) p F p ( q − 1 ) − p = F p ( q − 1 ) L p
on simplifying we get,
F p q + ( − 1 ) p F p ( q − 2 ) = F p ( q − 1 ) L q
or F p q = F p ( q − 1 ) L q + ( − 1 ) ( p − 1 ) F p ( q − 2 )
Log in to reply
Good ideas here.
Another approach would be to prove from the closed form of these numbers.
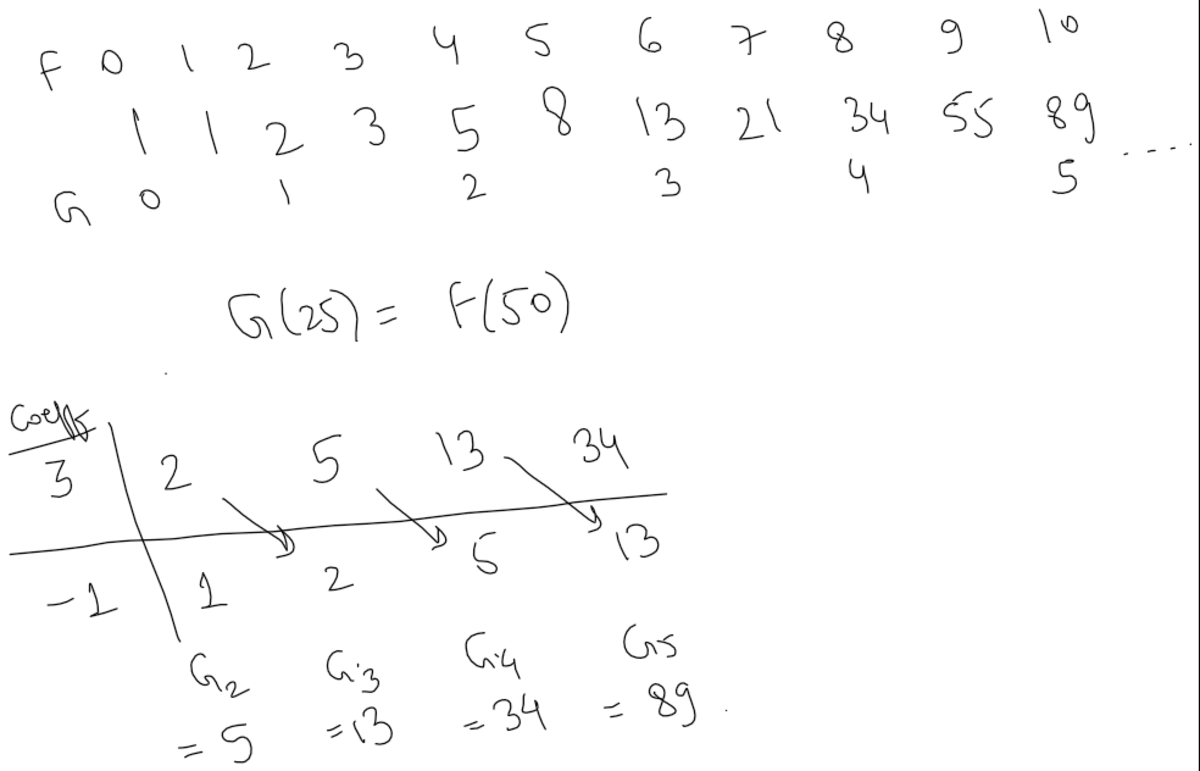
The trick is to notice that G n = F 2 n . It follows immediately that G 2 5 = F 5 0 = 2 0 3 6 5 0 1 1 0 7 4 .
Proof by induction: It is easy to see that G 0 = F 0 = 1 and G 1 = F 2 = 2 .
Induction step: Let n ≥ 2 , and suppose that we know G m = F 2 m for all m < n . Then G n = 3 G n − 1 − G n − 2 = 3 F 2 n − 2 − F 2 n − 4 = 2 F 2 n − 2 + ( F 2 n − 3 + F 2 n − 4 ) − F 2 n − 4 = 2 F 2 n − 2 + F 2 n − 3 = F 2 n − 2 + F 2 n − 1 = F 2 n .
Challenge : Generalize this. The recursion equation for the sequence ( G ( k ) ) defined by G n ( k ) = F k n has the form G n ( k ) = α k G n − 1 ( k ) + β k G n − 2 ( k ) . How can α k , β k be calculated? (For instance, α 3 = 4 and β 3 = 1 .)