Funny function
Consider a function f satisfying
f ( x ) = x 2 .
What is the value of f ( 2 ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
we need x equal to 5. with x < 16.2.
Log in to reply
let f( √x ) = x^2 be multiplied by x. and let f( t ) = z be divided by f( 2 ) then we have t = g( y ) = √y.
The function f( x ) = x 2 is of the form f( t ) = z which is composite where t = g( y ) = y and z = x 2 . Therefore , f( t ) = f( g( y ) ) = ( g ( y ) ) 2 = ( y ) 2 = y.
Given f( 2 ), then g( y ) = 2 and ( g ( y ) ) 2 = ( 2 ) 2 = 4
Log in to reply
We do not have f ( g ( y ) ) = g ( y ) 2 . If that were true, then f ( x ) = x 2 , but that is not what the problem stated.
It is not clear to me what your function substitution / composition is trying to achieve. Working with f ( g ( x ) ) = z ( x ) is often much more complicated.
Log in to reply
It should be f(g(y))=g(y)^4. Also y=x. It's wrong to say z=x^2 and t=sqrt(y) without saying y=x. With these two modifications, jonathan's answer would be correct, but still too complicated.
Log in to reply
@Nick Zafiridis – Right, my point is that we actually have f ( g ( y ) ) = g ( y ) 4 . It doesn't matter that he changed the variable from x to y .
Log in to reply
@Calvin Lin – He didn't change x to y though, he changed it to sqrt(y), right after saying z=x^2 and t=sqrt(y) without saying y=x. The latter is wrong, because it could lead to a misinterpretation like the former.
The square root of 1 is 1. 1 squared still equals 1. So, x = 1. 1 x 1 = 1. So, if the values of f and x are both one, then 2 x f is going to equal 2.
Log in to reply
Hm, I fail to understand what you are saying. Note that f ( x ) is a function , as opposed to the constant f multiplied by the variable x .
Log in to reply
@Calvin Lin – My bad. But, I doubt it will have any impact on the rotation of the earth - so, I'm not too worried.
The solution was way more easy...
A change of variable might help in transforming the function: Putting √ x = X we get, f ( X ) = X 4 Aah! We are familiar with this form, great.
⇒ f ( 2 ) = 2 4 = 1 6
SO much easier this way
Didn't got it
x = 2 ⇒ x = 4 ⇒ f ( 2 ) = ( 4 ) 2 ⇒ f ( 2 ) = 1 6
Both this one and the one at the top of the page (by Ariella Lee, who got the answer 4) seem correct, the one at the top seems more intuitive to me, but yours got the "correct" answer. I was wandering if there's something that I, and they, are missing.
Log in to reply
By reading Ariella Lee's solution, I gather she or he got the same answer. Not 4, but 16. Unless by answer 4 you mean the 4th answer, in which case Imran also got the 4th answer. To clarify, both Imran and Ariella conclude f(2)=16, which is the 4th and correct answer from the given choices.
I did the same procedure
Think of it as,
f
(
x
)
=
x
2
=
(
x
)
4
So,
f
(
2
)
=
2
4
=
1
6
And we're done...
Putting x = 4 ,
⟹ f ( 4 ) = 4 2 ⟹ f ( 2 ) = 1 6
You have to make the x^2 becomes something that has the same base as square root of x. So x^2=(x^1/2)^4, then subs 2 into x^1/2, then you will get 2^4=16 Hope you guys can understand. :)
That's correct! Thanks for sharing your approach. I have upvoted your solution. (+1)
The function f ( x ) is not defined for x. Thus, we need to make it into a function of a explicit input.
Assuming that x = t, we get x = t 2 . Plugging this in our function definition, x 2 = ( t 2 ) 2 = t 4 .
Now we just need to put our value and get 2 4 = 1 6 .
If it is given that f(\sqrt{x})=x^{2}
And we have, f(2)=f(\sqrt{4})=4^{2}=16
I got the answer correct and i love this society
f ( x ) = x 2 = f ( x ) = ( ( x ) 2 ) 2 = f ( 2 ) = ( ( 2 ) 2 ) 2 = ( 4 ) 2 = 1 6
My logic was as following, if we weren't inputed sqrt on the X we would have had a result of X to the 4th power,so, the function is powering the clean input (without square root) to the 4th power
Not sure how mathematically rigorous this is, but here is a graphical line of reasoning.
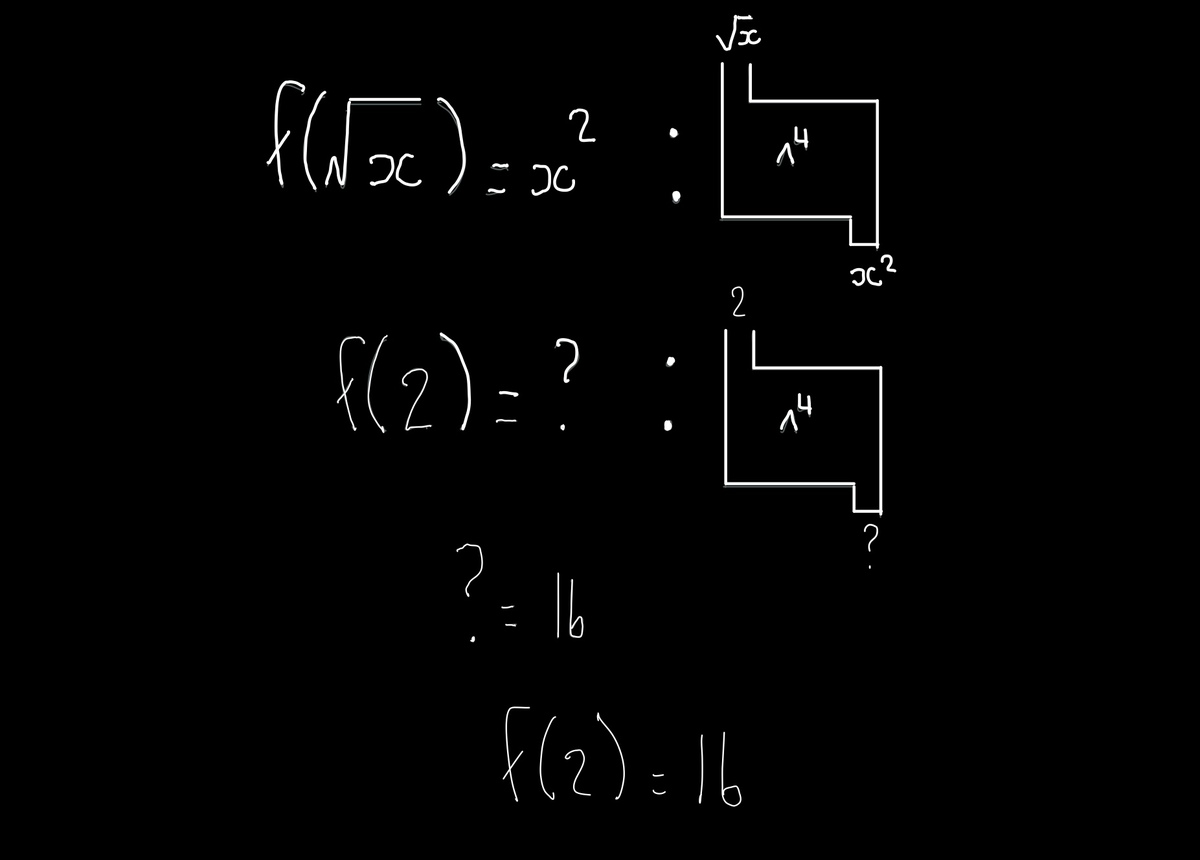
f ( x ) f ( u ) f ( 2 ) = = = x 2 , u = l e t x ⇒ x = u 2 ( u 2 ) 2 = u 4 2 4 = 1 6
so all we got to do is substitute 4 as, x^(0.5)=2 x=4. this gives us f(x)=x^2=4*4=16
f ( ( x ) ) = x 2 ⟹ f ( x ) = x 4 ⟹ f ( 2 ) = 2 4 = 1 6
Se f(2) então x^(1/2)=2, x = 2² Assim, x = 4 f(x^(1/2)) = x², portanto f(2) = 4² f(2) = 16
substitute the value of 2 as root x,now the answer will be x square....the value of x is one and only 4so the value of x square is 16 which is the answer...
Don't BS the students. Just tell them to find, mentally, a value of x so that it's sqare root Is 2.
Can we. Do like that
If f(√x)=x^2
Then f(x)=x^4
Then x=2 so and will be 16
Please correct me if iam wrong
YOU ARE TOTALLY WRONG............................................
ADD GOOD SOLUTIONS
F(√x)=x^2 here √4 is √x so x^2=16
The input of the function is not x . The input of the function is x .
Find the value of x needed to make 2 the input, i.e. set 2 equal to x .
x = 2 ( x ) 2 = 2 2 x = 4
To have an input of 2 , x must equal 4 .
f x ) = x 2 f ( 4 ) = 4 2 f ( 2 ) = 1 6