Fuss-ional Bicentric Integral Quadrilateral
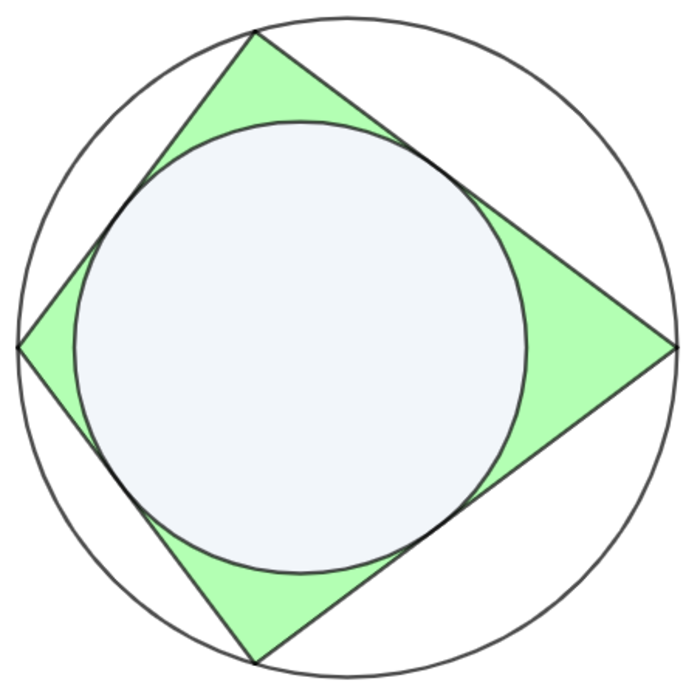
In the circumcircle of integer-valued radius , the bicentric quadrilateral whose side lengths are all integer-valued - each of them less than - and whose inradius is also integer-valued contains both integer-valued area (green and light blue inclusive) and integer-valued perimeter . In addition, the shortest distance between the circumcenter and the incenter is also integer-valued .
If are positive integers and , input as your answer (without the ).
The answer is 2607.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Some equations for a bicentric quadrilateral with sides a , b , c , and d include:
a + c = b + d
A = a b c d
P = a + b + c + d
r = a + c a b c d = P 2 A
R = 4 1 a b c d ( a b + c d ) ( a c + b d ) ( a d + b c ) = 4 A ( a b + c d ) ( a c + b d ) ( a d + b c )
d = x = R 2 + r 2 − r 4 R 2 + r 2 (Fuss' Theorem)
The following computer program brute forces every possibility for 0 < a < 1 0 0 , a ≤ b < 1 0 0 , b ≤ c < 1 0 0 , c ≤ d < 1 0 0 and finds that the only set with integer solutions is a = 4 2 , b = 4 2 , c = 5 6 , d = 5 6 , A = 2 3 5 2 , P = 1 9 6 , r = 2 4 , R = 3 5 , x = 5 , and r + R + A + P = 2 6 0 7 .