Galloping Queens #3
Define a Galloping Queen as a chess piece whose legal move is that of a Knight , and that of a Queen .
What is the minimum value of integer such that you can place non-attacking Galloping Queens on an chessboard?
Try more questions on Galloping Queens
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
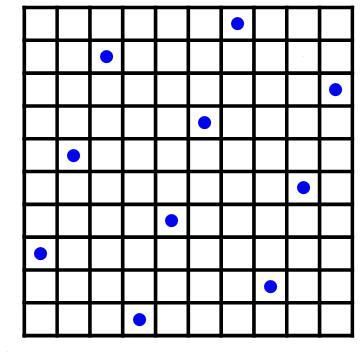
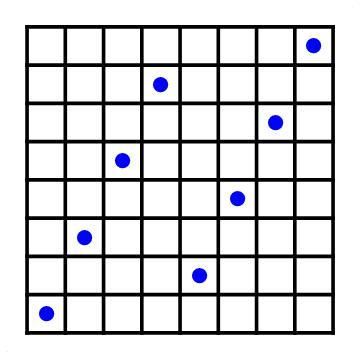
It is possible with 10 Galloping Queens:
This is actually the only arrangement, if you don't count rotations and reflections as new instances (otherwise there are 4).
Using a brute-force search it is also possible to exclude n ≤ 9 as possible options. Note that all solutions to the "n Galloping Queen problem" must also be solutions to the "n Queen problem", which has been very well studied. This means that a brute-force search in this case can be done by studying all known solutions and checking whether there are no knight moves between queens. There are e.g. only 46 fundamental solutions for the 9-Queen problem, so the required effort is small enough that you could check them by hand. And by the list of multiple choice answers for this problem, you can easily exclude n < 9 as these are not even given as options.