Garfields's hexagon
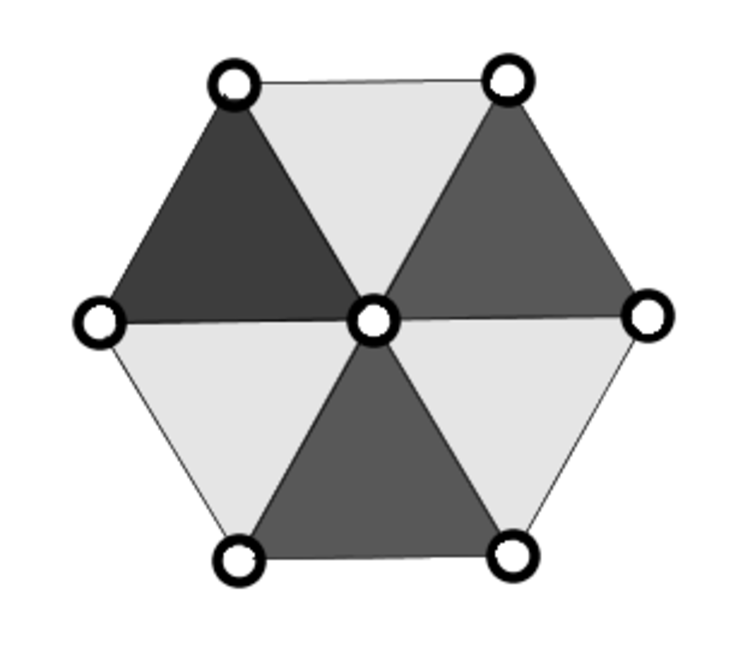 Garfield arranges the integers from 1 to 7 (inclusive) in the little circles of the hexagon above such that all shaded triangles have the same sum.
Garfield arranges the integers from 1 to 7 (inclusive) in the little circles of the hexagon above such that all shaded triangles have the same sum.
How many (distinct) arrangements are there?
The answer is 144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First find which numbers will be common for all shaded triangles (center circle) so the remaining numbers can be ordered in three pairs with the same sum.
If I put 1 ⇒ 2 + 7 = 3 + 6 = 4 + 5
If I put 2 there's no a possible arrangament
If I put 3 there's no a possible arrangament
If I put 4 ⇒ 3 + 5 = 2 + 6 = 1 + 7
If I put 5 there's no a possible arrangament
If I put 6 there's no a possible arrangament
If I put 7 ⇒ 1 + 6 = 2 + 5 = 3 + 4
So in the center I can put 3 numbers, then I select one number for the first saded triangle ( 1 6 ) , then by the second ( 1 4 ) and last by the third ( 1 2 ) . Result is 3 × ( 1 6 ) ( 1 4 ) ( 1 2 ) = 7 2 .
Note: I only select one number by triangle because the other one is definite by the first.