Gas Tank

Let's consider the problem in two phases phase 1, So let's start with 100% of the tank divided by 2 = 50% Then the tank is filled again to 100% but we have 50% old and 50% new gas, phase 2, remove a quarter from the full gas but so we need to take 12.5% from both because the liquids are equally mixed, 50% - 12.5% = 37.5%

Relevant wiki: Setting Up Equations

In the diagram below, the red area represents the original gas, the blue area represents the new gas from Step 3, and the green area represents the new gas from Step 5.

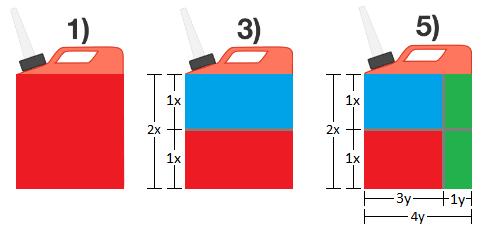
After the third step, half the tank is original gas and the other half is new gas, at a $1:2$ ratio, which is represented as a height of $1x$ out of $2x$ . After the fifth step, a fourth of both the original and new gas changes to new gas, at a $1:4$ ratio, which is represented as a width of $1y$ out of $4y$ .

The original gas has an area of $1x \cdot 3y = 3xy$ and the total gas has an area of $2x \cdot 4y = 8xy$ . The percentage is $\frac{3xy}{8xy} \cdot 100 = \boxed{37.5}$ %.

Relevant wiki: Multi-step Equations - Basic

Let total amount of gas the tank can hold be equal to ‘x’. Then , the original amount of gas (gas at the start of step 1) at the following steps is -

Step 1-> x

Step 2-> $\frac{x}{2}$

Step 3-> $\frac{x}{2}$

Step 4-> $\frac{3x}{8}$ Since the gases are mixed perfectly

Step 5-> $\frac{3x}{8}$

Now, percentage of the original gas in step 5 = $\frac{3}{8}\times 100 = \boxed{37.5}$ %

$0,5\cdot 0,75 = 0,375 = \boxed{37,5 \%}$

After step 1, all of the tank is original.

After step 2, when you used half the tank, half of the tank is original.

After step 3, when you filled the tank, half of the tank is still original.

After step 4, when you used $\frac{1}{4}$ of what remained, $\frac{3}{8}$ of the tank is original.

After step 5, when you refilled the tank, $\frac{3}{8}$ of the tank is still original.

$\frac{3}{8}$ = .375 = 37.5%

You start off with 100% original gas. You pour off half of that gas and fill it with new gas, giving you a mix (in this scenario every sample of gas taken from that container would have equal concentration of new and old) of \1}{2} new and $\frac{1}{2}$ original. You pour off a quarter of that mix, half of it being original. You poured off $\frac{1}{8}$ of a container of gas, meaning $\frac{3}{8}$ of a container is still original. Decimal form of $\frac{3}{8}$ is 0.375=37.5%

I originally assumed the OP was, that the process was repeated. Then the answer is as follows. Suppose stage 2n+1, the proportion of original petrol (‘gas’ is not a liquid—this term makes no sense!) be $p_{n}$ . Then $2^{-n}$ from the liquid is removed. This leaves a volume of $1-2^{-n}$ , so that when new petrol is added to fill the take, the proportion is $p_{n+1}=(1-2^{-n})\cdot p_{n} + 2^{-n}\cdot 0=(1-2^{-n})\cdot p_{n}$ . Clearly, $p_{0}=1$ , hence the general expression is

$p_{n}=\prod_{1\leq k\leq n}(1-2^{-k})$

and the ‘final’ proportion of original petrol (if at all a sensible value) must be of the form

$p=\lim_{n\to\infty}p_{n}=\prod_{k\geq 1}(1-2^{-k})$

Numerical simulations seems to point to convergence to approximately $\fbox{\$0,288788095086602\ldots\$}$ . Mathematically, the infinite product is provably convergent, since, taking logarithms, $\sum_{k\geq 1}\log(1-2^{-k})$ converges absolutely by the squeezing-lemma, since $0≤-\log(1-2^{-k})\leq 2^{-k}$ and $\sum_{k\geq 1}0$ and $\sum_{k\geq 1}2^{-k}$ both converge.

A nice closed expression for this product eludes me at the moment (it’s NOT $\zeta(2)$ nor $1/\zeta(2)$ , etc). For example taking logarithms yields $\log(p)=\sum_{n\geq 1}\sum_{k\geq 1} \frac{2^{-nk}}{k}$ . Swapping the sums (check if this is allowed! … it is by absolute convergence) yields $\log(p)=\sum_{k\geq 1}\frac{1}{k}\frac{1}{2^{k}-1}$ . But then I don’t see a simplification. Anyway, here’s a challenge for someone to think about.

We start with 100% of the gas. Then, half is removed meaning only 50% is left. Then, it is filled again which means 50% of the gas in the full gas (Step 3) is originally from step one. Then ¼ of the gas is taken out again. Because of this perfect mixing, take ¼ out of the 50% of the original gas.

½ x ¼ = ⅜

Now we have ⅜ of the original gas. Because it is filled up, then the value doesn’t change because none of it was the original gas. Therefore, ⅜ of the gas was left or 37.5% was still left.

Step 2 = 50% original gas. Step 4 uses 25% of the tank, half of which is the original gas so 12.5% is used of the original gas. 50%-12.5% = 37.5%

This problem should include that when you're filling the gas tanks, you're filling them with a substance other than gas. At first I wrote 100% as the answer, but then realized it was 37.5%.

Temporarily, disregard steps 3 and 5.

1) Start with full tank.

2) Use half the gas. (Now we are at 50%).

4) Use a quarter of the gas. Proportionally, we are using one quarter of the original gas left in the tank. You could also think of this step as using a quarter of the original gas and a quarter of the new gas from step 3.

Remaining gas is equal to 0.5 - (0.25*0.5) = 0.375

Step 5 can be completely disregarded since it adds only new gas and has no change on the original gas.

Removing gas will change the volume of original gas, but not the percentage. Adding gas will change the percentage of original gas, but not the volume.

For this reason, the percentage of original gas is 100% in both tanks 1 and 2. The volume of original gas in tank 2 is a one-half gallon. In tank 3, the volume of original gas is also one-half gallon (50%).

Tanks 3 and 4 both have 50% original gas. Since half of the gas in tank 4 is original, we can calculate that the volume of gas in the fourth tank is $\frac{3}{4}\div 2 = \frac{3}{8}$ gallons. Therefore, this is the volume of gas in the last tank. The answer is $\frac{3}{8} = \boxed{37.5\%}$ .

In 1st and 2nd step, concentration of originally is 1, but there just $\frac{1}{2}$ gas in step 2. At 3rd and 4th step, concentration is $\frac{\frac{1}{2}}{1}=\frac{1}{2}$ because we Assume perfect mixing, but there just $\frac{3}{4}$ gas in step 4. At 5th step, concentration is $\frac{\frac{1}{2} \times \frac{3}{4}}{1}=\frac{3}{8}$ ,and there have 1 gas, so the ratio of $m_{after}$ and $m_{before}$ = $\frac{\frac{3}{8} \times 1}{1}=\boxed{37.5}$ %.

Let's use the stages 1 to 5 to solve this problem. 1. In stage 1 the tank is full, that means 100% of the 'old' gasoline. 2. In stage 2 half of it was used, that means 50% of the ''old' gasoline. 3. In stage 3 it is refilled, so that is 50% 'old' and 50% 'new gasoline. 4. In stage 4 , 1/4th is used, so 75% of the total gasoline is left; 37.5% 'old' and 37.5% 'new' 5. In stage 5 it is refilled, so there is 37.5% old and 62.5% new gasoline. The question is 'What percentage of the gas in the tank after step (5) was originally there in step (1)?' so that is 37.5%.

50% x 75% = 37.5%

Assume gas tank volume being 100L. By step 2, 50L of the original gas remains. Assume perfect mixing in step 3, by step 4, 25% of the original gas and gas refilled in step 2 has been used. So the amount of the original gas remaining in the tank is 75% multiply by 50L. Since we had assumed that the tank volume is 100L, we can then deduce that the remaining gas comprises of 37.5% of the original gas.

If you swap the percentage against a volume the Solution becomes quite easy. 1) 100ml original fluid 2) 50ml original fluid 3) still 50ml original and 50ml new 4) you take a quarter away -> 50-50/4 = 37,5 original and 50-50/4 = 37,5 new 5) you fill up to 100 and your original stays the same -> 37,5

Start with a tank with 8/8 litres of petrol: x x x x x x x x

then 50%: x x x x

fill up with new petrol: o o o o x x x x

remove 25%, because 25% of 8 is 2, take 1 from both o and x leaving: o o o x x x

Fill up with new petrol: o o o o o x x x

now only 3/8 of the original petrol is remaining, this is equal to 37.5%

$Let's\ say\ we\ start\ with\ 8x\ litre\ of\ gas.\\ Step\ 1 = 8x\\ Step\ 2 = 8x - 4x\\ Step\ 3 = 4x\\ Step\ 4 = 4x-x\\ Step\ 5 = 3x\\ Thus,\ we\ are\ left\ with=\frac{3x}{8x}\times 100\%=\frac{300}{8}\%=37.5\%$ \

Consider the tank has a specific volume, eg. 1000 mL.

In the second step, half or 500 mL is used so 500 mL of old gas remains when the tank is refilled with new gas.

In the fourth step, a quarter or 250 mL is used which is equal parts or 125 mL each of the old and new gas.

500 mL - 125 mL = 375 mL of old gas remains once the tank is filled again or 37.5% of the original volume.

There is ¾ of ½ a tank of the original fuel left,

¾ × ½ = 3∕8 = 37.5%