Gauss Returns!

$S=0.1+0.02+0.003+0.0004+\ldots\\ 10S=1+0.2+0.03+0.004+\ldots\\ -S=-0.1-0.02-0.003-0.0004\ldots\\ 9S=1+0.1+0.001+0.0001+0.00001+\ldots\\ \text{The above is in geometric progression where } a_1=1, r=\dfrac{1}{10}\\ \text{Therefore as GP tends to infinity}\\ 9S=\dfrac{a_1}{1-r}\\ 9S=\dfrac{1}{1-\dfrac{1}{10}}\\ 9S=\dfrac{1}{\dfrac{10-1}{10}}\\ 9S=\dfrac{10}{9}\\ S=\dfrac{10}{81}\\ \text{Therefore the answer is 10 + 81 = }\fbox{ 91 }$

$\text{There are Millions of methods to solve this question, I think this is the simplest }$

$S=0.12345\cdots \quad \quad \small\text{ 1st Equation } \\ 10S=1.23456\cdots \quad \quad \small \text{ 2nd Equation } \\ \text{Subtract the two equations } \\ 9S=10\times 0.1111\cdots \\ S=\dfrac{10}{9} \times \dfrac{1}{9} = \dfrac{10}{81}$

$S= 0.1 + 0.02 + 0.003 + 0.0004 + ...$

$S= (0.1) + 2(0.1)^2 + 3(0.1)^3 + 4(0.1)^4 + ...$

Let $x=0.1$ , then:

$S = x + 2x^2 + 3x^3 + 4x^4 + ...$

$S = x + 3x^2 - x^2 + 4x^3 - x^3 + 5x^4 - x^4 + ...$

$S = x + (3x^2 + 4x^3 + 5x^4 + ...) - (x^2 + x^3 + x^4 + ...)$

$S = x + ( \frac{d}{dx} x^3 + \frac{d}{dx} x^4 + \frac{d}{dx} x^5 + ...) - (x^2 + x^3 + x^4 + ...)$

$S = x + \frac{d}{dx} (x^3 + x^4 + x^5 + ...) - (x^2 + x^3 + x^4 + ...)$

Since $x=0.1$ , both $x^3 + x^4 + x^5 + ...$ and $x^2 + x^3 + x^4 + ...$ are infinite geometric progressions. $(|r|=0.1<1)$ . Hence:

$S = x + \frac{d}{dx} (\frac{x^3}{1-x}) + \frac{x^2}{1-x}$

$S = \frac{x}{(1-x)^2}$

$S = \frac{0.1}{(1-0.1)^2} = \frac{10}{81} \implies \boxed{a+b = 91}$

We have,

$~~~~~~~~~~S = \dfrac{1}{10} + \dfrac{2}{10^{2}} + \dfrac{3}{10^{3}} + \cdots \infty \\ ~~~- \dfrac{S}{10} = ~~~~~~~~~~ \dfrac{1}{10^{2}} + \dfrac{2}{10^{3}} + \dfrac{3}{10^{4}} + \cdots \infty~~~~~~~~~~~~~~~~~~~~~~ \color{maroon}{\small\text{Shifting each term one place to the right}} \\ \text{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_} \\ ~~~~~~~~ \dfrac{9S}{10} = \dfrac{1}{10} + \dfrac{1}{10^{2}} + \dfrac{1}{10^{3}} + \dfrac{1}{10^{4}} \cdots \infty \\ \text{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_} \\ \Longrightarrow \dfrac{9S}{10} = \dfrac{\frac{1}{10}}{1-\frac{1}{10}} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \color{#302B94}{\boxed{\text{Using}~~ S_\infty = \dfrac{a}{1-r}, ~~{where}~~ |r|<1}} \\ \Longrightarrow \dfrac{9S}{10} = \dfrac{1}{9} \\ \Longrightarrow S = \dfrac{10}{81} = \dfrac{a}{b} \\ \therefore a=10 ~~~ \text{and} ~~~ b=81$

Hence, $a+b=\boxed{91}$

We have to find:

$\implies \dfrac{1}{10}+\dfrac{2}{100}+\dfrac{3}{1000}+ \ ...$

Using Arithmetic-Geometric progression .

$\implies \left(\dfrac{1}{10}\right)\left(1+\dfrac{2}{10}+\dfrac{3}{100}+ \ ...\right)$

Here $a=1$ , $d=1$ and $r=\dfrac{1}{10}$ .

$=\left(\dfrac{1}{10}\right)\color{#20A900}{\left(\dfrac{1}{1-\frac{1}{10}}+\dfrac{1×\frac{1}{10}}{\left(1-\frac{1}{10}\right)^2}\right)}$

$\implies \dfrac{1}{10}×\color{#20A900}{\dfrac{100}{81}}=\dfrac{10}{81}$

$\therefore a+b=10+81=\color{#BA33D6}{\boxed{91}}$ .

I tried a telescoping series approach on a finite version of the sum then applied the limit as k approaches infinity:

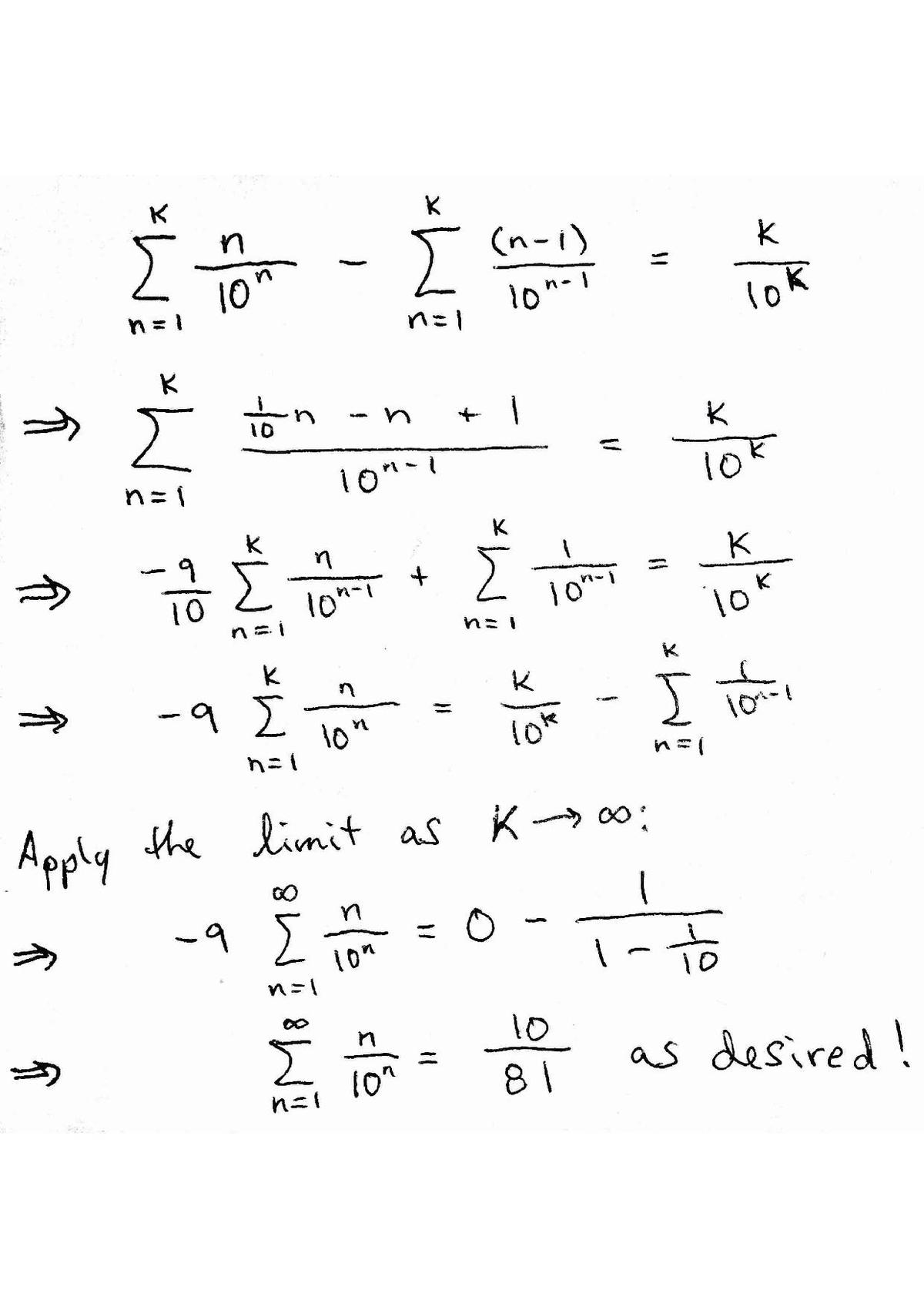
So, the sum a+b is 91.