Gauss's Law Exercise (part 5)

Electricity and Magnetism Level pending

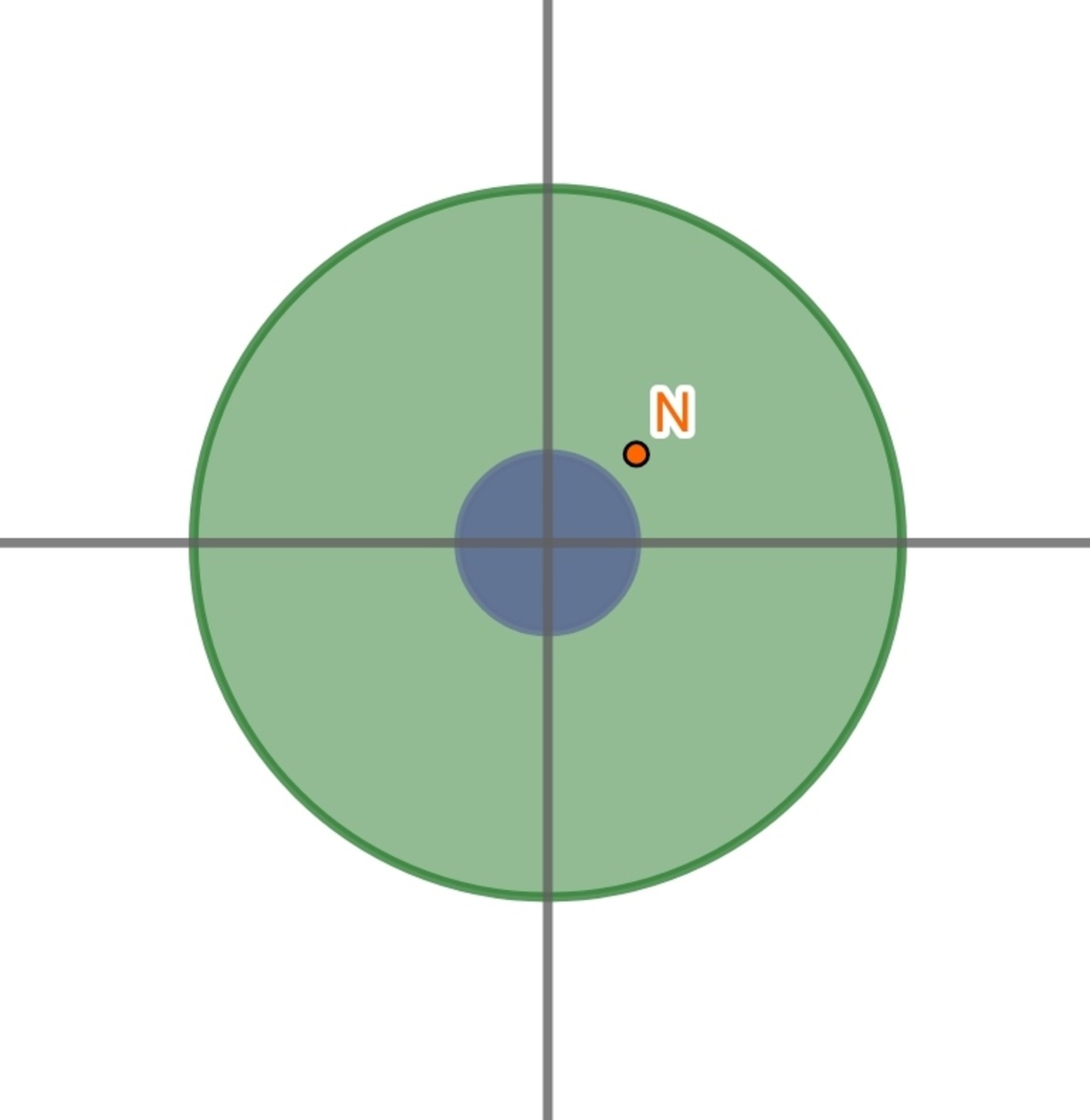
A particle with charge q = + 10 q=+10 is position at N N ( x , y , z ) = ( 1 , 1 , 1 ) (x, y, z) =(1,1,1) at that orange dot as shown in figure. A closed conical frustum consists of a bottom surface, a top surface and curved surface. (Green)Bottom surface has equation x 2 + y 2 ≤ 16 x^{2}+y^{2}≤16 centered at orgin and parallel to X − Y X-Y plane. The(Blue) top surface has equation x 2 + y 2 ≤ 1 x^{2} + y^{2} ≤1 centered at ( 0 , 0 , 4 ) (0,0,4) and parallel to X − Y X-Y plane. And the third surface is curved surface. I have provided the view of figure from + Z +Z direction. Let the flux passing through these 3 surfaces be ϕ 1 , ϕ 2 , ϕ 3 \phi_{1}, \phi_{2}, \phi_{3} . Determine the following ratio : ϕ 1 ϕ 2 ϕ 3 ϕ 1 + ϕ 2 + ϕ 3 \frac{\phi_{1}\phi_{2}\phi_{3}}{\phi_{1}+\phi_{2}+\phi_{3}} Details and Assumptions 1) Electric permittivity ϵ o = 1 \epsilon_{o}=1


The answer is 0.445.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Mar 14, 2020

Nice problem. Solution code is attached. The key here is that we only need to explicitly calculate the fluxes for the two disks. Then we can use Gauss's Law to get the flux for the curved surface. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
 
import math

N = 5000

#####################################

q = 10.0

xq = 1.0
yq = 1.0
zq = 1.0

e0 = 1.0

#####################################

k = 1.0/(4.0*math.pi*e0)

phi1 = 0.0
phi2 = 0.0

#####################################
#####################################
#####################################
#####################################

# Bottom Disk 

dr = 4.0/N
dtheta = 2.0*math.pi/N

nx = 0.0
ny = 0.0
nz = -1.0

r = 0.0

while r <= 4.0:

    theta = 0.0

    while theta <= 2.0*math.pi:

        x = r*math.cos(theta)
        y = r*math.sin(theta)
        z = 0.0

        dS = r*dr*dtheta

        Dx = x - xq
        Dy = y - yq
        Dz = z - zq

        D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

        ux = Dx/D
        uy = Dy/D
        uz = Dz/D

        E = k*q/(D**2.0)

        Ex = E * ux
        Ey = E * uy
        Ez = E * uz

        dot = Ex*nx + Ey*ny + Ez*nz

        dphi = dot * dS

        phi1 = phi1 + dphi

        theta = theta + dtheta

    r = r + dr

##################################################################
##################################################################

# Top Disk 

dr = 1.0/N
dtheta = 2.0*math.pi/N

nx = 0.0
ny = 0.0
nz = 1.0

r = 0.0

while r <= 1.0:

    theta = 0.0

    while theta <= 2.0*math.pi:

        x = r*math.cos(theta)
        y = r*math.sin(theta)
        z = 4.0

        dS = r*dr*dtheta

        Dx = x - xq
        Dy = y - yq
        Dz = z - zq

        D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

        ux = Dx/D
        uy = Dy/D
        uz = Dz/D

        E = k*q/(D**2.0)

        Ex = E * ux
        Ey = E * uy
        Ez = E * uz

        dot = Ex*nx + Ey*ny + Ez*nz

        dphi = dot * dS

        phi2 = phi2 + dphi

        theta = theta + dtheta

    r = r + dr

##################################################################
##################################################################

# Curved Surface
# Use Gauss Law

phi3 = 10.0 - phi1 - phi2

##################################################################
##################################################################

print N
print ""
print phi1
print phi2
print phi3
print ""
num = phi1 * phi2 * phi3
denom = phi1 + phi2 + phi3
print (num/denom)


#>>> 
#1000

#3.68046254839
#0.197988258618
#6.12154919299

#0.446070170861
#>>> ================================ RESTART ================================
#>>> 
#2000

#3.67901825264
#0.198158344657
#6.1228234027

#0.446371072157
#>>> ================================ RESTART ================================
#>>> 
#5000

#3.67625732908
#0.197985417747
#6.12575725317

#0.445860388935
>>>

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase Sir Ha Ha Ha Yes i agree with you i do not know how to calculate flux analytically through that curved surface. I just calculate through two disc and subtract it from 10 10 .

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

@Steven Chase in your code what does N = 5000 N=5000 mean??

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

For example, the disk has a radial dimension and an angular dimension. Each one of those is divided into 5000 5000 parts. So each surface ends up being divided into 25 25 million pieces. I always check the result for multiple different resolutions (N values), to be sure that the answer converges nicely as N N increases.

Steven Chase - 1 year, 2 months ago

Log in to reply

@Steven Chase – Today I started to learn code . Therefore I was asking . Simply you are doing integration . How much time does it take for you to run the code???

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

@A Former Brilliant Member – That's good. You'll find it very useful. This code will take anywhere from a few seconds to a minute or two to run

Steven Chase - 1 year, 2 months ago

Log in to reply

@Steven Chase – @Steven Chase is there any website or any YouTube channel where phython programming is well explained??

A Former Brilliant Member - 1 year, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...