General Magnetics (06/05/2020)
A small conducting loop of radius
a
and resistance
r
is pulled with velocity
v
perpendicular to a long straight conductor carrying a current
i
. If a constant power
P
is dissipated in the loop, find the variation of velocity of the loop as a function of
x
. Given that
x
>
>
a
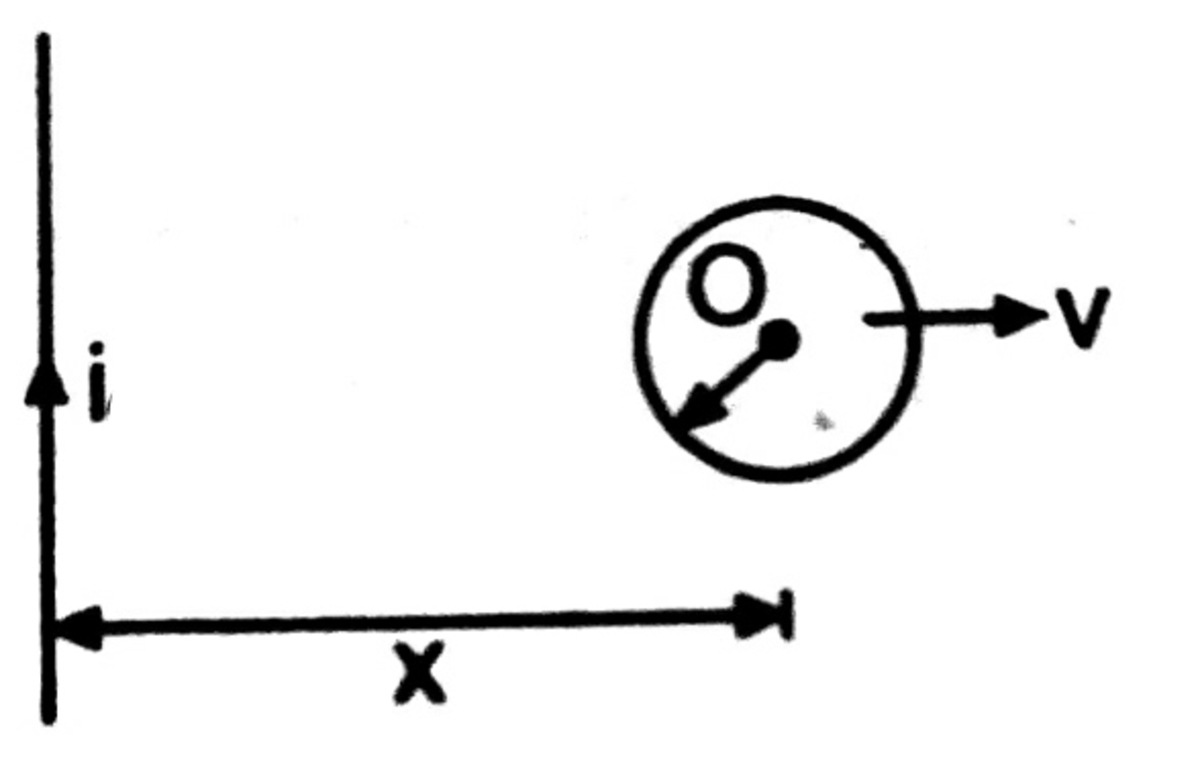
If you answer comes in the form of
μ
0
i
γ
a
δ
α
x
β
(
P
r
)
ϕ
Type your answer as
α
+
β
+
γ
+
δ
+
ϕ
=
?
The problem is not original.
The answer is 7.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath Nice solution, I just upvoted.
@Karan Chatrath
+
0
.
9
9
6
2
6
4
0
0
9
9
6
2
6
4
0
2
e
2
−
t
s
i
n
(
2
−
1
3
9
9
t
)
−
0
.
1
e
2
−
t
c
o
s
(
2
−
1
3
9
9
t
)
+
0
.
1
is it correct?? will be grateful if you reply.
Thanks in advance!
Log in to reply
No, it is not.
Log in to reply
@Karan Chatrath I have edited my equation. Is it correct now??
Log in to reply
Log in to reply
@Karan Chatrath – @Karan Chatrath I have edited my comment again. Check now!
Log in to reply
@A Former Brilliant Member – Almost correct. The coefficient of s i n should be positive. Please check your work again.
Don't worry, you made a good effort. That is appreciable.
Log in to reply
@Karan Chatrath Thanks Sir Your this comment feels me that I have corrected the question.
Magnetic flux density:
B = 2 π x μ 0 I
Flux linkage:
λ = π a 2 B = 2 x μ 0 I a 2
Induced voltage V :
V = d t d λ = d x d λ d t d x = − 2 x 2 μ 0 I a 2 x ˙
Power dissipated:
P = r V 2 = ( 2 x 2 μ 0 I a 2 ) 2 r x ˙ 2
Rearranging for x ˙ :
x ˙ = μ 0 I a 2 2 x 2 ( P r ) 1 / 2
@Steven Chase I will be happy if you follow up this
In the expression for flux linkage, it should be mentioned that x > > a , as otherwise the flux linkage will not be simply the product of magnetic induction and the area of the loop.
What numerical result do you get with that?
Log in to reply
The answer to this question is already given by Karan Chatrath .
@Steven Chase Sir I am not able to feel that magnetic vector potential A ??
What do you mean by that?
Log in to reply
@Steven Chase Sir I was just asking that what is meaning of A but I got that from wikipedia. BTW I have uploaded a new question.
Consider the circle to be a general distance x from the wire. A general chord parallel to the wire is parameterised in polar coordinates and a point of intersection of the circle and chord is:
x c = x + a cos θ y c = a sin θ
The area of a strip along the chord of thickness δ x c is:
δ A = 2 y c δ x c ⟹ δ A = − 2 a 2 sin 2 θ δ θ
The flux through this elementary strip is:
δ Φ = 2 π ( x + a cos θ ) μ o I δ A
⟹ δ Φ = − 2 π ( x + a cos θ ) 2 a 2 μ o I sin 2 θ δ θ
Considering only the magnitude, the negative sign can be dropped:
⟹ δ Φ = π a 2 μ o I ( x + a cos θ sin 2 θ δ θ )
Taking the limit as θ → 0 leads to:
d Φ = π a 2 μ o I ( x + a cos θ sin 2 θ d θ )
The magnitude of the total flux through the circle is:
Φ = π a 2 μ o I ∫ 0 π x + a cos θ sin 2 θ d θ = μ o I x … ( 1 )
Keeping in mind x > > a
Φ = π x a 2 μ o I ∫ 0 π 1 + x a cos θ sin 2 θ d θ
⟹ Φ = π x a 2 μ o I ∫ 0 π 1 + x a cos θ sin 2 θ d θ ≈ π x a 2 μ o I ∫ 0 π sin 2 θ d θ
Φ ≈ 2 x a 2 μ o I
The rest of the solution proceeds according to that of @Steven Chase . It is noteworthy that if the assumption that x > > a is not considered, then the final result is independent of x .