Generalizing floor summations

$\small{\text{Edit:In figure, ceiling function is there instead of fractional part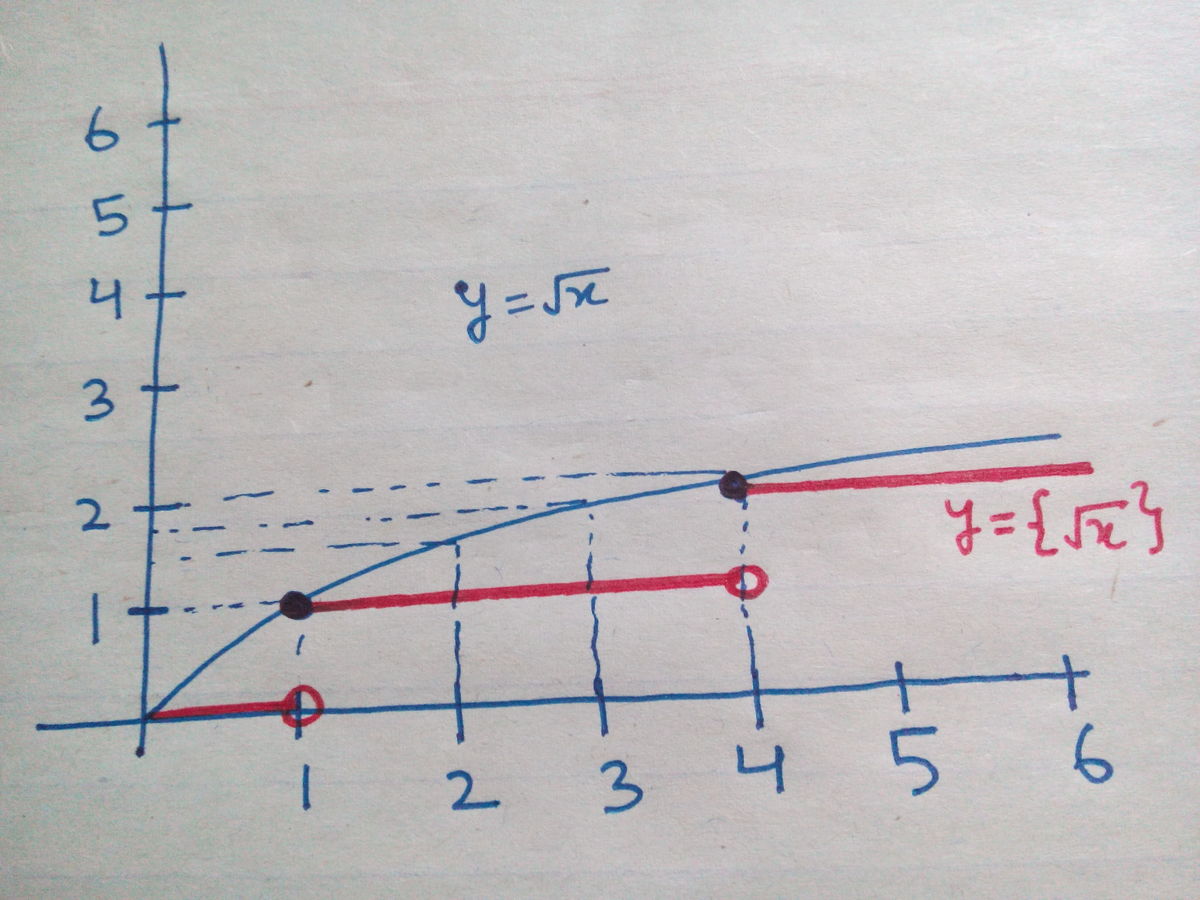}}$ $\small{\mathcal{S}=1+1+1+2+2+2+2+2+3+3\\+3+3+3+3+3+3+..}$ $=3(1)+5(2)+7(3)+9(5)+.....$ $=\displaystyle \sum_{i=1}^n (2i+1)i$ $=2 \displaystyle \sum_{i=1}^n i^2 + \displaystyle \sum_{i=1}^n i$ $=2(\dfrac{n(n+1)(2n+1)}{6})+\dfrac{n(n+1)}{2}$ $=\Large\dfrac{n(n+1)(4n+5)}{6}$

$\begin{aligned} S & = \lfloor \sqrt{1} \rfloor + \lfloor \sqrt{2} \rfloor + \lfloor \sqrt{3} \rfloor + \lfloor \sqrt{4} \rfloor + \lfloor \sqrt{5} \rfloor + \lfloor \sqrt{6} \rfloor + \lfloor \sqrt{7} \rfloor + ... + \lfloor \sqrt{(n+1)^2-1} \rfloor \\ & = \underbrace{1 + 1 + 1}_{1\times (2^2-1^2)} + \underbrace{2 + 2 + 2 + 2 + 2}_{2\times (3^2-2^2)} + \underbrace{3 + 3 + 3 + 3+3 + 3 + 3 + 3 + 3}_{3\times (4^2-3^2)} + ... n \\ & = \sum_{k=1}^n k[(k+1)^2-k^2] \\ & = \sum_{k=1}^n (2k^2+k) \\ & = 2 \sum_{k=1}^n k^2+\sum_{k=1}^n k \\ & = \frac{n(n+1)(2n+1)}{3} + \frac{n(n+1)}{2} \\ & = \frac{n(n+1)(4n+2+3)}{6} \\ & = \boxed{\dfrac{n(n+1)(4n+5)}{6}} \end{aligned}$