Generator without Prime Mover
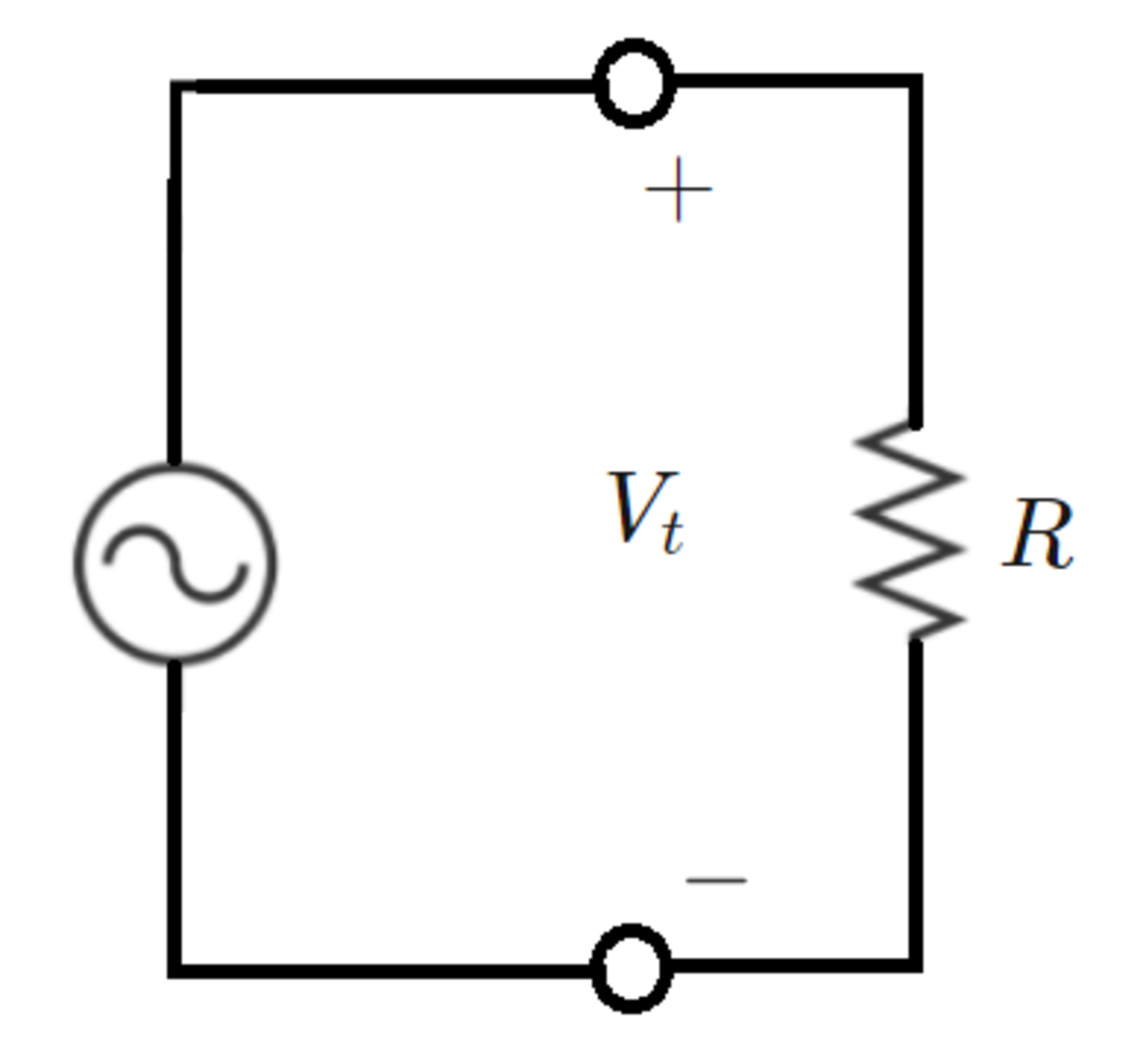
A single-phase AC electric generator has a moving rotor with a magnet, which induces a voltage V t at its stator terminals. A resistor R is connected across the stator terminals.
The machine model is as follows (neglecting prime mover - see below):
λ = ω 0 V m cos θ V t = λ ˙ d t d ( 2 1 I θ ˙ 2 ) = − P R
In the model, λ is the stator magnetic flux linkage as a function of rotor angular position θ . The terminal voltage V t is the time derivative of the flux linkage. The third equation states that the rotor is losing kinetic energy at a rate equal to the resistor power dissipation (a statement of energy conservation). The parameter I is the machine inertia constant.
At time t = 0 , θ = 0 and θ ˙ = ω 0 . Also at t = 0 , the machine loses its mechanical prime mover and begins to slow down.
At time t = 2 , what is the rotor angular speed θ ˙ ?
Bonus: Make a plot of the terminal voltage over time, and explain its characteristics
Details and Assumptions (assume standard SI units):
1)
V
m
=
1
2
0
2
2)
ω
0
=
1
2
0
π
3)
R
=
1
5
4)
I
=
0
.
0
1
The answer is 97.37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Very nice solution, thanks. There might be a follow-up to this one with the prime mover present.
Log in to reply
Thanks. Looking forward to it.
Log in to reply
It's up now
Log in to reply
@Steven Chase – @Steven Chase sir did you have done engineering in electrical. Or physics???? I want to know your graduation???
Log in to reply
@A Former Brilliant Member – I majored in electrical engineering
Log in to reply
@Steven Chase – @Steven Chase sir from which college??
Log in to reply
@A Former Brilliant Member – I went to a state university in the US
Log in to reply
@Steven Chase – @Steven Chase sir can you please upload the solution of magnetic line integral part 3 {https://brilliant.org/problems/magnetic-line-integral-part-3/}
@Steven Chase – @Steven Chase sir can you please upload the solution of magnetic line integral part 3 {https://brilliant.org/problems/magnetic-line-integral-part-3/}
Log in to reply
@A Former Brilliant Member – It's up now
Log in to reply
@Steven Chase – @Steven Chase sir Thanks. Can you please upload More questions on finding magnetic field due to ellipse. This type of questions . Please sir??
@Steven Chase sir can you please upload the solution of the problem https://brilliant.org/problems/two-magnetic-loops-part-3/
Consider the given set of equations:
V t = − ω o V m sin θ θ ˙ P R = R V t 2 = ω o 2 R V m 2 sin 2 ( θ ) θ ˙ 2
After rearrangement and simplification, the governing differential equation is:
θ ¨ = − A sin 2 ( θ ) θ ˙ A = ω o 2 I R V m 2
Now,
θ ¨ = θ ˙ d θ d θ ˙ = − A sin 2 ( θ ) θ ˙
Separating the variables, integrating and applying the initial conditions gives:
θ ˙ = − 2 A ( θ − 2 sin 2 θ ) + ω o
Now, again, Separating the variables and integrating from t = 0 to t = 2 gives:
∫ 0 θ f − 2 A ( θ − 2 sin 2 θ ) + ω o d θ = 2
Now, the angular position θ f is not known. It needs to be found by solving the above integral equation. Having found θ f its value can be replaced in the equation:
θ ˙ f = − 2 A ( θ f − 2 sin 2 θ f ) + ω o
Solving for θ f can be done iteratively. Using a Wolfram Alpha like tool, or a numerical integration scheme, one can incrementally increase the value of θ f till the integral evaluates to 2 .
The answer comes out to be: 9 7 . 3 7 6 .
As for the bonus question:
One can see that as the kinetic energy of the rotor reduces, the voltage across the terminals undergoes damped oscillations with variable frequency. This makes sense as the energy of the rotor is completely dissipated in the resistor. So naturally, the voltage across the resistor also decreases with time. This explains why the magnitude of the voltage reduces with time. I do not have one for the decreasing frequency.