Geometric Nightmare
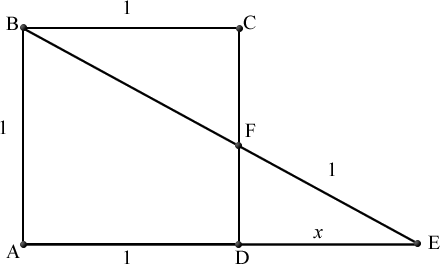 Diagram above shows a unit square
A
B
C
D
, the line
A
D
is extended to point
E
such that
B
E
is a straight line intersecting the line extended line of
A
D
at
E
with
F
as a point of
B
F
that is a point on line side
C
D
such that
F
E
=
1
. Let distance
D
E
be denoted as
x
. Find the value of
x
.
Diagram above shows a unit square
A
B
C
D
, the line
A
D
is extended to point
E
such that
B
E
is a straight line intersecting the line extended line of
A
D
at
E
with
F
as a point of
B
F
that is a point on line side
C
D
such that
F
E
=
1
. Let distance
D
E
be denoted as
x
. Find the value of
x
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This is such an elegant solution, Gabriel; no quartic polynomials to worry about. :)
Awesome ! Thanks for posting
Beautiful solution to a beautiful problem .I wonder if you or Brian or anybody else tried coordinate geometry after failing by using trigonometry.I let B(0,1) and E (P,0)giving F (1,1-1/P) . EF=1 gives a quartic in P which can be reduced to a quadratic in (P+1/P)..On solving forP ,simply subtract 1 to get x.
http://postimg.org/image/r8r03o3ch/
backward solution: x / (x+1) = sqrt( 1-x^2 ) just substitute
First note that Δ F E D and Δ F B C are similar. Thus
∣ D E ∣ ∣ D F ∣ = ∣ C B ∣ ∣ C F ∣ ⟹ x 1 − x 2 = 1 1 − 1 − x 2
⟹ 1 − x 2 = 1 + x x ⟹ 1 − x 2 = ( 1 + x ) 2 x 2
⟹ x 4 + 2 x 3 + x 2 − 2 x − 1 = 0 .
Now there is a technique for factoring quartics, but it is quite a slog so I just used WolframAlpha to confirm that the posted answer is indeed a solution to the above quartic. If anybody has a more elegant way of algebraically finding this exact value I would be most interested.
let E^=2X giving you Cotan 2X=Cos 2X+1 Solving this may give you x without having to solve the quartic
Log in to reply
How did you got this equation? Can you please elaborate!
Log in to reply
let the angle AEB= 2X then cotan 2X =cos 2X +1
That sounds interesting, but I'm not quite sure what your terms are. Is "E^" meant to indicate ∠ D E F ?
Log in to reply
yes , just not able to write it like this on my computer
Thank you sir for Link
How this equation is solve without using wolframalpha.....?
x 4 + 2 x 3 + x 2 − 2 x − 1 = 0
Well, at least we have the same quartic polynomial. :) I posted a link to a solution method in my posted answer, but it is such a mess to go through all the steps I didn't think it was worth the effort just now. I'll wait to see if anyone has a more elegant approach before tackling this 'monster'.
Log in to reply
now that we got that, we have that:
1 + 2 x = x 2 + 2 x 3 + x 4 this suggests completing the square on the lefthandside. After doing that we get: ( 1 + x ) 2 = 2 x 2 ( 1 + x + x 2 ) − x 4 then, passing the x^4 to the lhs adn dividing by x^2 (for its surely not zero) x 2 + ( 1 + x 1 ) 2 = 2 ( 1 + x + x 2 ) but we got lucky because if we substract 2 ( 1 + x ) we can complete the square in the lhs again because x ( 1 + x 1 ) = x + 1 and get ( x − 1 − x 1 ) 2 = 2 x 2 and because ( x − 1 − x 1 ) is clearly negative we get the simple quadratic equation: x − 1 − x 1 = − x 2 which is straigthforward to solve.
Log in to reply
This is really clever, Héctor; thanks for showing me the steps. Solving the last quadratic yields
x = 2 ( 1 + 2 ) 1 + 5 + 4 2 ,
which at first didn't look like the posted solution, but they are in fact equal. :)
Log in to reply
@Brian Charlesworth – Brian, thank you for your kind comment. You can get the answer proposed directly by, when you get the quadratic equation in standard form, multiplying all by 2 − 1 and so you obtain 1 as the director coefficient.
Log in to reply
@Héctor Andrés Parra Vega – Yes. It is so nice! Thanks. I did not understand your first comment .Things are clear now.
Log in to reply
@Niranjan Khanderia – Thanks to you too :)
In response to Brian Charlesworth: Two of the roots are reciprocal of one another as we see from the symmetry of coefficients. How can we use this fact ? These are the only real roots. But how do we know this?
Log in to reply
That's interesting. If α is a solution, then when I plug in x = α 1 and then multiply through by − α 4 I end up with the equation α 4 + 2 α 3 − α 2 − 2 α − 1 = 0 , which differs from the original equation in the sign for the squared term. So I don't think that in this case the two real roots are reciprocals of one another.
Log in to reply
@Brian Charlesworth
–
I am very sorry. I made mistake in writing down the equation as
x
4
−
2
x
3
+
x
2
−
2
x
+
1
.
As I do always, I used graphing calculator TI 83 Plus and graph the polynomial. I kept the window, X..[.5,.6], Y,[-1E-4, 1E-4] , scales 1E-4 after locating the point in [-10,10],[-10,10], scales 1 and knowing x<1. The answer was good to third place of decimal from the given options. One can get even better by using ENTRY key{2nd ENTER} and the given function after knowing approximately by graphing.
First, let be y = F D . As we can see, Δ F D E and Δ B A E are similar. Thus: x y = 1 + x 1 ⇒ x y = x − y .
But, from triangle F D E we can write: x 2 + y 2 = 1 .
Subtracting − 2 x y from both sides we obtain:
( x − y ) 2 = 1 − 2 x y ⇒ ( x y ) 2 = 1 − 2 x y .
Now, let's call z = x y
z 2 + 2 z − 1 = 0 .
As we know, z = x y > 0 , then z = 2 − 1 .
Thus we have 2 − 1 = x − y ⇒ y = x − 2 + 1
Substituting in the Pythagorean theorem: x 2 + ( x − ( 2 − 1 ) ) 2 = 1
2 x 2 − ( 2 2 − 2 ) x + 2 − 2 2 = 0
x 2 − ( 2 − 1 ) x + 1 − 2 = 0
x = 2 2 − 1 + 2 2 − 1