Geometric Progressions

We are given a G.P. $\{a_{n}\}$ , $a_{n} = ar^{n-1}$ , such that

$a(1 + r) = 7$ and $a(1 + r + r^{2} + r^{3} + r^{4} + r^{5}) = 91$

$\Longrightarrow a(1 + r) + ar^{2}(1 + r + r^{2} + r^{3}) = 91 \Longrightarrow a(1 + r + r^{2} + r^{3}) = \dfrac{84}{r^{2}}.$

This last equation implies that the sum of the first four terms equals $\dfrac{84}{r^{2}}.$

Now as clearly $r \ne 1,$ the second of our initial equations can be rewritten as

$a*\dfrac{(r^{6} - 1)}{r - 1} = 91,$

which when divided by the first of our initial equations yields

$\dfrac{r^{6} - 1}{(r - 1)(r + 1)} = \dfrac{91}{7} = 13$

$\Longrightarrow \dfrac{(r^{2} - 1)(r^{4} + r^{2} + 1)}{r^{2} - 1} = 13$

$\Longrightarrow r^{4} + r^{2} - 12 = 0 \Longrightarrow (r^{2} + 4)(r^{2} - 3) = 0.$

As $r$ is real we must have that $r^{2} = 3,$ and so $\dfrac{84}{r^{2}} = \boxed{28}.$

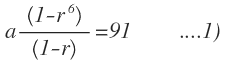
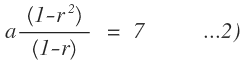
Divide Equ 1 by 2 and apply cubic identities, you will get a Quadratic Equ with

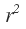
Solve it you get

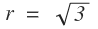
What else do we need now!!

Let say G.P; first terms $a,$ ratio $r$ and the sum of the first $n$ terms is $S_n,$

$S_n= \frac{a(r^n-1)}{r-1}$

So we have,

$S_2=\color{#3D99F6}{ \frac{a(r^2-1)}{r-1}=7} ...(1)$ $S_6= \frac{a(r^6-1)}{r-1}=91 ...(2)$

$(2):(1),$

$\dfrac{\frac{a(r^6-1)}{r-1}}{\frac{a(r^2-1)}{r-1}}=\dfrac{91}{7}$

Because $A^3-B^3=(A-B)(A^2+AB+B^2),$

$\frac{(r^2-1)(r^4+r^2+1)}{r^2-1}=r^4+r^2+1=13$

$\implies r^4+r^2-12=0\implies r^2=3$

$S_4= \frac{a(r^4-1)}{r-1}= \color{#3D99F6}{\frac{a(r^2-1)}{(r-1)}}(r^2+1)=\color{#3D99F6}{7}(3+1) =\boxed{28}$

Genesis,where did you get this one from???

Lets call the reason between the elements of n. X+xn+xn^2+xn^3+xn^4+xn^5=91 X+xn=7=x.(n+1) Xn^2+xn^3=n^2. (X+xn)=n^2. 7 Xn^4+xn^5=n^4. (X+xn)=n^4 . 7 X+xn+xn^2+xn^3+xn^4+xn^5=x+xn .(1+n^2+n^4)=91=7 . (1+n^2+n^4) Therefore(1+n^2+n^4)=13, n^2+n^4=12 n^2=3 X+xn+xn^2+xn^3=n^2 . (x+xn)+(x+xn)=3. 7 +7=28