Passel Of Techniques
A
B
C
is a right triangle with
∠
B
=
9
0
∘
.
E
and
F
are the mid-points of
A
B
and
A
C
, respectively.
The
incenter
I
of triangle
A
B
C
lies on the
circumcircle of triangle
A
E
F
,
Find the ratio A B B C .
If this ratio can be expressed as q p , where p and q are coprime positive integers, submit your answer as p + q .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I think you mean ∠ A E F = 9 0 ∘ in line (3) :) In fact, a couple statements are inconsistent with your diagram- ∠ A I F = 9 0 ∘ ...
Log in to reply
I had not seen this mistake. Thanks
Very nicely presented!
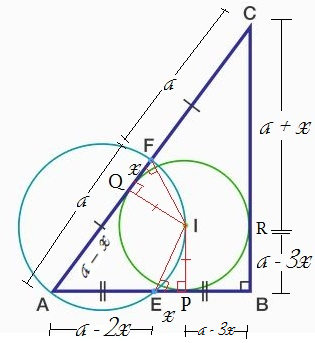
Let
B
C
=
a
,
A
C
=
b
and
A
B
=
c
.
Construction : Draw
I
D
perpendicular to
A
C
.
Then
I
D
=
r
,
the inradius of
△
A
B
C
.
Observe
E
F
is parallel to
B
C
[Mid-point theorem] and hence
∠
A
E
F
=
∠
A
B
C
=
9
0
∘
.
Hence
∠
A
I
F
=
9
0
∘
.
Therefore
I
D
2
=
F
D
×
D
A
.
If
a
>
c
,
then
F
A
>
D
A
and we have
D
A
=
s
−
a
,
and
F
D
=
F
A
−
D
A
=
2
b
−
(
s
−
a
)
.
Thus we obtain
r
2
=
4
(
b
+
c
−
a
)
(
a
−
c
)
but
r
=
2
c
+
a
−
b
.
From these two equations we get
(
c
+
a
−
b
)
2
=
(
b
+
c
−
a
)
(
a
−
c
)
.
Simplification gives
3
b
=
3
a
+
c
.
Squaring both sides and using
b
2
=
c
2
+
a
2
,
we obtain
4
c
=
3
a
.
Hence
B
A
B
C
=
c
a
=
3
4
.
Therefore, the sum of numerator and denominator
=
4
+
3
=
7
.
Note:
If
a
≤
c
,
then
I
lies outside the circumcircle of
△
A
E
F
.
your method is great and simple
i solved this by pure trigonometry
r= 2R*sin^2(A/2)
this what i got at the end
and then
2a = b+c
and then a/c =4/3
Hey Ayush! I've read ur profile & it's worthy of praise.Really we all are learning &sharing ideas.
Log in to reply
what made u to tell me that iam worthy of praise?
Log in to reply
Ur respect 2ward the subject & it seems u realise the vastness & range of any subject which we can only be amazed at.
Log in to reply
@Kaushik Chandra – I agree with you terry , he is worthy of praise
Log in to reply
@A Former Brilliant Member – thanks a lot !
@A Former Brilliant Member – Thanx a lot Neel for supporting my view.
Log in to reply
@Kaushik Chandra – Hey Neel why don't u write a solution of ur own for this question. We will enjoy the application trigonometry in this marvellous question. NOTE : It's just an advice u may follow it or not.
Log in to reply
@Kaushik Chandra – of course , why not
i will do that
Log in to reply
@A Former Brilliant Member – Thanks a lot Neel for supporting my advice. It means a lot to me.
Log in to reply
@Kaushik Chandra – Neel ur profile is just amazing. Very beautiful. And , Thanks a lot for following me.
Log in to reply
@Kaushik Chandra – you are welcome
@Kaushik Chandra – Hey terry are you on slack ? I would love to talk to you If not Go here https://brilliant.org/slackin/
Log in to reply
@A Former Brilliant Member – Of course Neel, I would also enjoy ur company. And I am not on slack right now but will join very soon. CHEERS!
Log in to reply
@Kaushik Chandra – when are u going to join
@Kaushik Chandra – Thanks to both of u for the praise.
@Kaushik Chandra – thanks a lot!
Nice solution . It so happens that the line joining the centre of the larger circle and the incentre of the smaller circle is parallel to the line BC. But is there a way of proving that this must be so because from such a proof the solution to the problem follows pretty quickly
Log in to reply
I think u meant || to AB. I think so. They maybe or since it is a right triangle this thing satisfies.
This question appeared in gmo last year and this is the exact same official solution which they gave.
Log in to reply
Well I had written GMO and this was the same solution i wrote.

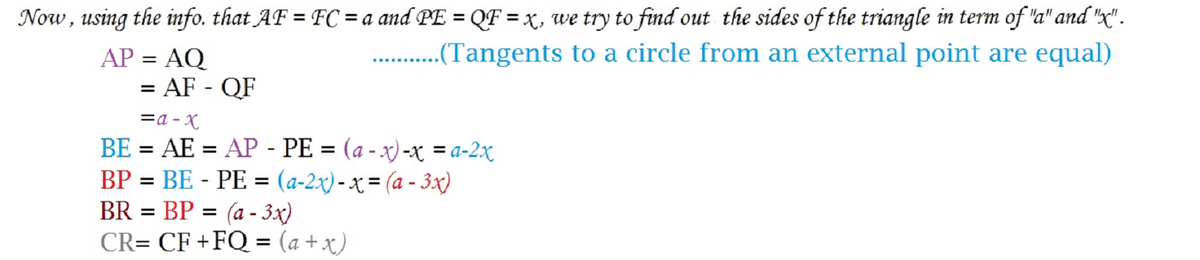


 Note:If
a
≤
x
,
then I lies outside the circumcircle of
△
A
E
F
.
Note:If
a
≤
x
,
then I lies outside the circumcircle of
△
A
E
F
.
Are you himanshu
Log in to reply
Now what problem why doesn't it appears as it need to be
If you want a i − 1
If you 2^3
KUDOS! Neel for ur beautiful solution. It was cool & of course Mathematics needs a lot of attention (as ur profile also says).
Log in to reply
Hi terry thank you for your kind words
Why don't u join slack
We can talk there
U did this for an unknown guy like me .It's praiseworthy Neel,really very praiseworthy.
(1) As A I is a bisector then, we can say that ∠ F A I = ∠ I A E = α .
(2) Now, A E I F is a ciclic quadrilateral ⟹ ∠ I E F = I F E = α and Δ I F E is isosceles.
(3) F and E are midpoints then F E ∥ B C and ∠ A E F = 9 0 ∘ implies ∠ A F E = 9 0 ∘ − 2 α implies ∠ A I F = 9 0 ∘ − α ⟹ ∠ I F C = 9 0 ∘ + α .
(4) As H is a intersection of the bisector A I and Δ A B H is a triangle rectangle then ∠ A H B = 9 0 ∘ − α ⟹ ∠ A H C = 9 0 ∘ + α .
(5) As C I is a bisector of ∠ A C B = 9 0 − 2 α then ∠ A I C = ∠ I C B = 4 5 ∘ − α and as ∠ A H C = 9 0 ∘ + α = ∠ I F C an share C I ⟹ Δ F I C ⪰ Δ I C H then ∠ F I C = ∠ I H C = 4 5 ∘ .
(6) As Δ F I C ⪰ Δ I C B then I F = I H = I E then H , F , E are cyclic then ∠ F I H is central and ∠ F E H = 4 5 º ⟹ ∠ H E B = B H E = 4 5 ∘ then Δ H E B is isoceles and E B = B H .
(7) E B = B H . and for (5) C F = C H then if E B = x and C H = y we have that
4 y 2 − 4 x 2 = x 2 + y 2 + 2 x y ⟹ 5 x 2 + 2 x y − 3 y 2 = 0 = ( 5 x − 3 y ) ( x + y ) but x + y are not 0 then 5 x − 3 y = 0 ⟹ 5 x = 3 y .
Now, A B B C = 2 x x + y = 2 1 + 2 x y = 2 1 + 6 5 = 1 2 1 6 = 3 4 then p + q = 4 + 3 = 7