Not as They Seem to Be
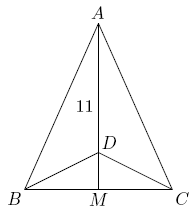 Triangle
A
B
C
is isosceles, with
A
B
=
A
C
and altitude
A
M
=
1
1
.
Suppose that there is a point
D
on
A
M
with
A
D
=
1
0
and
∠
B
D
C
=
3
∠
B
A
C
.
Then the perimeter of
△
A
B
C
may be written in the form
a
+
b
,
where
a
and
b
are integers. Find
a
+
b
.
Triangle
A
B
C
is isosceles, with
A
B
=
A
C
and altitude
A
M
=
1
1
.
Suppose that there is a point
D
on
A
M
with
A
D
=
1
0
and
∠
B
D
C
=
3
∠
B
A
C
.
Then the perimeter of
△
A
B
C
may be written in the form
a
+
b
,
where
a
and
b
are integers. Find
a
+
b
.
The answer is 616.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Took me more time to figure out that 1 1 5 = 6 0 5 than solving the problem.
@Parth Lohomi Please do not set all of your problems as level 5. If this continues, I might be forced to make you unable to set problems at level 5.
Log in to reply
Which level it should be?
Log in to reply
Ideally, set it based on the level of other problems that you have seen / solved. That will allow us to release the ratings earlier, instead of seeing huge changes from when we release them, to when they actually settle down.
If everyone sets a reasonable level, then we can speed up the process. If several people insist on setting the wrong level, then I will be forced to delay the process, in order to achieve more consistency.
As an example, asking a question of "What is sin 1 5 ∘ ?" should not be in level 5. It should settle down around level 2-3 (depending on how the problem is phrased / answers are given), as it is a relatively simple application of the double angle formula.
sorry sir!
sir can i know who sets the level of problems
I had the same solution, except that I used the identity tan 3 x = 1 − 3 tan 2 x 3 tan x − tan 3 x
Log in to reply
Nice choice. It was just that this old man don't remember the formula.
Log in to reply
If 57 is so old, what is 87? More than two legs in grave?
Log in to reply
@Niranjan Khanderia – Sorry, sir, I have to watch out my words.
Log in to reply
@Chew-Seong Cheong – No. I only want to tell you that YOU ARE NOT Old . 87 is really quite old. A leg in the grave. I have no problem with that. Good luck.
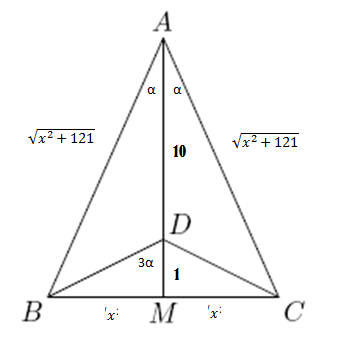
∠ B A M = α , ∠ B D M = 3 α and B M = x
tan α = 1 1 x and tan 3 α = x so tan 3 α = 1 1 tan α .
Now
tan 3 α = cos α cos 2 α − sin α sin 2 α sin α cos 2 α + sin 2 α cos α
tan 3 α = cos α ( cos 2 α − 2 sin 2 α ) sin α ( cos 2 α + 2 cos 2 α )
We get that
cos α ( cos 2 α − 2 sin 2 α ) sin α ( cos 2 α + 2 cos 2 α ) = 1 1 tan α
cos 2 α − 2 sin 2 α cos 2 α + 2 cos 2 α = 1 1
Smplifying
cos 2 α = 4 0 3 2 = 0 . 8 but cos 2 α = ( x 2 + 1 2 1 1 1 ) 2 = x 2 + 1 2 1 1 2 1
x 2 + 1 2 1 1 2 1 = 0 . 8 ⇒ x = 5 . 5
△ A B C perimeter is 2 x + 2 x 2 + 1 2 1
Perimeter is 1 1 + 2 ( 5 . 5 ) 2 + 1 2 1 = 1 1 + 2 4 6 0 5 = 1 1 + 6 0 5
Finally, a + b = 1 1 + 6 0 5 = 6 1 6
You may use /large so that we get bigger figures !
My approach was similar but using the Archimedes method for trisection.
calling BD=R we get Rcos(3x)= 1 and 2Rcos(x)=10
Then cos(x)=5cos(3x).
From that point the nitty gritty and hateful trigonometry manipulation. As said for somebody it had been kinder express the result as 11(1+sqrt(5))
I too agree, 1 1 ( 1 + 5 ) is better.
Let ∠ B A M = θ and B M = a . Therefore, ∠ B D M = 3 θ
⇒ tan θ = 1 1 a and tan 3 θ = a ⇒ tan 3 θ = 1 1 tan θ
Let t = tan θ then we have:
tan 3 θ = 1 1 tan θ ⇒ 1 − t ( 1 − t 2 2 t ) t + 1 − t 2 2 t = 1 1 t ⇒ 1 − t ( 1 − t 2 2 t ) 1 + 1 − t 2 2 = 1 1
⇒ 1 − t 2 − 2 t 2 1 − t 2 + 2 = 1 1 ⇒ 1 − 3 t 2 3 − t 2 = 1 1 ⇒ 3 − t 2 = 1 1 − 3 3 t 2
⇒ 3 2 t 2 = 8 ⇒ t = 2 1
⇒ a = 2 1 1 ⇒ A B = 2 1 1 5
Therefore, the perimeter is 1 1 + 1 1 5 = 1 1 + 6 0 5
⇒ a + b = 1 1 + 6 0 5 = 6 1 6