M2S3: From 11 to 25
In the game of M2S3, the goal is to use minimum number of steps to get from one number to the next. In each step, you can either
- multiply by 2, or
- subtract 3.
For example, if we wanted to get from 8 to 11, we could do so in 5 steps:
8 ⟶ − 3 5 ⟶ × 2 1 0 ⟶ − 3 7 ⟶ × 2 1 4 ⟶ − 3 1 1 .
What is the minimum possible number of steps required to get from 11 to 25?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Moderator note:
Great explanation of how to work backwards. Compared to the working forward approach, this greatly reduces the number of cases we have to look at. For a visual representation, see Kevin Chung's solution.
Common mistakes:
-
An approach claims that when working backwards, we should always divide by 2 each time we get an even number, and add 3 each time the number is odd. Though this claim is true when going from 11 to 25, can you find a counter example?
-
An approach that considers the number of × 2 that we need, and then minimizes the number of − 3 that we need. However, this the naive optimization doesn't necessarily yield the actual minimum. Though this claim is true when going from 11 to 25, can you find a counter example?
Working backwards is a smart strategy! Unlike the straightforward method where each number branches out two cases, this method has fewer cases to consider.
In response to Challenge Master note:
One
The easiest counterexample would be going from 3 1 to 2 5 , which can be done in two steps: 2 5 ← 2 8 ← 3 1 . If we would mindlessly divide by two for each even number, we would miss this solution.
Two
The "naive" approach assumes that the minimal solution must have the smallest possible number of multiplications with two. But it might be that adding a few doubling operations removes the need for even more subtractions.
I have not found a counterexample. In fact, the computer tells me that for x , y < 2 0 0 0 0 , the "naive" solution to find a path x → y is actually the minimal path...
Log in to reply
For 2, I was concerned about "But it might be that adding a few doubling operations removes the need for even more subtractions."
After digging further into the theory, I now start to believe that the naive approach does indeed yield the best solution. Let me lay it out:
Suppose we want to go from a to b where we multiply by 2 n times. We must have 2 n a > b and 3 ∣ 2 n a − b .
Consider the binary base representation of these numbers.
Let
a
=
a
x
a
x
−
1
…
a
0
2
.
Let
b
=
b
y
b
y
−
1
…
b
0
2
.
Let
c
=
3
2
n
a
−
b
=
c
z
c
z
−
1
…
c
1
2
.
Claim: (possibly slightly off in the indexing) Given exactly
n
multiplications, the minimium number of steps is equal to:
M
S
(
a
,
b
,
n
)
=
n
+
(
number of 1’s in
c
i
for
i
=
1
0
to
n
−
1
)
+
c
z
c
z
−
1
…
c
n
2
(interpreted as a decimal)
Other than the n multiplications, the latter terms account for how best to subtract 3 optimally - If you subtract twice, just push it before a multiplication, until there is no more multiplication signs, in which case you have to subtract all of them.
Claim: (not fully certain) Over all
n
,
M
S
(
a
,
b
,
n
)
is minimial when
n
is minimal. IE The naive solution is the best.
(This part is tricky because
c
changes.)
Log in to reply
You may want to edit your comment to make the last part legible.
My investigation last night went along similar lines as yours. I have no watertight proof, but come very close-- and the computational evidence is strong too.
Yesterday I ended up writing S ( x , y , n ) = n + q + # 2 r , p = 3 2 n x − y = 2 n q + r , r < 2 n with precisely the same meaning as your formula for M S ( a , b , n ) .
Here are my further thoughts. I focus on the case 3 ∣ x , y , in which n must be even iff x ≡ y and odd iff x ≡ y mod 3.
Increasing n by two results in p ′ = 2 n x + p , which leaves the existing digits of r unchanged, but adds digits in the front. The value of q does not decrease, since q = ⌊ p / 2 n ⌋ = ⌊ 3 1 ( x − y / 2 n ) ⌋ is an increasing function of n .
Log in to reply
@Arjen Vreugdenhil – I observed a similar pattern too. If only one of a , b is divisible by 3 , then it is impossible to reach b from a .
If both a and b are divisible by n , then the problem becomes equivalent to multiply by 2, subtract 1. ( × 2 , − 1 ) . I believe a similar algorithm can be followed for this case.
For the remaining cases where a , b are both not divisible by 3 :
We want to show that M S ( a , b , n ) is minimal when n is minimal. The sequence of numbers is bounded above by 2 b . As we increase n , we are increasing the multiplications occurring in the sequence, and since the sequence cannot cross 2 b , cycles are formed.
M S ( 1 1 , 2 5 , 3 ) = 7 . The sequence is 1 1 → 8 → 5 → 1 0 → 7 → 1 4 → 2 8 → 2 5 .
M S ( 1 1 , 2 5 , 5 ) = 1 1 . The sequence is 1 1 → 8 → 5 → 2 → 4 → 8 → 5 → 1 0 → 7 → 1 4 → 2 8 → 2 5 . The 5 → 2 → 4 → 8 → 5 cycle is unnecessary.
As a result, M S ( a , b , n ) increases as n increases. These cycles are redundant, and can be eliminated by choosing a smaller n . Hence to minimize M S ( a , b , n ) , we should minimize n .
Log in to reply
@Pranshu Gaba – Pranshu, I appreciate your contribution pointing out the cycles. However, I am not yet convinced why increasing the number of multiplications n should necessarily generate cycles.
My algorithm to generate a sequence is as follows (for the case 3 ÷ x , y ): First, let n be the smallest positive integer such that 2 n x > y and n is even if x ≡ y or n is odd if x ≡ − y mod 1. Then calculate p = 3 2 n x − y , and split p = 2 n q + r with r < 2 n . The sequence is now generated as follows: first, execute the subtraction " − 3 " q times. Then multiply " × 2 " n times; after the ( n − k ) -th multiplication perform a subtraction " − 3 " iff the k -th bit of r equals 1. I summarize this sequence by writing q ∣ r with r in its binary representation. For the examples you give we have M S ( 1 1 , 2 5 , 3 ) : p = 3 8 ⋅ 1 1 − 2 5 = 2 1 = 8 ⋅ 2 + 5 ; ⟹ 2 ∣ 1 0 1 ; M S ( 1 1 , 2 5 , 5 ) : p = 3 3 2 ⋅ 1 1 − 2 5 = 1 0 9 = 3 2 ⋅ 3 + 1 3 ; ⟹ 3 ∣ 0 1 1 0 1 ; and we easily add M S ( 1 1 , 2 5 , 7 ) : p = 3 1 2 8 ⋅ 1 1 − 2 5 = 4 6 1 = 1 2 8 ⋅ 3 + 7 7 ; ⟹ 3 ∣ 1 0 0 1 1 0 1 .
Your claim seems to be that the sequence 2 ∣ … (two subtractions starting at 11) has the same effect as the sequences 3 ∣ 0 1 … , and 3 ∣ … has the same effect as 3 ∣ 1 0 … . This is easy to check: 1 1 → 8 → 5 vs. 1 1 → 8 → 5 → 2 → 4 → 8 → 5 , and 1 1 → 8 → 5 → 2 vs. 1 1 → 8 → 5 → 2 → 4 → 1 → 2 , but I would like to see proof that this kind of cycling will always happen. In a way my observation that with increasing n , r only adds binary digits up front without changing the existing digits claims the same thing, but a more intuitive proof of cyclic behavior would be nice.
Log in to reply
@Arjen Vreugdenhil – It is in fact not necessary that increasing the number of multiplications should generate cycles. If a is large, then there would be no cycles initially, and it would take more number of multiplications before cycles start to generate. I just wanted to show a rough idea of why the number of steps increases as the number of multiplications increases.
Your algorithm very elegantly shows why MS(a, b, n) is a non-decreasing sequence with respect to n , and therefore number of steps required strictly increases as n increases.
Since we are having so much fun, I put together a Wiki page about this here . Feel free to add/edit/etc.!
From what I can see, the only way in which 2 might not yield an optimal solution is if we have a negative target. For instance, to go from 1 to -20 doesn't require any × 2 s: 1 ⟶ − 3 − 2 ⟶ − 3 − 5 ⟶ − 3 − 8 ⟶ − 3 − 1 1 ⟶ − 3 − 1 4 ⟶ − 3 − 1 7 ⟶ − 3 − 2 0 But it's obviously better to do this: 1 ⟶ − 3 − 2 ⟶ − 3 − 5 ⟶ × 2 − 1 0 ⟶ × 2 − 2 0
I’m not as advanced as most of you, but what I did is work out that 25 isn’t a multiple of 2, so the only way of getting to 25 is -3, which then meant the previous number was 28. 28 is a multiple of 7, which can be reached by x2 7 twice. 11 - (2x3) = 11-6=5. 5x2=10. 10-3= 7. 7x2= 14 x2= 28. 28-3= 25. You count your steps, and there are 7 steps. I hope this way of explaining helps younger users understand the problem 😬
If we tried to work forwards, then each time we have 2 possible paths to go, and after n steps there are 2 n possibilities to track. Instead, if we work backwards, we can eliminate some paths - If we had an odd number then we could only have "subtract 3" to get there, instead of "multiply by 2".
We display the steps in the following table. If the number is odd, then we just add 3 and display it directly below. If the number is even, then we split off where the left branch divides by 2, and the right branch adds 3.
We see that the first 11 appears in the 7th previous step. Hence, the answer is 7.
Great work!
Beautiful diagram! It shows all the possibilities after n steps from the end very clearly.
Very Professional diagram! And its easy to read!
The sequence of operations is: − 3 , − 3 , × 2 , − 3 , × 2 , × 2 , − 3 .
To arrive at it, we can start by determining the minimum number of multiplications by 2. A single one will not get us high enough. Two will result in a number which will have a remainder of 2 after division by 3. We need 25, which has a remainder of only 1. Subtracting 3's before or after multiplication by 2 will not change the value of the remainder, so multiplying twice will not work. So the minimum number of multiplications by 2 is 3.
To minimize the number of subtractions, we want to do them before multiplication whenever possible. (We would have to subtract 3 twice instead of once if it is done later.) Subtracting 3 from 11 twice gets us down to 5. (Any lower and multiplying by 2 three times ends in too small a number.) We multiply once, to get 10, and see if we can subtract a 3 and still get above 25 after multiplying by 4. We can do that once, and get 7. 7 times 4 is 28. Subtract 3 and we are done.
Moderator note:
This solution claims that: The minimum number of steps from
a
to
b
is given by:
1. Fiind the minimum
n
such that
2
n
a
>
b
and
2
n
a
≡
b
(
m
o
d
3
)
.
2. Now, going from
2
n
a
to
b
, we minimize the number of "subtract 3" that is needed (see Pranshu's binary counting).
Can you spot the logical error(s) made? Can you find a counter example where this algorithm doesn't yield the minimum number of steps?
There is some observation to eliminate invalid solution, but it is still not clear to me what is the promising way to solve this problem. Do you know what step you should take next? Or there are still some trial and errors?
Reading your solution for the first time, this line could use some explanation for why we are dividing by 3. There is no division by 3 mentioned in the original problem. "Two will result in a number which will have a remainder of 2 after division by 3."
The solutions given was not meant to be a general solution applicable to all such problems, only a rational way of arriving at an answer to this particular problem. So counter-examples are likely to exist.
Log in to reply
In the discussion on Arjen's solution, even though there is a logical gap, it seems like there are no counter-examples. This provides support that the gap could be patched (by tracking through all of the details).
Your solution are equivalent to mine. ☺️
As already pointed out, you need to show that the number of "Multiply by 2" steps should be 3. (I suggest breaking this down into three questions:
Why not 7 or more?
Why not 4 or 6?
Why not 5?
Those are each dealt with easily, but shouldn't be omitted.)
But that aside, I think it's helpful to note that just doing those three steps would result in 88, i.e. an excess of 88-25=63=3*21=3(8+8+4+1). That gives a pretty good idea of how to minimize the number of "Subtract 3" steps. (And yes, the choice to write 8+8 rather than 16 is deliberate.)
Log in to reply
As already pointed out, you need to show that the number of "Multiply by 2" steps should be 3. (I suggest breaking this down into three questions:
Why not 7 or more?
Why not 4 or 6?
Why not 5?
Those are each dealt with easily, but shouldn't be omitted.)
Alternately, though, you could deal with all of those at once, in the form: Can we get the desired result, 25, by doing (in any order) 4 or more "Multiply by 2" steps and 2 or fewer "Subtract 3" steps?
No we cannot, because the smallest possible result of those steps would be ( 1 1 − 3 − 3 ) ∗ 2 ∗ 2 ∗ 2 ∗ 2 = 8 0 .
As a first attempt, we keep doubling until we reach a number that is greater than 25 and congruent to 25 modulo 3. Obviously, we can then reach 25 without any further doubles - just keep subtracting 3. The challenge is to find the optimum points at which to subtract 3.
In this case, we double 3 times, to 88. We have to subtract 63. Subtracting 3 after doubling thrice is just subtracting 3 from the final result. Subtracting 3 after doubling twice is equivalent to subtracting 6 from the final result. Subtracting 3 after doubling once is equivalent to subtracting 12 from the final result. Subtracting 3 before any doubling is equivalent to subtracting 24 from the final result.
63 = 24 + 24 + 12 + 3 gives us the minimum number of subtractions, a total of 7 steps.
If we tried doubling more times, we would have to subtract 151, 327, etc. In each case, we would only have to subtract more 24s, therefore this cannot possibly lower the total number of steps.
Moderator note:
This solution claims that: The minimum number of steps from
a
to
b
is given by:
1. Fiind the minimum
n
such that
2
n
a
>
b
and
2
n
a
≡
b
(
m
o
d
3
)
.
2. Now, going from
2
n
a
to
b
, we minimize the number of "subtract 3" that is needed (see Pranshu's binary counting).
Can you spot the logical error(s) made? Can you find a counter example where this algorithm doesn't yield the minimum number of steps?
I got lost in the part "subtracting 3 after doubling thrice is just subtracting 3..." can you clarify?
Log in to reply
Subtracting 3, 6, etc. from the final result. I've added this phrase for clarification.
Log in to reply
I understand it now, thanks for the clarification!
Good solution!
I'd like to add an explanation on why the first part works. Let's say the difference is x . Subtracting 3 from x doesn't affect the remainder of x when divided by 3 . Hence, we must multiply x by 2 until it is greater than the target number and is divisible by 3.
Great solution! I loved how you systematically found out the optimum number of steps. It is more efficient to subtract as soon as possible, but we don't want to subtract too much that we go below 25.
By writing 63 as sum of 24, 12, 6, and 3, it becomes clear what is the maximum number of times we can subtract 24. In other words, we want to find a , b , c , d such that a × 2 3 + b × 2 2 + c × 2 + d × 2 0 = 3 8 8 − 2 5 and a + b + c + d is minimized.
We see that 2 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 2 1 , so the minimum number of subtractions is 2 + 1 + 1 = 4 and we doubled 3 times, so a total of 7 steps.
Log in to reply
I like how you used the binary number to help calculate the minimum number of steps.
However, I would like to point out that your approach makes an assumption about certain values. Can you spot that assumption?
Hint: Where does Pranshu's counting break down? For example, if we only multiplied by 4, how many steps do we need to use to subtract 63?
Log in to reply
If we tried doubling more times, we would have to subtract 151, 327, etc. In each case, we would only have to subtract more 24s, therefore this cannot possibly lower the total number of steps.
I think the error is in this statement. If we doubled more times, then we are allowed to subtract higher powers of 2 like 48, 96, etc. We cannot directly say that doubling more times will result in more steps.
If we only multiplied by 4, then we can't subtract 24. 6 3 = 3 ( 5 × 2 2 + 0 × 2 1 + 1 × 2 0 , so we would need 5 + 0 + 1= 6 steps to subtract 63.
With respect to the CM note:
Hint: In order to minimize f ( x ) + g ( x ) we cannot simply find the value of c that minimizes f ( x ) , and then calculate f ( c ) + g ( c ) .
Hint: Where does Pranshu's counting break down? For example, if we only multiplied by 4, how many steps do we need to use to subtract 63?
Given that there are two operations, this immediately jumped out to me as a binary tree problem (I have no idea if that's the correct name, or if that name refers to something completely different but it's the only thing I can think to call problems like this). By that I just mean a problem than can be drawn out using a binary tree like structure. The root of the tree being 11 in this case, and each child node being the result of one of the two possible operations. Then, let each branch extend until either it has a value greater than or equal to 28 or less than or equal to 0 (since 28 would allow 1 additional step to get to 25, where larger values would require reduction before being useful which just adds extra steps. It is impossible to reach a value greater than 0 once it is reached given these operations), or it is the target value. Then compute the shortest path from the root to a target node and that's the number of steps. This particular problem is actually simple enough you could write it out by hand using this method. Idk if this image is going to show (and go easy I made it in paint), but you'll see I used arrows to indicate loops instead of just writing the whole tree again. Also one shady use of an asterisk that I hope should still be obvious what I mean.
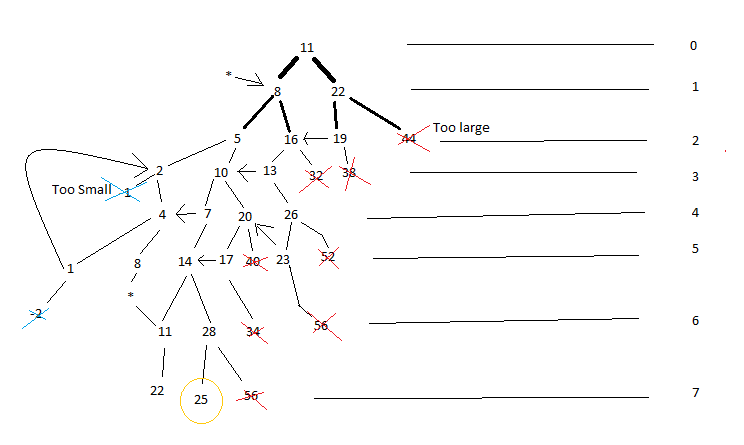
Fwiw, i think you can also stop every time you reach a number that was already part of the tree (like 8 and 11), since any path through the current node will correspond to a shorter path through the earlier appearance.
PS Nice observation to remove any value above 28, since repeated subtractions of 3 can be accomplished quicker by subtracting before multiplying by 2.
11-3=8 8-3=5 5x2=10 10-3=7 7x2=14 14x2=28 28-3=25
Well, what I did was make a node-edge graph with edges being arrows and wrote down possible combinations. Not the most efficient way I guess but managed to get the answer with it.
11-3=8 8-3=5 5x2=10 10-3=7 7x2=14 14x2=28 28-3=25
Solution -3,-3,×2,-3,×2,×2,-3
11, 8, 5, 10, 20, 40, 80, 160.
So my approach was much less insightful and naive than almost everyone here, but I spent a good amount of time on it and I was proud of myself enough to share it here. I basically wrote up some python code (copied below) that would take a start point (i) and an end point (o), and randomly either multiplied by 2 or subtracted by 3. It would save that list of operations, until our 'counter' (which started at 11) either goes above 2x25 or below 0. If that happens then the counter would go back to 11 and our list, p, is emptied (basically start all over again). After running several runs of this method for "path(11,25)" I found that 7 was the smallest length of "p" that I got, which I'm sure has some statistical significance too of being the shortest path.
In a nutshell, it's a computer doing random (but bounded) trial and error to find different paths from 11 to 25, the shortest of which over several runs was 7, which gave me enough confidence to believe that the shortest route is 7 steps. [s,s,m,s,m,m,s].
This problem actually got me to sign up for Brilliant, I'm really looking forward to what you all think, and the insight (if any) to be provided on this method. I'll be checking some of the courses too, really excited to be learning properly again!
import random
def path(i,o): #i=start, o=end
c = i #c is the counter
p = [] #p is our path
operations = ['s','m'] #s for subtract and m for multiply
while c>0:
rand_op = random.choice(operations)
if rand_op=='s':
c=c-3
p.append('s')
else:
c=c*2
p.append('m')
if c>2*o or c<0:
c=i
p=[]
print(c)
if c==o:
break
print(p)
print('End')
Working forwards, we can see that the output in mod 3 is only affected by the x2 function, not the -3 function. Thus, the quantity [11x 2^y (mod 3)] would have to be congruent to [25 (mod 3)], given that y is the number of times that x2 is used.
However, since we can only make the actual quantity smaller with the -3 function, the quantity [11x 2^y (mod 3)] would have to be greater than 25. And, because we want to minimize the number of steps it takes to the final output, we want to find the smallest quantity that fits these criteria) We find that the smallest possible quantity that fits these criteria to be 88 (as 11 and 22 are both too small, and 44 is not congruent with 25 in mod 3). Thus, y = 3.
Playing around with 88 a bit:
8( 11 ) - 25 = 63
8( 11 ) - 63 = 25
8( 11 ) + 21( -3 ) = 25
Thus, 21 effective uses of -3 are needed to bring 88 to 25.
Working backward from there:
8( 11 ) + 21( -3 ) = 25
8( 11 ) + 20( -3 ) -3 = 25
{4( 11 ) + 10( -3 )} x2 -3 = 25
{2( 11 ) + 5( -3 )} x2 x2 -3 = 25
{2( 11 ) + 4( -3 ) -3 } x2 x2 -3 = 25
{[( 11 ) + 2( -3 )] x2 -3 } x2 x2 -3 = 25
{[ 11 -3 -3 ] x2 -3 } x2 x2 -3 = 25
Therefore, we can get from 11 to 25 in 7 steps
The " × 2 " step "toggles" the number's congruence m o d 3 from either 1 to 2 or vice versa while the "subtract 3" step retains the number's congruence m o d 3 . 1 1 ≡ 2 m o d 3 2 5 ≡ 1 m o d 3 Since the numbers satisfy the congruences above, the " × 2 " step must be done on 1 1 an odd number of times. Clearly, " × 2 " should be executed at least 3 times.
If we immediately perform the " × 2 " step three times, the resulting number will be 1 1 × 2 × 2 × 2 = 8 8
This requires a reduction of 6 3 , so the " − 3 " step will need to be repeated a total of 2 1 times.
[A] If a " − 3 " step was done after the last " × 2 " step, the resulting number be will smaller by − 3 .
This equivalent to repeating the " − 3 " step once.
[B] If a " − 3 " step was done before the third (and last) " × 2 " step but after the second, the resulting number be will smaller by ( − 3 ) × 2 = − 6 .
This equivalent to repeating the " − 3 " step twice.
[C] If a " − 3 " step was done before the second " × 2 " step but after the first, the resulting number be will smaller by ( − 3 ) × 2 × 2 = − 1 2 .
This equivalent to repeating the " − 3 " step 4 times.
[D] If a " − 3 " step was done before the first" × 2 " step, the resulting number be will smaller by ( − 3 ) × 2 × 2 × 2 = − 2 4 .
This equivalent to repeating the " − 3 " step 8 times.
The " − 3 " step requires 2 1 repetitions, and these can be done in four steps by carrying out [D] twice, [C] once, then [A] once. Thus. the total number of steps required is 3 + 4 = 7 .
Since 25 cannot be obtained by multiplying with 2 hence we need to get 28 so that we can subtract 3. Now in the given example we have been given the fastest way to obtain 14 (which is 28/2) from 8 (which is 11-3) BHAM!!! solution obtained... 4 (from example) + 1(for 11-3) + 2 (to get 25 from 14 which is x2 followed by -3)
You have made some interesting observations. Can you explain why there are no other shorter ways to reach 28?
Just work backwards, and divide by two every time you get an even number, and add 3 every time an odd number appears since you cannot get an even number from multiplying by two and cannot get an odd number by subtracting 3 from an odd.
This algorithm worked in this problem, but it doesn't always work. Why should we divide by 2 every time we get an even number?
When we work backwards, we can perform either division by 2 or add 3. When we get a odd number, we have to add 3 since the sequence has only integers. However, when we have an even number, we can choose between either choice.
Consider the case where we want to reach 25 from 31.
We start with 25. We have to add 3, we get 28. Now if we want to reach 31, it would make sense to add 3 instead of dividing by 2 even though we are at an even number.
Log in to reply
That's what I did too. Working backwards but always accounting for both possible steps. This shows the "feeder numbers" which work, and we can also see why 7 is the minimum.
I see. Thanks, I didn't see much of it and just rammed my way through. I just got lucky for this question, I guess.
Nice logic! :-)
I don't think this actually works, because the very last operation (to get from 25 to 11) is adding 3 to an even number: 25 + 3 = 28 ; / 2 = 14 ; / 2 = 7 ; + 3 = 10 ; / 2 = 5 ; + 3 = 8 ; + 3 = 11 Following the stated rule, you would end in an infinite loop: ... 5 ; + 3 = 8 ; / 2 = 4 ; / 2 = 2 ; / 2 = 1 ; + 3 = 4 ...
Relevant wiki: The M2S3 Game
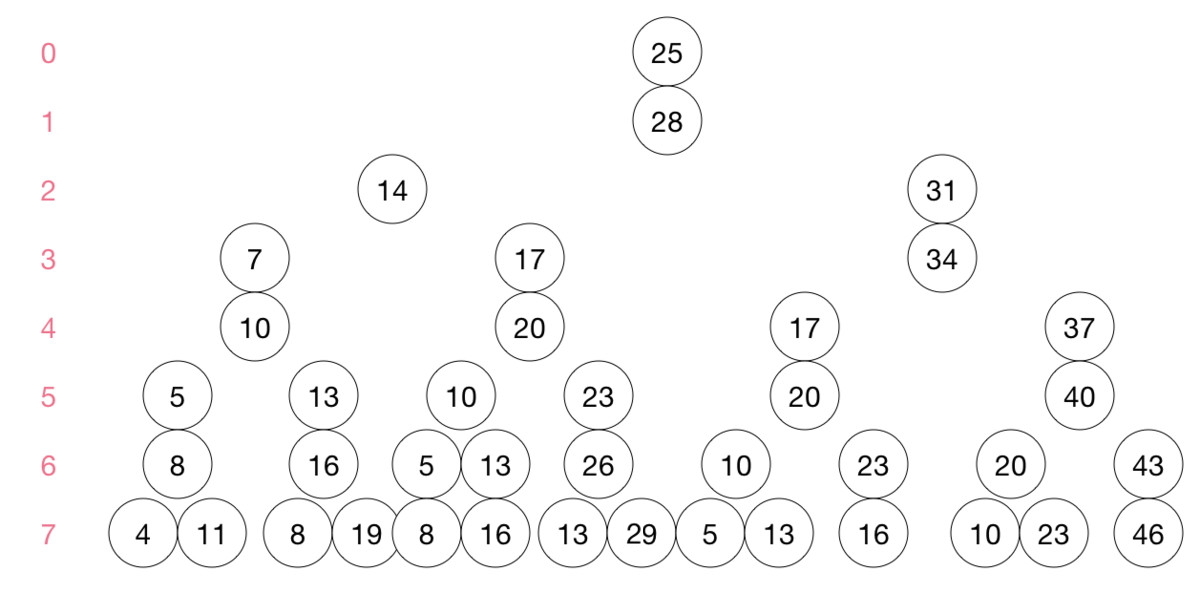
Working backward: to have 2 5 in step 0,
step 1 must have 2 8 ,
step 2 must have 1 4 or 3 1 ,
step 3 must have 7 , 1 7 , or 3 4 ,
step 4 must have 1 0 , 2 0 , ( 1 7 ), or 3 7 (we ignore 1 7 because we already found a quicker way from 1 7 to 2 5 ),
step 5 must have 5 , 1 3 , ( 1 0 ), 2 3 , or 4 0 ,
step 6 must have 8 , 1 6 , 2 6 , ( 2 0 ), or 4 3 ,
step 7 must have 4 , 1 1 , ( 8 ), 1 9 , ( 1 3 ), 2 9 , or 4 6 ,
and we see that 1 1 can lead to 2 5 in no less than 7 steps.
Output: