Get Going
If A P = A C + 2 ⋅ C B , what is the measure ∠ A B P in degrees?
The answer is 110.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
i did something similar too,gimme high five
Nice! How did you think of filling this out?
all most there
Omar you are mad Mexican
Are you kidding bro?I can't believe a 13 years old teenager able to solve this,awesome!
Log in to reply
Log in to reply
Keep on improving!
No I'm not,just quite surprised hehe :) ;) ;)
what can't ? if they can solve IIT question paper
Log in to reply
Well,nothing bro...you definitely can do it too bro :) ;) ;)
nice elegant solution ;)
Here's my solution: what's wrong with it?
Thanks! I have updated the answer to 110.
In future, if you spot any errors with a problem, you can “report” it by selecting the “dot dot dot” menu in the lower right corner.
Log in to reply
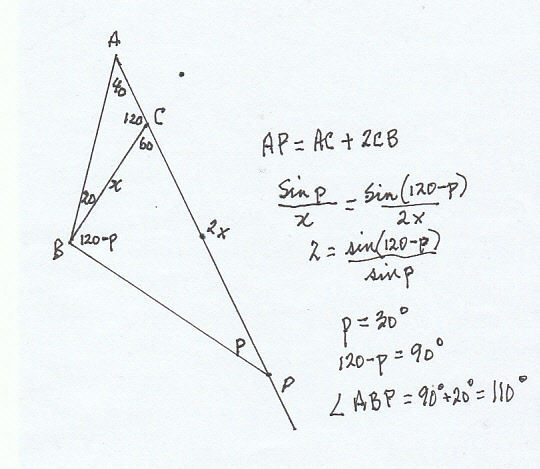
Sir, i used the cosin rule on the angle 60 in the triangle BCP to get : BP=the rout of 3 times CB.then used the sin rule on the triangle ABC to get: AC=0.532CB.Therefore:AP=AC+CP=2.532CB.Then I used the sin rule on the triangle ABP where:BP/sin(40)=AP/sin(ABP),and i got (ABP=70).Is my solution right and this problem has two probabilities.
Log in to reply
sin A B P = B P A P ∗ s i n 4 0 = 3 C B 2 . 5 3 2 C B ∗ s i n 4 0
∵ sin θ = sin ( 1 8 0 − θ ) ⇒ ∠ A B P = 7 0 ∘ o r = 1 1 0 ∘
Then we must test which one satisfy other relations in the problem.
Proof:
The triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side.
In △ A B C
⇒ A B < A C + C B ⇢ 1
∠ A B P = 7 0 ∘ o r = 1 1 0 ∘ If ∠ A B P = 7 0 ∘ ⇒ ∠ P = 7 0 ∘
⇒ △ A B P is isosceles triangle A B = A P .
∴ A B = A P = A C + 2 C B ⇢ 2
But 2 contradicts 1 ⇒ ∠ A B P = 1 1 0 ∘
Another Proof:
In △ C B P
C P > C B ⇒ ∠ C B P > ∠ P ⇢ 1
If ∠ A B P = 7 0 ∘ ⇒ ∠ C B P = 5 0 ∘ , ∠ P = 7 0 ∘ ⇒ ∠ C B P < ∠ P ⇢ 2
But 2 contradicts 1 ⇒ ∠ A B P = 1 1 0 ∘
Hint
After you get that B P = 3 C B
As C B = 1 C B , B P = 3 C B , C P = 2 C B ⇒ Ratio 1 : 3 : 2
⇒ △ B C P is a 3 0 − 6 0 − 9 0 triangle ⇒ ∠ C B P = 9 0 ∘
⇒ ∠ A B P = 2 0 + 9 0 = 1 1 0 ∘
Log in to reply
@Mustafa Embaby – Thanks a lot for your efforts,brother.nice proof ;)
If you draw the diagram then you would realize that you obtained the reference angle. The real angle is 180 - 70 which equals 110.
not trying to be rude but using sines and splitting CBP was pretty unnesecary.Hopefully you didn't think this was rude
We were given that A P = A C + 2 C B .
Obviously we know that A P = A C + C P .
So we can see that C P = 2 C B .
So the ratio C P : C B is 2 : 1 .
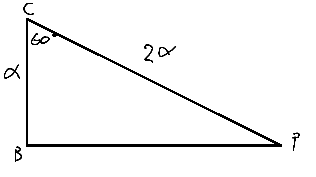
So I immediately recognized it as 30-60-90 triangle.
Therefore ∠ C B P is 9 0 ∘
And from what we were given, we can tell that ∠ A B C = 2 0 ∘
So ∠ A B P = ∠ A B C + ∠ C B P = 2 0 ∘ + 9 0 ∘ = 1 1 0 ∘
That's how I solved it as well.
same for me.
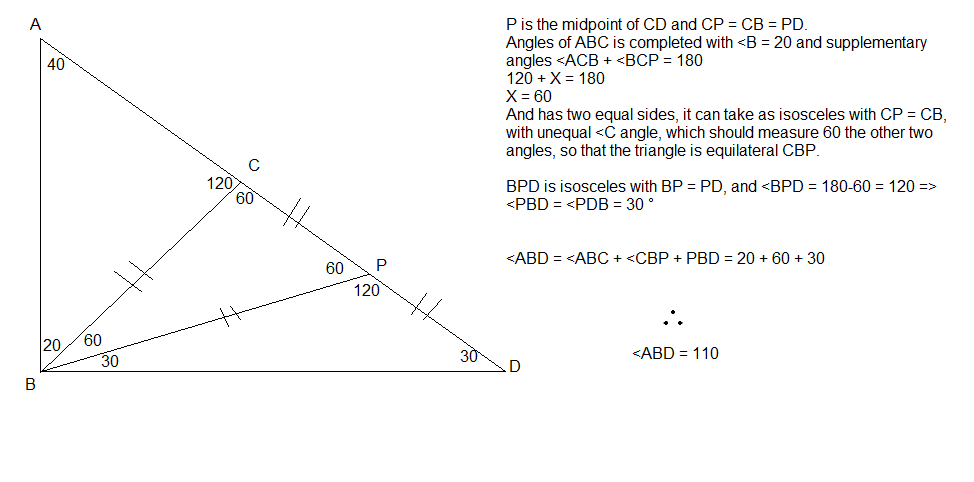
Let D be the mid point of line segment CP.
Draw a line joining B to D.
Since CB = CD and Angle BCD = 60, therefore BCD is equilateral triangle.
Hence BD = CD = DP.
Since BD = DP, therefore BDP is isosceles triangle.
Since Angle CDB = 60 (BCD is equilateral triangle), therefore Angle BDP = 120.
Hence Angle DPB = 30 (BDP is isosceles triangle).
Angle ABP = 180 - 40 - 30 = 110
since
AP = AC + 2 CB
Then
CP = 2 CB
Let CB = x, then CP = 2 x
In triangle CPB
(BP)^2 = x^2 + (2x)^2 - 2(x)(2x) cos 60 ............(cosine law)
(BP)^2 = 3 x^2
sinse
(BP)^2 + (BC)^2 = 3 x^2 + x^2 = 4 x^2 = (BP)^2
Then
angle CBP = 90
In triangle ACB
angle ABC = 180 - (120 + 40) = 20
Then angle ABP = 90 + 20 = 110
thanks sir, i was able to follow your step perfectly and sketch it out,
From the smaller triangle, we know that the missing angle is 2 0 ∘ . Now we have to find ∠ C B P . We also know that ∠ B C P = 6 0 ∘ . Additionally from the given statement, A P = A C + 2 ⋅ C B , which implies that 2 C P = C B . Since the ratio of the angles is 2 1 , and the included angle is 6 0 ∘ , we know this is a 3 0 − 6 0 − 9 0 ∘ triangle, which means ∠ C B P = 9 0 ∘ . Now, 2 0 ∘ + 9 0 ∘ = 1 1 0 ∘ , and that is the answer.
We can notice that CBP° is 90°. and since we know the 180=x+120+40. So x=20° So B=x+90 =110°
AP-AC=CP.CP=2BC.Thus CBP IS A 30-60-90 triangle where angle CBP is 90 degrees.Since angle ABC is 20,angle ABP is 110
Drop a perpendicular on CP namely BD from B.We know,CP=2CB.Let CP=4a and CB=2a.As angle BCD=60 ,CD=a and BD=((3) 1/2)a. So DP=3a and tan(DBP)=3 (1/2),giving angle DBP=60 .Already angle CBP=30* and angle ABC=20 ,so angle ABP=(60+30+20) =110*.
A/sina=B/sinb A =2B 90 and 30