Gianlino's Disc
Three points are randomly chosen from the interior of an unit circle.
The probability that the circumcircle passing through those three points lies entirely inside the unit circle can be expressed as B A , where A and B are co-prime integers.
Find A 2 + B 2 .
This problem is not original, credit goes to "Gianlino". A proof of this would be nice.
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Michael Mendrin I've been waiting for you to post this question, since you were the one to originally ask it on Y!A. You may recall that I posted the same question there years after you did, not knowing its "history", so although I always wanted to post the question myself I felt that you had the honors.
If this problem doesn't end up at a 400 point level I will be surprised, and if someone comes up with an alternative solution I will be impressed, to say the least.
Log in to reply
There's actually more complicated history behind my "asking" this problem on Y!A, since gianlino had originally posed it it earlier and I solved it. But, yeah, gianlino's solution was the Mother of Solutions that I've ever seen posted on Y!A. If gianlino ever comes to Brilliant, we'll have to have a level six.
Log in to reply
More complicated? Oh, o.k.. Anyway, I asked it since to me it seemed like a natural question to ask; little did I know how difficult it actually was.
This was the solution of gianlino's that finally left no doubt in my mind that he was a genius.
Log in to reply
@Brian Charlesworth – I too didn't solved this problem on my own, i saw this problem almost a year before on AoPS, with no solution. Answer was given there, but there was no solution. You just can't solve this without using C++/Python. Gianlino proved that its 2 / 5 . To find 2 / 5 is more hard. I believe that this problem should asked in discussion, rather than posting it as a problem.
Log in to reply
@Shivang Jindal – That's a fair point, but I think it will get more attention as a posted problem rather than note/discussion. It doesn't look like it should be as difficult to solve analytically as it actually is; that's part of its beauty.
I can't speak for Michael, but I think it's o.k. to have one problem posted on Brilliant that is pretty much impossible to solve analytically. I keep thinking that there must be a simpler solution, and who knows, maybe one of the young, future "gianlinos" on this site will come up with such a solution. :)
Log in to reply
@Brian Charlesworth – I agree. My math instincts tell me that if a problem has a "simple" answer, there ought to be some "simple" proof as well. But this one defies an easy proof, and that's the mystery of it.
@Shivang Jindal – That's interesting, it was on AoPS "a year ago"? gianlino and I tackled this problem on Y!A over 4 years ago. He has a fondness for these kinds of problems. Yes, it can be solved without using C++/Python, etc.
Log in to reply
@Michael Mendrin – Actually i tried this problem , for more than 3 hours then left. That;s why i remember :)
Did the one who dispute my latter problem was you? If so, well, I got the problem from A Treatise on the Integral Calculus Volume 2, a book by Joseph Edwards (1854–1931). Anyway, I post his answer here where I copy from his book. Have a look.
Log in to reply
@Tunk-Fey Ariawan – Yes, it was me, and I suspected that you found the problem and its solution from some hoary old book. This is one of those classic cases in mathematics where it all depends on what does it mean to make a random selection of points, such as Bertrand's Paradox, or Charles Dodgson's acute triangle problem. You get different answers depending how points are "randomly selected".
THIS IS NOT MY SOLUTION, this is copy pasted from yahoo answers. I'm in the process of latexing it to make it easier to read.
Let E is be set of triples ( A , B , C ) such that the circumcircle lies in the unit disc D = D ( O , 1 )
We want to show that int_E dA dB dC = (2/5) pi^3
Let R the radius of the circumcircle of ABC and G its center.
We fix A and we change variables. We suppose that B,C have polar coordinates ( r b , t b ) , ( r c t c ) with A at the origin. So r b = A B and r c = A C , t b = ( A x , A B ) , t c = ( A x , A C ) .
We are going to change variables and use G, s b = ( G x , G B ) , s c = ( G x , G C ) as the new variables, G having polar coordinates ( r g , t g ) still with A at the origin.
Let's compute the Jacobian going from ( r b , t b , r c , t c ) to \((R,t_g,s_b,s_c)\ )
We have the following formulas, in which we don't need to worry about signs since we'll only use the absolute value of the determinant. They follow from the half-angle property in the circle
\(r_b = 2 R \sin{\dfrac{t_g + pi - s_b}{2}} = 2 R \cos{\dfrac{t_g - s_b}{2}}\)
r c = 2 R cos 2 t g − s c
t b = 2 t g + p i + s b + 2 π = 2 t g + s b + π
t c = 2 t g + s c + π .
The partial derivatives are
\color\green{2 \cos{\dfrac{t_g - s_b}{2}}, - R \sin{\dfrac{t_g - s_b}{2}}, R \sin{\dfrac{t_g - s_b}{2}},,,,,,,,0}
2 cos 2 t g − s c , − R sin 2 t g − s c , , , , , , , , , 0 , , , , , , , , R sin 2 t g − s c
,,,,,,,,,0,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,1/2,,,,,,,,,,,,,,,,,,,,,,,,,,,1/2,,,,,,,,,,,,,,,,0,,,,,,,,,,,,,,,
,,,,,,,,,,,,0,,,,,,,,,,,,,,,,,,,,,,,,,,,,,1/2,,,,,,,,,,,,,,,,,,,,,,,,,,,,0,,,,,,,,,,,,,,,,,1/2,,,,,,,,,,,,,,,
The Jacobian is R sin 2 s b − s c = 2 B C
So d B d C = A B ∗ A C d r b , d t b , d r c , d t c
⇒ R ∗ A B ∗ A C ∗ B C / 2 d R , d t g , d s b , d s c
⇒ A B ∗ A C ∗ B C / 2 d G , d s b , d s c where in the final line we switch back to Cartesian coordinates for G.
We now exchange the order of integration, fix G and take A in polar coordinates with G as the origin.
Then A B × A C × 2 B C d A , d G , d s b , d s c
becomes A B × A C × 2 B C d R , d G , d s a , d s b , d s c .
We turn to polar coordinates in G. Set r = O G and g = ( O x , O G )
We simplify s a , s b , s c in ( a , b , c ) and we are reduced to
2 8 ∣ sin 2 a − b sin 2 b − c ∣ sin 2 c − a R 3 × r d R , d r , d g , d a , d b , d c
with the conditions r > 0 , R > 0 and r + R < 1 , and ( a , b , c , g ) in [ 0 , 2 π ] .
(R,r) and (a,b,c,g) can be separated.
The integral in (R,r) gives 1/120.
We set u = a − b , and v = b − c . The angular integral can be written as
∣ sin 2 u sin 2 v sin 2 u + v ∣ d g , d a , d u , d v .
The variables a and g can be pulled out giving a factor 4 π 2 .
So far we have ( 2 4 0 8 ) × 4 × π 2 = 1 5 2 p i 2 .
So we are left with showing that
∫ 0 2 p i ∫ 0 2 p i ∣ sin ( u / 2 ) sin ( v / 2 ) sin ( ( u + v ) / 2 ) ∣ d u , d v = 3 p i
which is straightforward.
edit The 2 bottom lines of the Jacobian got cut. They are (0,1/2,1/2,0) and (0,1/2,0,1/2)
Log in to reply
I dont know how to edit the third line, third to last line, and 4 lines beneath the green row due to the fact that I don't know what they're asking. Is int interval or integral. and the commas part, is that supposed to be a Matrix?
with 0,1/2,1/2,0
0,1/2,0,1/2
0,1/2,1/2,0
0,1/2,0,1/2
For what it's worth, I'll share this answer here as an alternative answer, where the result is slightly different from this OP. This answer is derived by Joseph Edwards (1854–1931) in his book: A Treatise on the Integral Calculus Volume II page 817-818. Here is his answer:
 Circle in Circle 1
Circle in Circle 1
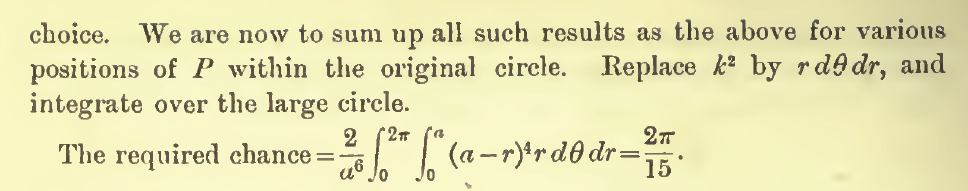 Circle in Circle 2
Circle in Circle 2
Indeed, using Monte Carlo simulation the probability is ranging over the interval 0 . 3 9 9 9 to 0 . 4 0 0 9 7 which nicely agrees with Michael's OP answer, 0 . 4 . But comparing this interval with Edwards' answer: 0 . 4 1 8 8 7 9 , leaves me with a feeling of concern. Why there is a disagreement between his answer and simulation of about 5 % ? I don’t know. Something is not quite right here. Interestingly 5 2 = 1 5 / 3 2 is almost equal to 1 5 2 π = 1 5 / π 2 But that’s simply making-up from me. ⌣ ¨
I can tell you that it is exactly 0.40000... = 2/5, which is the surprising result for this problem. Goodness knows that I've spent enough time with gianlino, who originally proposed this problem and originally gave a full solution of it, part of which you see above. He's actually written a paper on it, but unfortunately, he's in France, and I don't know where he is or how to contact him. Let me study the solution you've posted and see if I can see the difference in the way the points are selected. Remember, in those days, they didn't have the benefit of computers to do a Monte Carlo to check their own work.
Yes, okay, that didn't take long at all. The flaw with this old proof is that it starts with a random circle that "wholly fits inside" the larger circle, and then computes the probability of the 3 random points being within its circumference that has an infinitesimal thickness, and you do this for all radii and all possible locations of this circle. This will not yield a truly uniform random selection of 3 points inside of the larger circle. This kind of problem can be VERY tricky, and I've noticed that it's one of the most common ways for people to go wrong in geometrical probability theory, even mathematicians.
I'm really glad that you've brought this old problem and "solution" to attention, because it illustrates the difficulty and importance of the problem of making proper "random selections". Even here in Brilliant, I've seen problems that were incorrectly solved because of mistaken assumptions about random selection.
Log in to reply
As what I have said in my answer, " Something is not quite right here. "
Since your answer matches up numerically, I think I must admit that your answer is correct and I should delete my OP then, LOL.
Ya, I agree with you. The Monte Carlo simulation is a technique that in the pre-computer days of the 1920s Edwards could only have imagined in a science fiction fantasy.
Anyway, I'll take a long break from Brilliant.org or any other online forums. So, if you can contact gianlino using his Yahoo email address and can get his paper on this problem, please share with me. Just send to my Yahoo email. Thanks Michael...
Exaclty, I solved this question using the method shown in the page, posted by Tunk-Fey Ariawan, kept wondering why I am getting π in my answer.
Anyways this is an extremely good problem.
Since the credit for the problem goes to gianlino, it seems fitting that his solution should speak for itself. :)