Square Inception

Draw 2 diagonals in the bigger square:

We find 16 congruent triangles, of which 4 are shaded. So the answer is $\frac{4}{16} = \frac{1}{4} = 0.25.$

Divide the figure into four parts. Appreciate the symmetry. (It's easy to see that the shaded square is has the same area as each of the four parts.) Thus, the answer is $\frac{1}{4} = 0.25.$

enter image description here

By Pythagoras theorem each square is half of the one around it. Hence , 1/2 x 1/2 = 1/4

This one was quite hard for me, considering that there was nothing explicitly stating that any of those figures are squares. Eventually, I gave up and assumed that that is what they were. Now, to the problem itself:

$s_1$ is the side length of the first square.

$s_2$ is for the second square.

$s_3$ is the third.

The length of one side of the second square is obviously equal to a diagonal in the first (Imagine making the diagonal, and sliding it down to the side of the second square) The diagonal of a square is equal to $s\sqrt{2}$ , since it creates a 45-45-90 right triangle, and the diagonal is the hypotenuse, so then $s_1\sqrt{2}=s_2$ . By that same logic, $s_2\sqrt{2}=s_3$ .

Assume $s_1=1$ . Plugging that into our equations, that would mean $s_2=\sqrt{2}$ , and $s_3=2$ .

$a_1$ is the area of the first square.

$a_2$ is for the second square.

$a_3$ is the third.

Using the corresponding side lengths, we can conclude:

$a_1=1$

$a_2=2$

$a_3=4$

Say we shade $a_2$ . Then, the fraction of the diagram that is shaded is $\frac{a_2}{a_3}=\frac{2}{4}=\frac{1}{2}$ . The fraction of $a_2$ that is shaded by $a_1$ is equal to $\frac{a_1}{a_2}=\frac{1}{2}$ .

Therefore, in order to get the amount of $a_3$ that $a_1$ takes up, we multiply $\frac{a_2}{a_3}*\frac{a_1}{a_2}=\frac{1}{2}*\frac{1}{2}=\frac{1}{2*2}=\frac{1}{4}=0.25$

Therefore, our answer is $\boxed{0.25}$ !

Easy one is mid point theorem.If we join all the mid points of a square,then the square obtained has area equal to half of the bigger one.

Considering the bigger square,take its each side as 2a..(i.e, a+a) & start solving.

SIMPLE SOLUTION

Let 1 triangle of the second largest square be a 1, now you can easily deduct that the area of the shaded square is 4. The area of one of the triangles of the largest square is then 2. (2+1)*4 + 4 = 16 So, 4/16 = 1/4 = 0.25

P.S. Thank you for reading.

For this we just need a little common sense the area of the square inside is half of the first similar in nest case so half of half is quarter

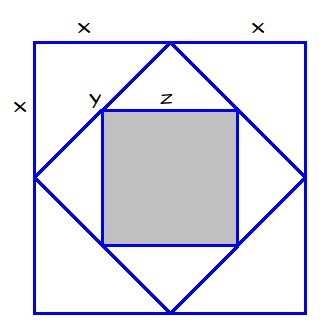Consider my diagram. Using the pythagorean theorem, we have

$y=\sqrt{x^2+x^2}=x\sqrt{2}$

It follows that $\dfrac{y}{2}=\dfrac{x\sqrt{2}}{2}$ .

Use pythagorean theorem again.

$z=\sqrt{\left(\dfrac{y}{2}\right)^2+\left(\dfrac{y}{2}\right)^2}=\sqrt{\left(\dfrac{x\sqrt{2}}{2}\right)^2+\left(\dfrac{x\sqrt{2}}{2}\right)^2}=x$

The ratio of their areas is

$\dfrac{A_1}{A_2}=\dfrac{x^2}{(2x)^2}=\dfrac{x^2}{4x^2}=\dfrac{1}{4}=$ $\boxed{0.25}$

You can shift the shaded square to the top left (or every other) corner of the biggest square. And while doing so, you see that the corners of the shaded square are moving parallel along on two sides of the diagonal square. Since the corners of this diagonal square mark the midpoint of the biggest square's sides, the sidelength of the shaded square is half of the sidelength of the biggest square. Therefore the areas ratio is 1:4.

Draw 2 diagonals in the bigger square We find 16 congruent triangles,in which 4 are shaded. So, 4/16 =1/4 =0.25

Since I didn't have any other way to solve the problem, I solved the problem by plugging in values for the squares. So.....

I plugged in that the outer square had an area of 64 square units, thus an 8 by 8 square.

The second one would have a diagonal length of 8 because the diagonal stretches as far as the bigger squares side length.

I found out that from the edge of the square to the center of the smallest square is 4.

That means that the smaller square has an "edge to center" length of 2.

That means that the side length of the smallest square is 4 and 4 * 4 is equal to 16.

Bigger square area: 64 Smaller square area: 16

16/64 = 0.25 So the answer is 0.25

http://ppt.cc/b5Dqt

See the url for the picture that has the supporting line (red) that explain the answer very easily. Calculation: (shaded area / largest square area) = 4/16 = 0.25

I tried to input 1/4 and coud not, when I was asked to write a number. But 1/4 is the way I use to write fractions. Then I tried with 4 (meaning 4th part), but that is obviously a wrong answer. I suggest adding the possibility to write fractions. Numbers like 1/3, for instance, cannot be written in a decimal form.

In which angle this problem has been reported??? :-o