Give me ID Card-2!
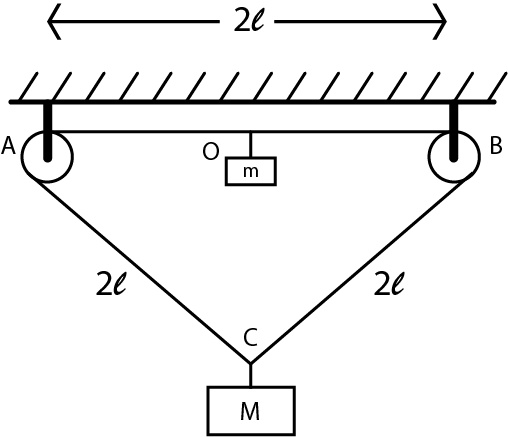 A triangular loop
A
B
C
of light string is passed over two small frictionless pulleys A and B
(
A
B
=
B
C
=
A
C
=
2
l
)
A triangular loop
A
B
C
of light string is passed over two small frictionless pulleys A and B
(
A
B
=
B
C
=
A
C
=
2
l
)
Two masses m and M are attached at the midpoint O of A B and at point C , respectively. If m is released, m & M cross each other at any point P as shown in the figure. Find the minimum value of M m so that they cross each other.
The answer is 0.54919338.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
This is a glorious solution. Excellent diagram, and thoroughly explained. Can you think of a way to solve this without forces?
Please do post these type of questions.I like them a lot man. @Kishore S Shenoy
@Brilliant Physics : How can you do it without considering forces or Energy?
@Kishore S Shenoy nice solution :). I couldn't solve it but enjoyed the solution!
Log in to reply
Thanks! Keep doing questions until you are able to do it!
Yet another beautiful application of energy conservation :-)!I think I saw this problem somewhere...where did you get it?
Can u explain why the length AP=3/2 L
Log in to reply
Oh! Sorry for the late response, internet was down.
So, What is the initial length of the string? 2 ℓ × 3 = 6 ℓ . So, when it is dived into four parts, the length becomes, 4 6 ℓ = 2 3 ℓ . I hope I am clear!
@Kishore S Shenoy How have you compared the change in potential energies of the two blocks?
Log in to reply
In the sense?
Log in to reply
You have written that change PE of mass m > change in PE of M - how does that come?
Log in to reply
@Kriti Verma – The bodies will cross only if the system has kinetic energy at the crossing point. Hence, if the change in potential energy is negative at point of crossing, the system has kinetic energy will proceed forward.
@Kishore S Shenoy can you please explain |∆U(m)|>|∆U(M)| ?
Log in to reply
Since the small mass has to come down, the change in potential of the system due to the smaller mass should be larger than the change in potential of the heavier mass. Here, small refers to small letter m and large, M.
How to solve this problem is solved by force concept
This problem is in our FIITJEE study material.. Thanks for such a beautiful solution :)
Log in to reply
can you explain why ∆U(m)>∆U(M) plz. Fellow FIITJEEan here i am not able to comprehend with it.
Log in to reply
Because nature seeks for the least energy state. Motion is possible, therefore, only if the change in energy is negative.
Log in to reply
@Kishore S. Shenoy – i still did not understand could you explain it in a different way why why ∆U(m)>∆U(M) ?????
Log in to reply
@Aryan Bansal – Okay, I see where you may be coming from.
I'm not stating that Δ U [ m ] > Δ U [ M ] . My argument is that, if the masses have to cross, then the total change in energy of the system must be negative. That, in turn, would mean, the gain in energy must by the bigger block must be less than the loss in energy of the smaller block. That way Δ U sys = − ∣ Δ U [ m ] ∣ + − ∣ Δ U [ M ] ∣ < 0 . This gives you the required inequality.
why is potential energy of m > M??????
can you explain why the change in potential of the M block is Mg(sqrt(3) -sqrt(5)/2)l
Log in to reply
It's initial height is 3 l from top and final is 2 5 l . Thus the change is M g ( 3 − 2 5 ) l .(Take magnitudes ⋯ )
Log in to reply
Thanks. Nice solution
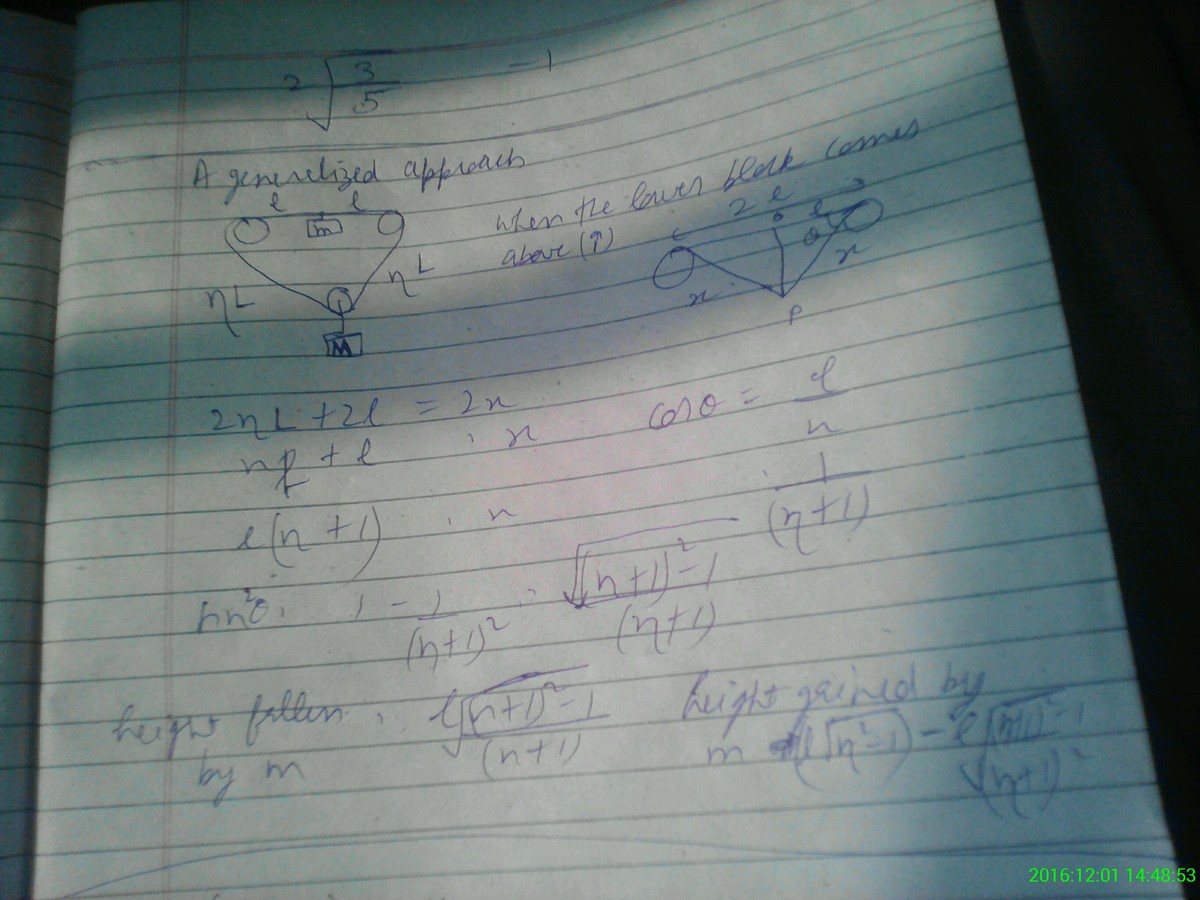 so the final generalised form you get will be
M
m
≥
2
η
+
3
η
+
1
−
1
so the final generalised form you get will be
M
m
≥
2
η
+
3
η
+
1
−
1
m/M>1 , just by using force balance
Can you please type it down, couldn't understand a thing. Would be helpful!
Why is AP=(6/4)l
The length of the string is 2 l × 3 = 6 l At their crossing point P, the length of the string connecting both the blocks will be equal
⟹ Length of the sting connecting the one of the block from one of the pulleys
A P = 4 6 l = 2 3 l
But the length between the pulleys remains same ( = 2 l )
Let θ = A B P
∴ cos θ = 3 2
⇒ sin θ = 3 3 2 − 2 2 = 3 5
O P = B P ⋅ sin θ = 2 3 l × 3 5 = 2 5 l
Now, for the two blocks to cross each other,
∣ △ U ( m ) ∣ > ∣ △ U ( M ) ∣
⟹ m g 2 5 l > M g ( 3 − 2 5 ) l
since l > 0 and g > 0 ,
m 2 5 > M ( 3 − 2 5 )
⟹ M m > 5 2 3 − 5
∴ M m > 0 . 5 4 9 1 9 3 3 8