Give me ID card!
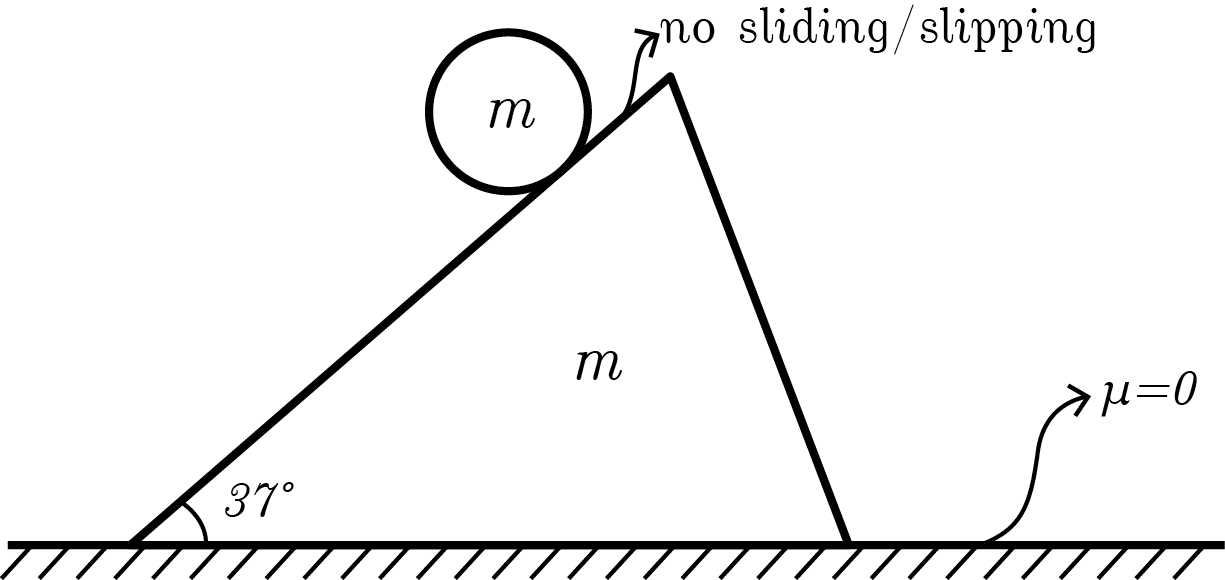 A solid metallic sphere of mass
m
and radius
R
is free to roll (without sliding) over the inclined surface of a wooden wedge of equal mass
m
. Wedge lies on a smooth horizontal floor. When the system is released from rest, find the force
f
between sphere and wedge.
A solid metallic sphere of mass
m
and radius
R
is free to roll (without sliding) over the inclined surface of a wooden wedge of equal mass
m
. Wedge lies on a smooth horizontal floor. When the system is released from rest, find the force
f
between sphere and wedge.
If f = k h m g , give your answer in the form of h k + h + k
The answer is 15.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Would you please give the whole solution on how you got those numbers?
Log in to reply
That will be tough. There are slightly large numbers (4 digit) involved. Are you sure you want it?
Log in to reply
Definitely! ⌣ ¨
4 digit numbers ... how ?
Brilliant problem!! really enjoyed it
@Miguel Vásquez Vega and @Anirban Mandal ... here's my solution :)
Log in to reply
Why have you stopped posting ur cool mechanics problems? and you haven't posted more binomial summations also i am waiting for them :)
Log in to reply
I had {Exams} + {No Internet} (internet connectivity problem). So I had to stop :).
Hey can you tell me a way to learn latex? your latex skills are awesome!
Log in to reply
Just read the Wikipedia Page of Latex. It's awesome!
Thanks! Question: can you apply Newton's second law on the sphere w.r.t. the non- inertial frame the wedge is on?? As long as I understand, you would have to consider another inertial force acting on the sphere due to the wedge's acceleration...
Log in to reply
Well, that's why I included pseudo accelerations... see those f cos θ and N sin θ acting in opposite directions to the corresponding accelerations on the wedge.
Log in to reply
@Kishore S. Shenoy – I totally agree now! Nice problem and solution! Thank you very much!
Nice problem! Your solution makes the problem look easy even if it isn't.
I really liked your style of applying the pseudo force directly, i.e. the opposite forces.
Keep up the good work
Log in to reply
Thank you! I appreciate that you appreciate my work!
how did you get this N ( 1 + s i n 2 θ ) = m g c o s θ + f c o s θ s i n θ ⇒ 3 4 N / 2 5 = 1 2 f / 2 5 + 4 m g / 5
Dude what grade where you in when you solved this ,this is insane .Nice job .
Log in to reply
Thanks. I was in my junior year of high school (grade 11).
t h a t a s h o w i d i d i t
Spelling mistake zone ahead.
Forgive me for placing extra-large image right next to a tiny one; I don't know how to change it.
Equating forces on the sphere along the perpendicular of the surface of the wedge , N ( 1 + sin 2 θ ) = m g cos θ + f cos θ sin θ ⇒ 2 5 3 4 N = 2 5 1 2 f + 5 4 m g ⋯ ( 1 )
Also, α = 2 m R 5 f m a = m R α = 2 5 f
Taking forces along the surface of the wedge, N sin θ cos θ + m g sin θ − f ( 1 + cos 2 θ ) = 2 5 f ⋯ ( 2 )
Substituting ( 1 ) in ( 2 ) , 1 4 4 f + 4 8 × 5 m g + 5 1 0 m g = 3 5 1 9 f f = 3 3 7 5 7 5 0 m g = 9 2 m g
∴ f = 9 2 m g