Given Perimeter and Area, Find the Sides

Geometry Level 5

What is the sum of the lengths of the base sides of all isosceles triangles with perimeter 12 and area 5? If there are an infinite number of such triangles, submit -1.

Note: The base of an isosceles triangle is the side with the unique length.

The answer is 7.4915522.

3 solutions

Vinod Kumar
Nov 7, 2020

Solve for triangle a,a,b

2a+b=12, perimeter

(b/2)[a^2-(b/2)^2]^0.5=5, area

Positive Solutions are, 2.0556 and 5.4360

Answer = 2.0556+5.4360=7.4916

David Vreken
Jul 1, 2020

Let the two equal sides of the isosceles triangle be $y$ and the base be $x$ . Then the perimeter is $P = 2y + x = 12$ , which means $y = 6 - \frac{1}{2}x$ .

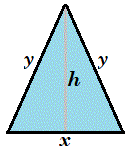
By Pythagorean's theorem, the altitude $h$ of the isosceles triangle from its base is $h = \sqrt{y^2 - (\frac{1}{2}x)^2}$ , so the area is $A = \frac{1}{2}bh = \frac{1}{2}x\sqrt{y^2 - (\frac{1}{2}x)^2} = 5$ .

Substituting $y = 6 - \frac{1}{2}x$ into $\frac{1}{2}x\sqrt{y^2 - (\frac{1}{2}x)^2} = 5$ and rearranging gives $x^3 - 6x^2 + \frac{50}{3} = 0$ , whose solutions can be found numerically to be $x \approx 2.05556985$ and $x \approx 5.43598238$ for $x > 0$ , and $2.05556985 + 5.43598238 \approx \boxed{7.4915522}$ .

By the way, if the area is $A$ and the perimeter is $P$ , then the cubic can be generalized to:

$2P{x}^3 - P^2x^2 + 16A^2 = 0$

No need to memorize. :)

Fletcher Mattox - 11 months, 2 weeks ago

Great equation, thanks for sharing!

David Vreken - 11 months, 2 weeks ago

That's very nice - got me thinking about what choices of $P$ and $A$ actually have solutions, and how many solutions they have. Just to simplify the workings a bit, if we let $x=Pt$ and substitute in, we get $2t^3-t^2+\left( \frac{4A}{P^2} \right)^2=0$ So we'd be interested in how many positive solutions this has. Say $f(t)=2t^3-t^2+K^2$ , where $K=\frac{4A}{P^2}$ .

Now, $f(0)=K^2>0$ and $\lim_{t \to -\infty} f(t) = -\infty$ ; so there is always a negative root.

We have $f'(t)=6t^2-2t$ which means $f(t)$ has turning points at $t=0$ and at $t=\frac13$ . From the shape of a cubic, we know the second of these must be a minimum. If the value of $f(\frac13)$ is negative, there are two positive real roots; if it's positive, there are none.

Finally, $f(\frac13)=-\frac{1}{27}+K^2$ so the critical value for $K$ is $\frac{1}{3 \sqrt{3}}$ . When $K$ is larger than this, there are no positive solutions; smaller, there are two. Unsurprisingly, this is exactly the value of $K$ you get for an equilateral triangle.

Chris Lewis - 11 months, 2 weeks ago

I had the same thought process yesterday and made a question related to it which I hope to post in the future.

David Vreken - 11 months, 2 weeks ago

Eep - would you like me to delete/obscure the comment above to avoid spoilers? We could just link to your question instead.

Chris Lewis - 11 months, 2 weeks ago

@Chris Lewis – No, it's okay. They'll be rewarded if they do some research and find your comment. I probably won't post it until next week, anyway.

David Vreken - 11 months, 2 weeks ago

@David Vreken – Research time! :)

Mahdi Raza - 11 months, 1 week ago

just the same way.

Niranjan Khanderia - 11 months, 1 week ago

A Former Brilliant Member
Jun 30, 2020

Let the lengths of equal sides of the triangle be $a$ each, and that of the base be $12-2a$ ( $a<6$ )

Then $(6-a)\sqrt {a^2-(6-a)^2}=5$

$\implies 12a^3-180a^2+864a-1321=0$

The roots of this equation are $\approx 6.74578,\approx 3.28201,\approx 4.97222$

Of these, the value of $a\approx 6.74578$ , being greater than $6$ , is discarded.

Hence the required sum is

$2(12-3.28021-4.97222)=\boxed {7.49514}$ .

Solution to this problem :

I have tried in this direction

Let the triangle be $\triangle {ABC}$ right angled at $C$ . Let the length of $\overline {BC}$ be $l$

Radius of the circle in the upper half of the triangle is

$r=\dfrac {l\sin A\cos A}{1+\sin A+\cos A}$

Radius of each circle in the lower half of the triangle, which is congruent to the former one, is

$r=\dfrac {l\cos^2 A}{4\sin A\cos A+1+\sin A+\cos A}$

From these we get the equation

$16\cos^5 A+16\cos^4 A-20\cos^3 A-20\cos^2 A+6\cos A+6=0$

Since $A$ is acute we have two eligible roots of this equation :

$A=30\degree,A=60\degree$

Considering the first root we get

$\dfrac rl=\dfrac {\sin A\cos A}{1+\sin A+\cos A}=\dfrac {\sqrt 3-1}{4}$

So, the required ratio is

$8π(\frac rl) ^2\tan A=π\left (\dfrac {2\sqrt 3}{3}-1\right )$

Hence $a=2,b=3,c=1$ , and $a+b+c=\boxed 6$ .

Given Perimeter and Area, Find the Sides

The answer is 7.4915522.

3 solutions

0 pending reports