Glass Half Full?
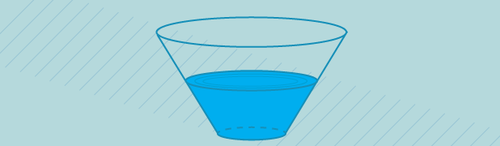Consider a glass in the shape of an inverted truncated right cone (i.e. frustrum). The radius of the base is 4, the radius of the top is 9, and the height is 7. There is enough water in the glass such that when it is tilted the water reaches from the tip of the base to the edge of the top. The proportion of the water in the cup as a ratio of the cup's volume can be expressed as the fraction
n
m
, for relatively prime integers
m
and
n
. Compute
m
+
n
.
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Image
Nice result! But the picture accompanying the problem is very misleading. It took me a while to realize that the cup is a frustum, not a cone. :(
Log in to reply
Yeah, I did my best with the hashed lines and explanation of the variables to the right, but glad that you finally saw it! I was quite surprised at the result when I first derived it as well, especially the final result being independent of the height of the cup.
Log in to reply
The fact that the ratio is independent of the height of the cup shouldn't be that surprising. Remember, we are taking the ratio of the two volumes, and since both of them have the height as a degree-1 term, you would expect it to cancel itself out.
Unrelated, but I got so frustrated by this problem because I kept on getting it wrong. It was my last try when I realized that I counted the imaginary cone at the bottom of the cup in my volume of the water. * facepalm *
Why is using the equation h/3(A^2 + sqrt(A*a) + a^2) to find the volume of the cup and saying that the volume of the water is half cilinder with base "a" and height "h" wrong? I just cant find a motive to think that this is wrong. Someone help please =D. ("a" is the base with radius 4 and "A" is the base with radius 9)
Log in to reply
I can't think of any reasoning as to why that would be the correct volume of water? It could be correct, but your volume of the frustum is off. Double check that. The main insight to solving this problem exploits the fact that the general volume of a cone is 3 1 [ B ] h , where [ B ] is the area of its base and h is its (perpendicular) height, and to recognize that the volume of the water is a slanted cone of water with an elliptical base, with a portion of that cone removed. I had always wondered what the solution would be while drinking a glass of water and seeing that tip of the base, and assumed it'd be an ugly solution, but with that insight turns out to be rather elegant.
The sketch might have helped. The explanation was frustrating.
my idea was the same but i didn't know that a formula for volume of an oblique cone exists..should have googled for it..
.....not so much explaining, I dare say. For example, how one can derive the minor axis of the ellipse? (that had been my big mistake....:-) )
Taking a cross section of the cone, we get an upside town trapezium split into a smaller and larger triangle (the line splitting it is the flat plane when we tilt the cup).
The smaller triangle has base 8 (diameter of base) and height 7 (height of cup); Area1 = 28. Larger triangle has base 18 (top of cup) and Area2 = 63.
The shapes, in two dimensions have the ratio 4:9. In three, this would be 8:27.
Therefore, proportion of smaller section to the whole cup is 8/(8+27) = 8/35. m + n = 43
Your solution is much quicker and simpler than mine, but there is a point I can't get:
How did you find the 3D ratio (8:27) from the 2D ratio (4:9) ?
TIA
Log in to reply
I'm guessing that, in 2 dimensions, you have it as 2^2 : 3^2, so in 3 dimensions, you have 2^3 : 3^3.
Just a thought... I didn't even try on this question, since I have no experience nor have learnt anything involving stuff like this before. It took me quite a while to even understand the question... sigh
great one...
How can you say that the volumes are proportional in a cubic ratio and the areas are similar in a square ratio, known that the solids are not similar?
can you please explain me with a diagram.?
Log in to reply
This is a solid of revolution problem. So you are rotating a 2-D line around an axis to get a solid 3-D shape. In this case you are finding the difference between two solid 3-D shapes. You are going from calculating area to volume. The reason the ratio doesn't remain the same is because the disc slices of the 3-D shapes do not all have the same area as with cyllinders. The disc slices are all circles, so the distances of the lines from the axis are the determining factors in calculating the volume ratio. In calculating the area of the disc slices, these distances are squared. This is why both the numerator and denominator of the area ratio are both squared in determining the volume ratio. I hope that I was somewhat clear, apologize for rambling, and hope I didn't mix up my words. I'm very tired.
Log in to reply
thank you very much.........
I think I can understand what ur saying but there are anomalies with your explanation. since you are explaining this as a rotation problem. think of a cylinder..it is nothing but revolution of a rectangle along it's central axis. now consider 2 rectangles.. dimensions 4 7 and 2 3 or anything else.. the area is 28 and 6 respectively and the ratio would be 6/28 or 3/14. NOw the volumes would be pi 4 7 and pi 1 3.. the ratio of volumes is 3/28.. if your explanation was a generality then it should hold true in this case too.. Why is it not?
Log in to reply
@Rakesh Guduru – cylinder is a rotation of a rectangle along it's central axis..
Looking down the z axis, we see a series of circles with increasing radii, bounded on the left by a vertical line. The idea here is to integrate the area of these circles in order to find the total volume of the liquid.
Firstly, looking at the cross section, the right boundary (hereby referred to as RB) is a line of equation:
x
=
7
5
z
+
2
8
This line serves as both the radius of the circle at an arbitrary value of z and, when looking down along the z axis, the rightmost boundary for our circles' area.
The left boundary (hereby referred to as LB) is a line of equation: x = 7 1 3 z − 2 8 Again, if we look down the z axis, this line serves as the leftmost boundary.
Thus, the volume of the water inside the cup can be expressed as:
v = ∫ 0 7 ∫ L B R B ( R B ) 2 − x 2 d x d z
It would take too much space and time to write out all the steps for solving that integral, but in the end it yields 1 5 1 0 6 4 π
Dividing by the total volume of the frustum and simplifying results in the answer, 8/35. 8+35 = 43