Go Round and Round
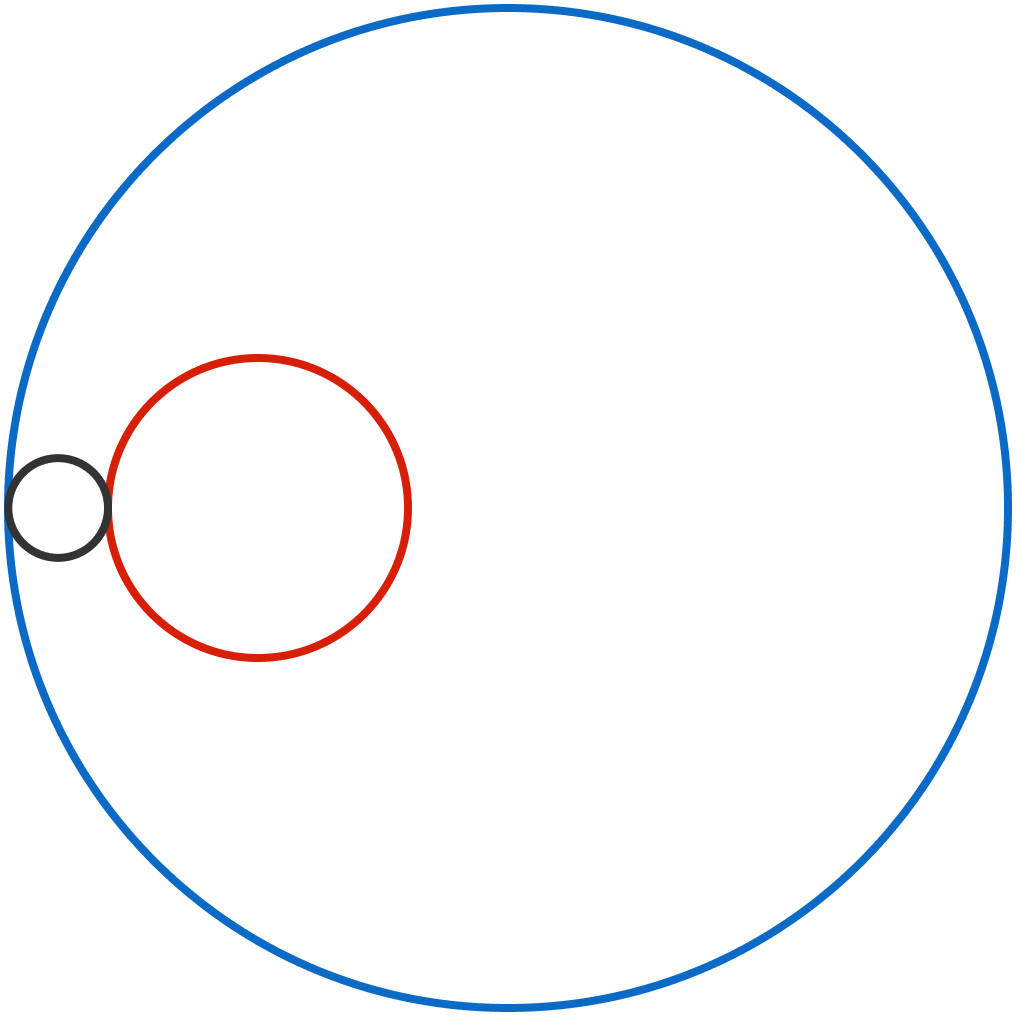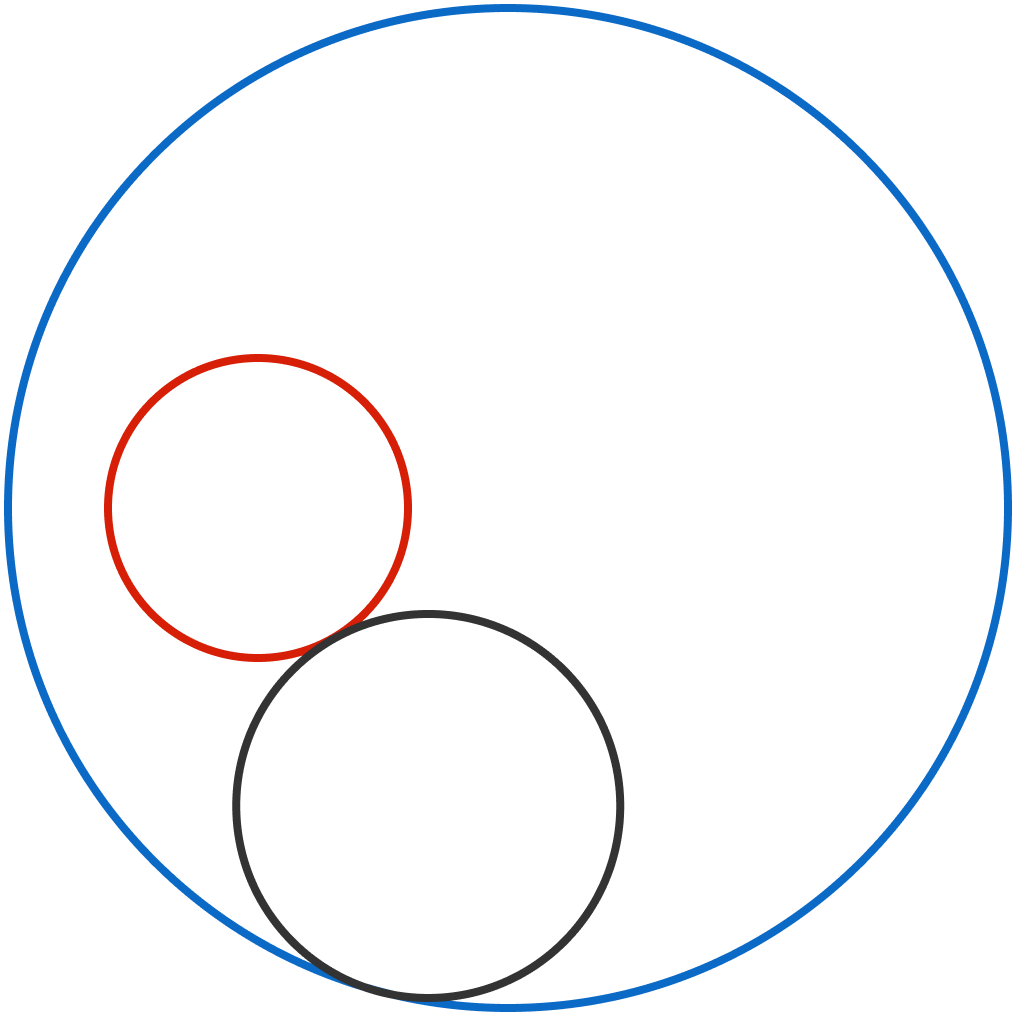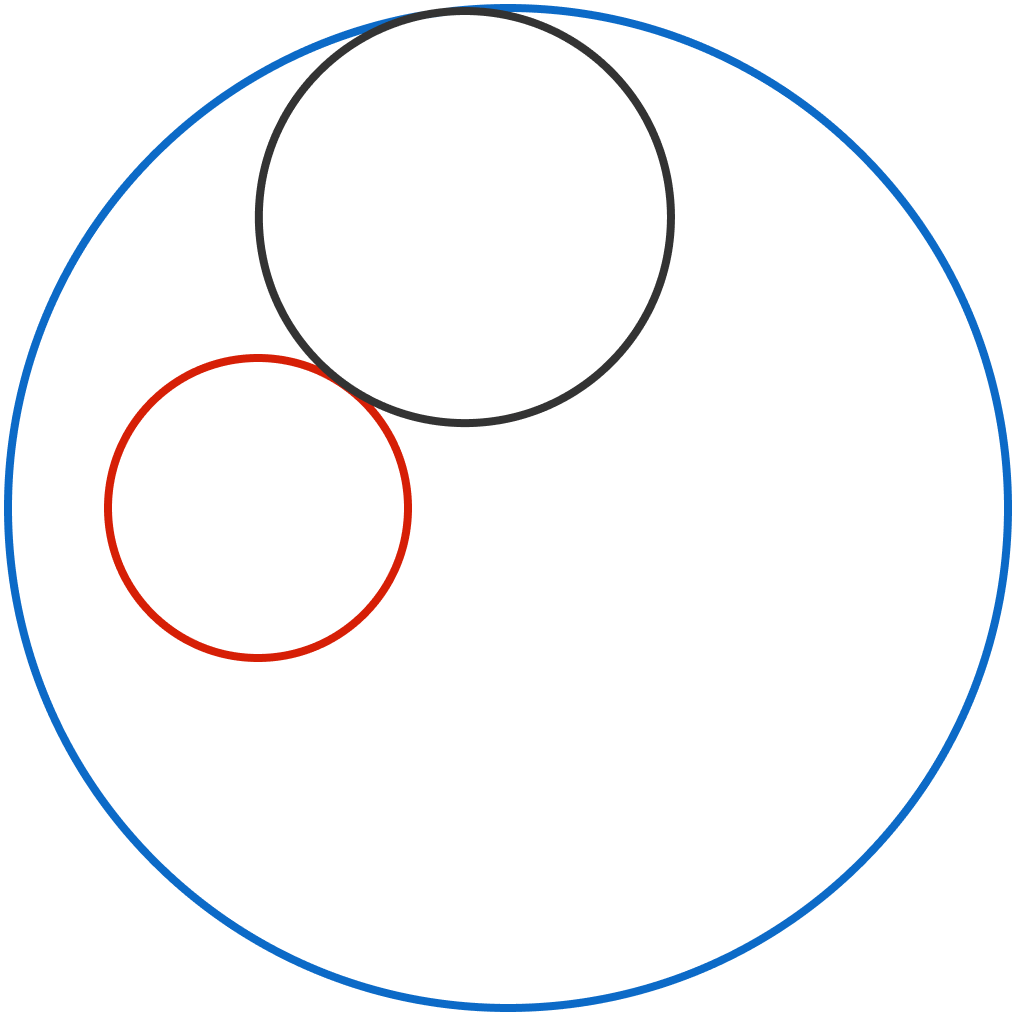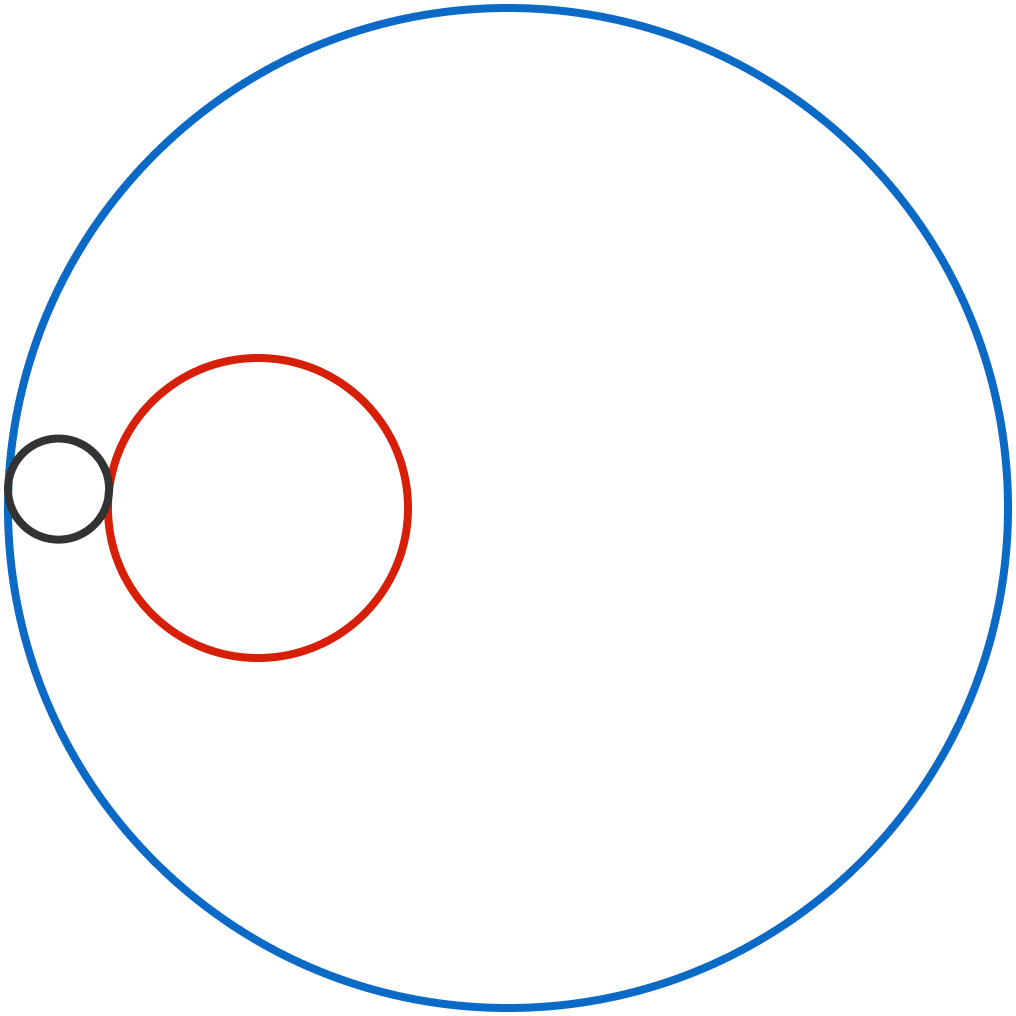
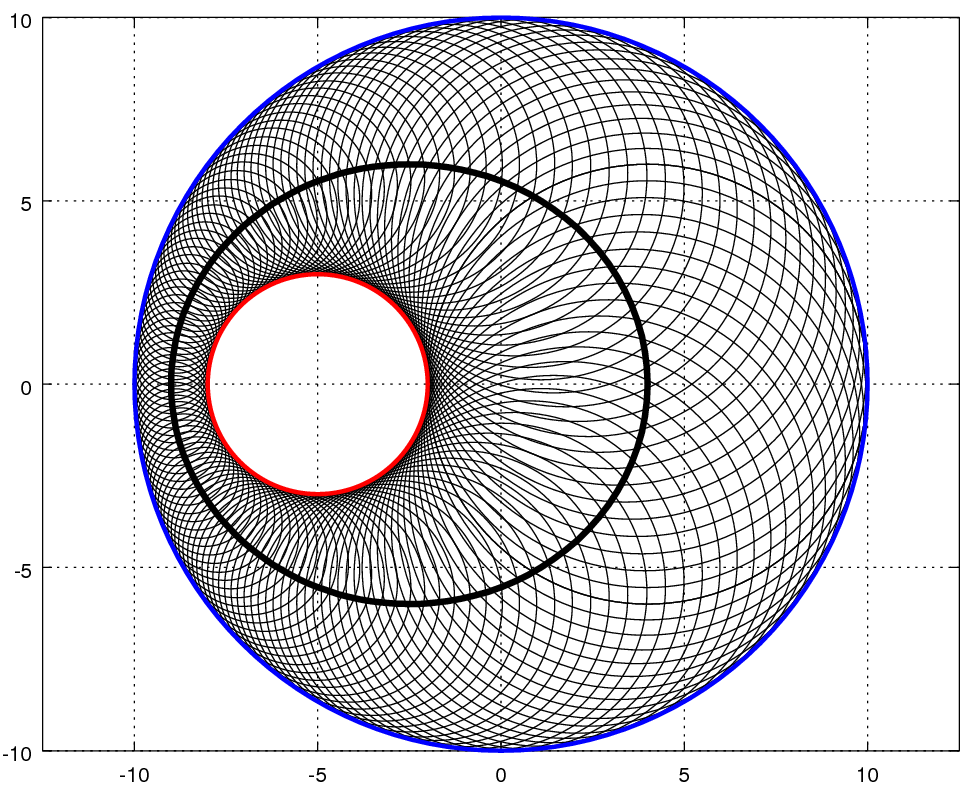
In the figure, the radii of the red circle and the blue circle are 3 and 10, respectively, and the distance between their centers is 5.
The black circle is externally tangent to the red circle and internally tangent to the blue circle. The path traced by the center of the black circles is a closed curve whose area is X π .
What is X ?
The answer is 39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nicely done!
Log in to reply
Thank you very much! How are your JEE preps going?
Log in to reply
Good for math. I still have a lot of chemistry and physics to revise.
Log in to reply
@Akshat Sharda – I have to strengthen my math (with correct time management) and physics. And inorganic chemistry.
Log in to reply
@Tapas Mazumdar – Okay, All the best!
Same method! But I made calculation error and start trying to bash with calculus and got a messy expression. :(
Log in to reply
Calculus? As the solution posted by Mark Hennings? I had learnt some contour integration from youtube but I never used it because there are a lot of things that need to be fully understood like residues and poles before going on the method to solve integral by contour integration.
Log in to reply
Yes, the same solution as Mark Hennings. I made the mistake of assuming that the radii of the smaller circle and variable circle are collinear to both points of tangency, which is not true (one of the points of tangency is, but the other is collinear to the larger circle and the variable circle), and I ended up with a non-elliptical polar expression, which did not evaluate to the correct form of X π . I noticed the mistake and proceeded the way Mark Hennings did, and of course, the results were quite messy with all the complex analysis and things to notice. I ended up solving the integral with desmos.
nice solution!
b^2=(a 1/2)^2-(5 1/2)^2=36
Applying the Cosine Rule, the radius of the third circle in the diagram is r , where ( r + 3 ) 2 = ( 1 0 − r ) 2 + 5 2 − 1 0 ( 1 0 − r ) cos θ and hence r = 1 3 − 5 cos θ 5 8 − 5 0 cos θ
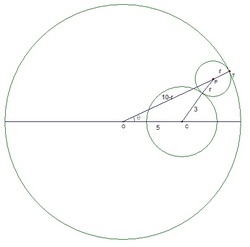
Thus the centre of the third circle has polar coordinates ( 1 0 − 1 3 − 5 cos θ 5 8 − 5 0 cos θ , θ ) = ( 1 3 − 5 cos θ 7 2 , θ ) Thus the desired area is A = 2 1 ∫ 0 2 π ( 1 3 − 5 cos θ 7 2 ) 2 d θ = 2 5 9 2 ∫ 0 2 π ( 1 3 − 5 cos θ ) 2 d θ Making the complex substitution z = e i θ , we obtain A = i 1 0 3 6 8 ∫ ∣ z ∣ = 1 ( 5 z − 1 ) 2 ( z − 5 ) 2 z d z = 2 0 7 3 6 π R e s z = 5 1 ( 5 z − 1 ) 2 ( z − 5 ) 2 z and hence A = 2 5 2 0 7 3 6 π ( d z d ( z − 5 ) 2 z ) ∣ z = 5 1 = − 2 5 ( z − 5 ) 3 2 0 7 3 6 π ( z + 5 ) ∣ z = 5 1 = 2 5 2 0 7 3 6 π × 5 2 6 × 2 4 3 1 2 5 = 3 9 π making the answer 3 9 .
Let A be the center of the blue circle, and let B be the center of the red circle. Let P be the center of the black circle, and let r be its radius. Then A P = 1 0 − r and B P = r + 3 , so A P + B P = 1 3 . Thus, the locus of P is an ellipse. The rest is easy.
Log in to reply
Nice one. I was enjoying the contour integration!
Could someone please explain how the complex substitution is done?
Log in to reply
We have cos θ = 2 1 ( z + z − 1 ) and d θ = i z d z . As θ varies from 0 to 2 π , z runs round the unit circle.
Log in to reply
Still not clear to me.where can I learn about this?
Log in to reply
@সামিন সালেক – You need to read up about complex analysis and contour integration. There are Wikipedia articles on both of these. You could start there. There is a Brilliant wiki on contour integration as well, but it does not go very far.
@সামিন সালেক – After the substitution is done, you need Cauchy’s Residue Theorem.
I'm a bit confused: the area of the blue circle is 20×Pi and the area of the eclipse (inside of the blue circle) is 39×Pi?
Sorry, confused area with length...
Btw what is this
Log in to reply
This is what's called a Steiner's chain - draw a series of circles tangent to both the blue and red circles, where each one in the series is also tangent to the last. The spacing of the series is such that you get a lot of circles, and thus a lot of circle centers, before the last circle in the series winds up being tangent to the first.
Fun fact, Steiner's porism is a theorem that states that if any series of circles connects so that the last one is tangent to the first, then all such series will.
Let the above diagram represent one of the positions of the black circle. Let the radius (at the instant) of the black circle be B D = r , where B is the centre of the black circle. Let A and C denote the centres of the red and blue circles respectively. From the diagram, we see that
A B = A E + E B = 3 + r B C = C D − B D = 1 0 − r
We find that A B + B C = 1 3 is a constant. Hence the locus of B is an ellipse with major axis length 2 a = 1 3 , i.e., length of semi-major axis a = 2 1 3 .
The points A and C are the focii of the ellipse and the distance between them is 2 a e = 5 , where e denotes the eccentricity of the ellipse. From the values given above we get e = 1 3 5 .
Using the identity b 2 = a 2 ( 1 − e 2 ) , we get b = 6 , where b is the length of semi-minor axis of the ellipse.
The area of the ellipse gives the required area of the closed curve given by A = π a b = π ⋅ 2 1 3 ⋅ 6 = 3 9 π . The answer is thus 3 9 .