Gold and Silver Coins
 You randomly choose a treasure chest to open, and then randomly choose a coin from that treasure chest. If the coin you choose is gold, then what is the probability that you chose chest A?
You randomly choose a treasure chest to open, and then randomly choose a coin from that treasure chest. If the coin you choose is gold, then what is the probability that you chose chest A?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
I don't agree. If You label one chest A and the other B, then hide those labels and let someone choose one chest. the probability it would be A is halve.
Log in to reply
The question is not "what is the probability of choosing chest A?" but "what is the probability that the gold coin you have came from chest A?"
Log in to reply
Read the qn. It says the probability of choosing chest A.
Log in to reply
@Zhi Wei – "If the coin you choose is gold, then what is the probability that you chose chest A?"
or
Given that you chose a gold coin, what is the probability that you chose chest A?
or
Probability of chest A, given that you chose a Gold coin?
therefore
P(A|G) = the most accurate representation of the question asked.
Log in to reply
@Brian Egedy – Interesting, I also read "chose" as "choose", which produced the same confusion. As usual, words are harder than mathematical expressions. The sequence of actions is expressed easier in a math expression. Obviously.
the question is "what is the probability that you chose chest A" and not "what is the probability that the gold coin you have came from chest A". The question is misleading
Log in to reply
I do agree with da answer given. The question isnt misleading.
If you had taken a silver coin instead of a golden one, would you still think that the probability of having chosen chest A is 50%? Baye's theorem is sometimes counterintuitive (as can be probability itself), and that could also be called misleading...
I understood the concept and got the answer correctly but it says incorrect. 🤣
Why do I get "incorrect" when I selected 2/3?
Damn this is confusing
the question is about the chest not the coin " If the coin you choose is gold, then what is the probability that you chose chest A"? The question did not put emphasis on the probability of the coin.
The question did not ask "what is the probability that the coin would be gold"?
I chose 2/3. The response was "Incorrect". If the intention was to lead me here to explore the various explanations and comments, then it's ok.
I kind of guessed 2/3 knowing 1 is a 100% chance and the other is 50% but when i put this into my calculator I get 1.25 (0.5 1)/(0.5 1)+(0.5*0.5) Am I just making a rookie error in input?
@Chris Spencer you've got the parenthesis wrong in your calculation, it should be (0.5)/(0.5 + 0.5*0.5)
Aristo style, pure logic solution, no formula necessary: Let's breakdown all possible outcomes: Either we choose chest A or B, and then we choose gold or silver..; so; 1- A -> gold (100 events) 2-B -> gold (50 events) 3-B -> silver(50 events)
So because we ARE TOLD, we DO KNOW, that we have a gold coin in hand , so - our event space narrows down to first two event groups: (1+2) ...which means we have MAX.(100+50=150events) and in those 150 events, the qty of options which includes chest A as an event is only and completely row 1...which is 100 events
so possibility of choosing ( or coming across chest A amongst all possibilities ) is : 100events/(100+50)events = 2/3
That explanation helped me understand completely. Thank you.
Log in to reply
I guessed 2/3 and it says I'm incorrect. I don't get it
how did u get 200/300?
now it is clear, thanks you .
When we choose randomly a gold coin, from two boxes of 100 gold, 50 gold and 50 silver, total out come is 3 and favourable out come is two. Therefore Probabilit of getting gold coin is 2/3.
There are 150 gold coins in both chests combined. Chest A has twice as many as Chest B. Knowing that you chose a gold coin, look at your entire universe of possibilities as 150 coins. 100 of those lie in Chest A (100/150), making the probability that you chose from Chest A: 2/3.
The probability of getting a gold coin in chess A is 1/2. The probability of getting a gold coin in chess B is 1/2 x 1/2 = 1/4. If the coin you choose is gold, the probability that you chose chest A = 1/2 / (1/2 + 1/4) = 2/3
We need to find P(A|G)-ie the probability of picking up from A given evidence is -it is a Gold coin. P(G|A): prob of gold if chest is A=1. P(A): P(A)=P(B)=0.5. P(G)=150/200 =3/4. From Bayes P(A/G)=P(G/A) * P(A)/P(G)= 1 * 0.5 * 4/3= 2/3
This simple explanation made the magic for me. ^..^
P(H) = 0.5 P(E) = 3/4
P(E/H) = 1
applying baye's formula 2/3
Probability to extract gold in total is P(gold)=150/200 = 3/4; Probability to open chest A is P(A) = 1/2 that's the prior ; probability to extract gold form chest A is P(gold|A) = 1; Plugging in together in the formula: P(A|gold)=(P(gold|A)/P(gold)) P(A) = (1/(1/2)) 3/4=2/3
There are 150 gold coins. 100 are in Chest 1. 50 are in Chest 2. The probability the gold coin comes from chest 1 is 100/150 or 2/3.
Both are same
This method seems simpler.
Yayyy, i got right :D lol well I'm just trying to put my understanding in consideration from the Bayes Theorem {may not be accurate explanation}
Probability of choosing the Treasure A out of Two Treasures is 1/2 aka Prior Probability
Probability of Choosing the Gold Coin out of total available coins is 150 / 200 = 3/4
Probability of Choosing the Gold Coin exclusively from the Treasure A is 100/100 = 1 {It is so obvious that there are cent percent chances}
Probability for choosing the Treasure A given the evidence that the coin is Gold = Prior Probability Times likelihood ratio = (1 / 2) * ( 1 / (3/4)) = (1/2) * (4/3) = 2/3
X -- Chance to Select chest A Y -- Chance to select Gold coin Need to find p(X|Y) ? p(X|Y) = (p(X) p(Y|X))/p(Y) p(X) = 1/2 , p(Y) = 150/200 = 3/4 , p(Y|X)=1 p(X|Y) =(1/2 1)/3/4 = 2/3
- Using a more intuitive approach, in chest A there are 100 gold coins and in chest B there are 50 gold coins so the ratio of gold coins A : B = 2 : 1, hence the probability a person chooses A from a (virtual) chest that contains both A and B is 2 / (2 + 1) = 2/3
Known : - P(A) - probability of selecting chest A = 1/2, - P(G) - probability of selecting gold coin = 150/200 = 3/4, - P(G|A) - probability that the coin is gold given you selected from chest A = 1 (as all the coins are gold in chest A),
To find : P(A|G) - probability that the coin is from chest A given the coin is a gold coin, P(A|G) = P ( G ) P ( G ∣ A ) . P ( A ) = 3 2
P(A|G) = P(G|A) * P(A) / P(G) = 1 * (1/2) / (3/4) = 2/3
reduce the sample since we know that the coin is gold and then the expression becomes 100/150 which is 2/3
p(a/gold)=p(a) p(gold/a) / p(gold) =2/3
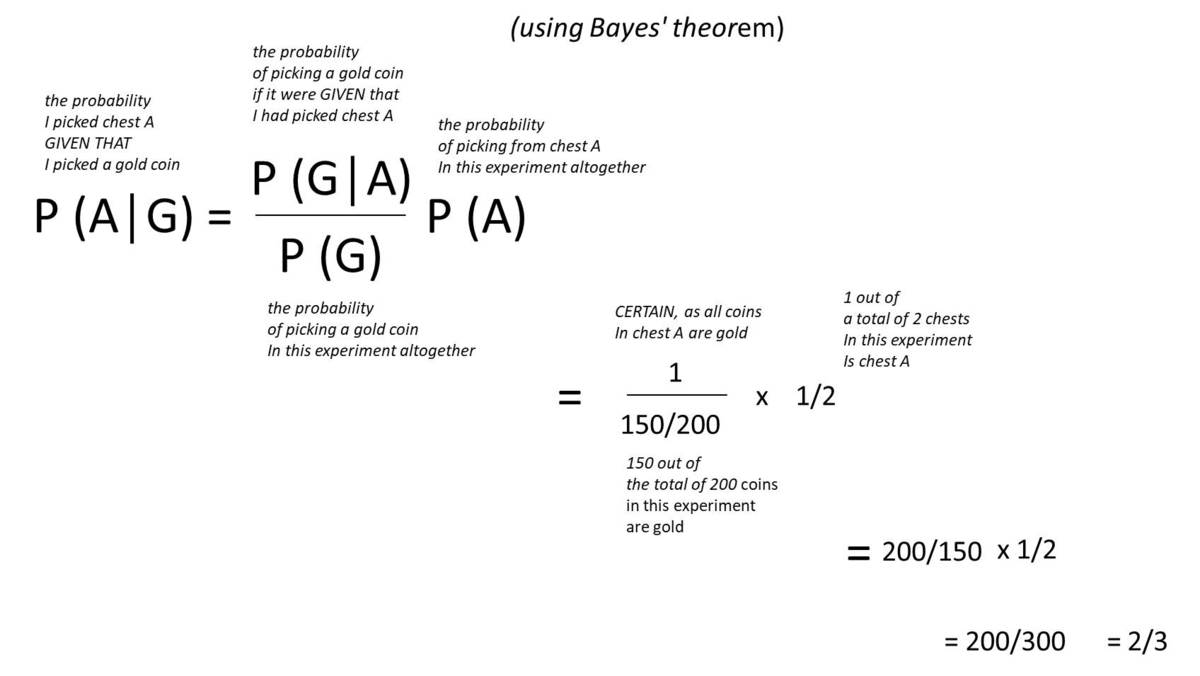
Intuitive Explanation: There are two ways to get a gold coin: from chest A (from which we have 100% chance), or from chest B (from which we have 50% chance). Since we are twice as likely to get a gold coin if we are choosing from chest A, the odds that we chose from chest A are 2 : 1 , so the probability is 3 2 .
Formal Explanation: We can apply Bayes' Theorem to this problem. Let G be the event of selecting a gold coin, and note that P ( G ∣ A ) = 1 and P ( G ∣ B ) = 2 1 . Via Bayes' Theorem, P ( A ∣ G ) = P ( G ) P ( A ) ⋅ P ( G ∣ A ) = P ( A ) ⋅ P ( G ∣ A ) + P ( B ) ⋅ P ( G ∣ B ) P ( A ) ⋅ P ( G ∣ A ) = 2 1 ⋅ 1 + 2 1 ⋅ 2 1 2 1 ⋅ 1 = 3 2 .