Golden Problem!

Geometry Level 3

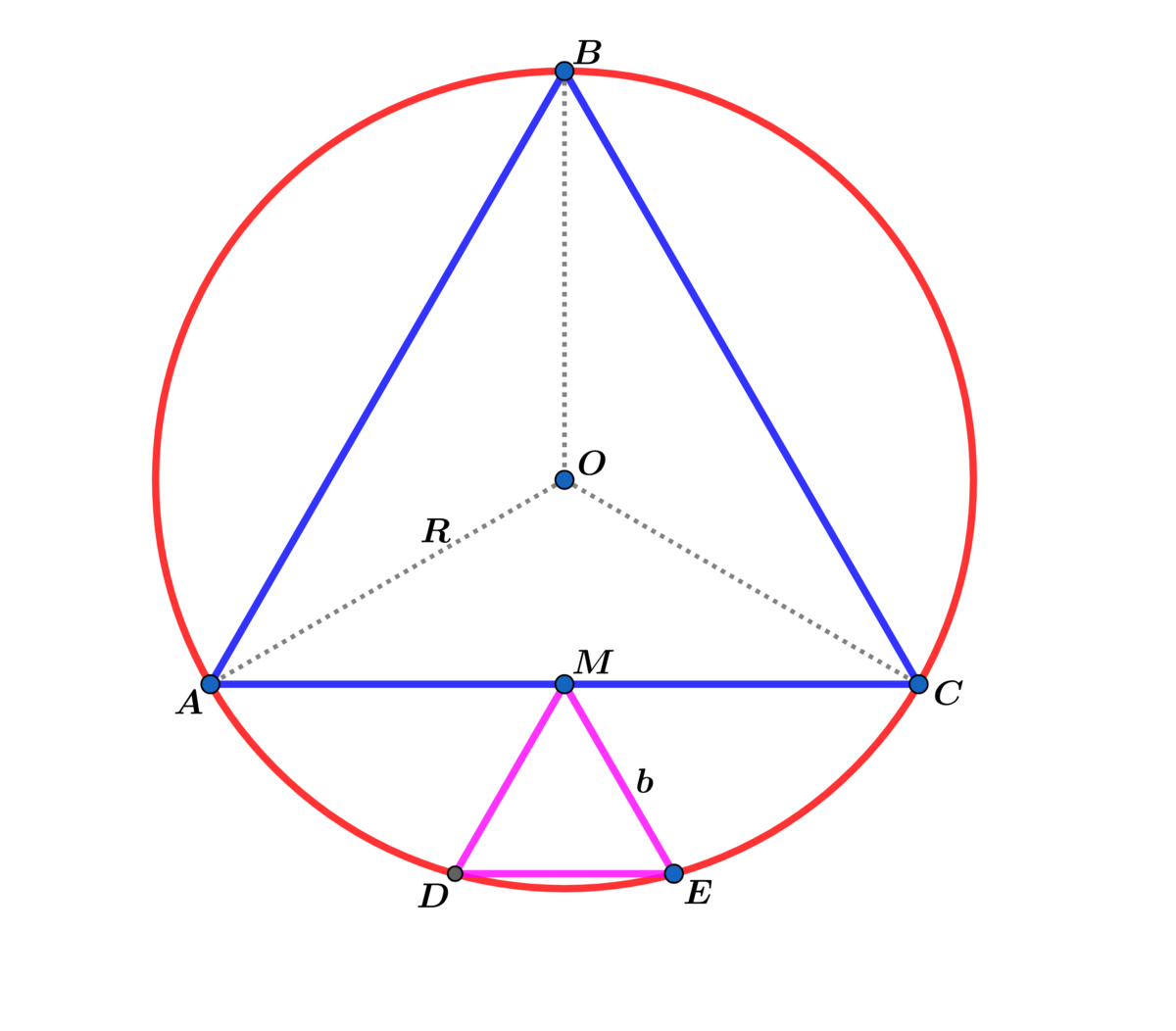
Equilateral $\triangle{ABC}$ is inscribed In the circle above with radius $R$ and Equilateral $\triangle{DME}$ with side length $b$ has vertex $M$ at the midpoint of $\overline{AC}$ and the other two vertices $D$ and $E$ are on the circle.

If $\dfrac{b}{R} = \dfrac{\sqrt{\alpha}}{\beta}(\phi - 1)$ , where $\phi$ is the golden ratio and $a$ and $b$ are coprime positive integers, find $\alpha + \beta$ .

The answer is 5.

2 solutions

Rocco Dalto
Mar 19, 2021

$h = \dfrac{R}{2}$ and $h^{*} = \dfrac{\sqrt{3}}{2}b \implies h + h^{*} = \overline{ON} = \dfrac{\sqrt{3}}{2} + \dfrac{R}{2}$ .

Using Pythagorean Theorem on right $\triangle{ODN} \implies (\dfrac{\sqrt{3}}{2}b + \dfrac{R}{2})^2 + \dfrac{b^2}{4} = R^2 \implies$

$(\sqrt{3}b + R)^2 + b^2 = 4R^2 \implies 3b^2 + 2\sqrt{3}bR + R^2 + b^2 = 4R^2 \implies$

$4b^2 + 2\sqrt{3}R - 3R^2 = 0 \implies b = \dfrac{\sqrt{15} - \sqrt{3}}{4}R$ dropping the negative root

$\implies \dfrac{b}{R} = \dfrac{\sqrt{3}}{2}(\dfrac{\sqrt{5} - 1}{2}) = \dfrac{\sqrt{3}}{2} (\phi - 1) =$ $\dfrac{\sqrt{\alpha}}{\beta}(\phi - 1) \implies \alpha + \beta = \boxed{5}$ .

Do you need to specify that the triangles are equilateral for this problem, rather than isosceles?

Dan Brabec - 2 months, 3 weeks ago

Yes. In my solution I used the fact the both triangles are equilateral. I used this fact below:

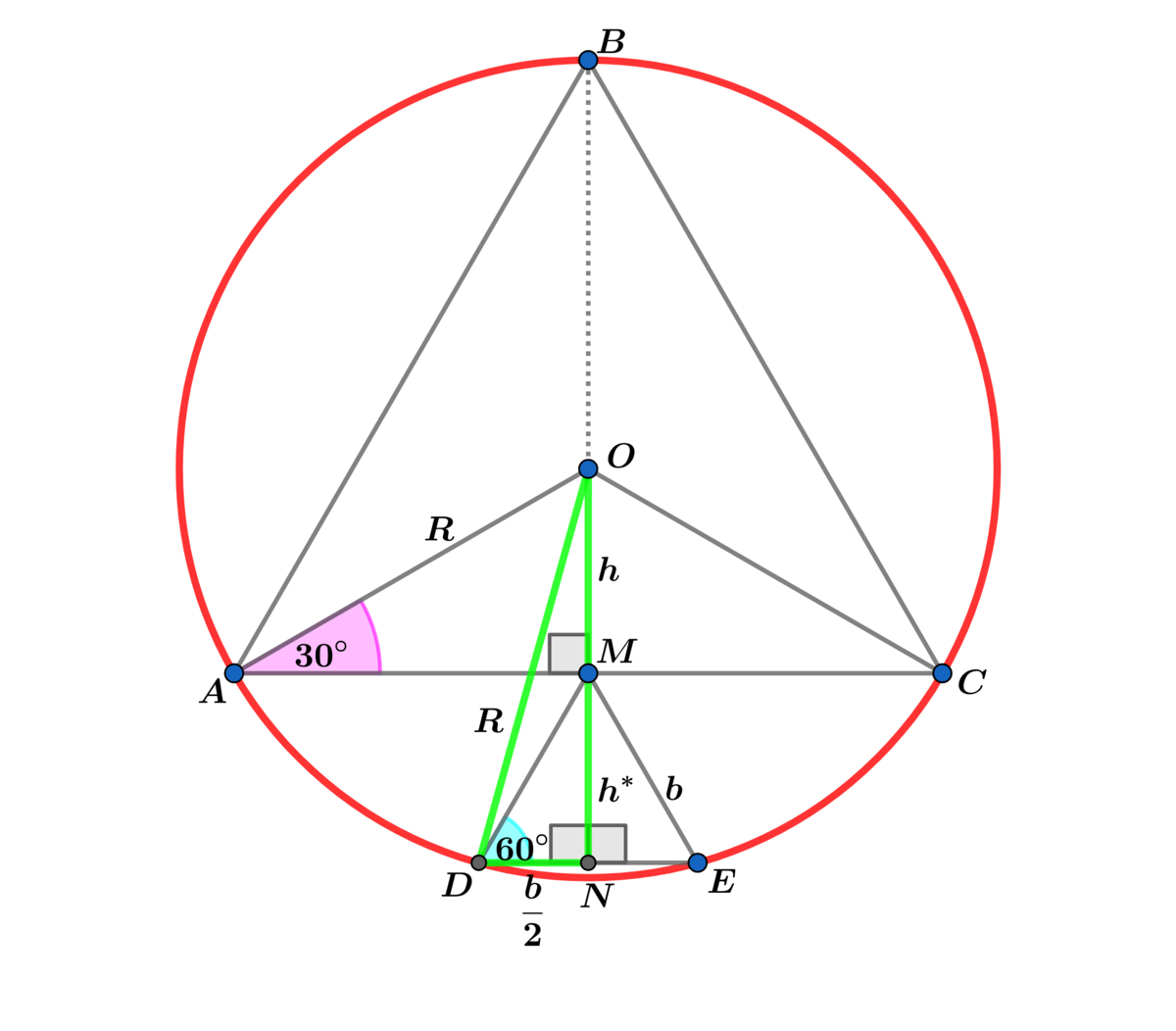
In $\triangle{ABC} \:\ h = R\sin(30^{\circ}) = \dfrac{R}{2}$ and in $\triangle{DME} \:\ h^{*} = R\sin(60^{\circ}) = \dfrac{\sqrt{3}}{2}b$

Rocco Dalto - 2 months, 3 weeks ago

I saw that, but the original problem states that the two triangles are isosceles which means your solution represents only one specific situation where the isosceles triangles are actually equilateral. If both triangles were isosceles right triangles, for example, the ratio of b/R would actually be 1. I think that you need to clarify that in how you state the original problem.

Dan Brabec - 2 months, 3 weeks ago

@Dan Brabec – I thought I typed Equilateral. I changed it. Thanks!

Rocco Dalto - 2 months, 3 weeks ago

I think it is worth mentioning what Fukagawa Hidetoshi and Tony Rothman tell us about this problem in their valuable book SACRED MATHEMATICS: Japanese Temple Geometry (problem 6, page 95):

"We know of this problem from the unpublished manuscript Jinbyo Bukkaku Sangakushu , or Collection of Sangaku from the Aida School, written by Aida Yasuaki (1747–1817) at an unknown date. The problem was originally proposed in 1800 by Kobata Atsukuni, a student of the Aida school, and presented on a tablet to the Kanzeondo temple of Toba castle town."

Thanos Petropoulos - 2 months, 3 weeks ago

I don't know of the book, but this is a Japanese Temple Problem.

Rocco Dalto - 2 months, 3 weeks ago

Check it out. It is a very interesting reference book for Japanese temple geometry.

Thanos Petropoulos - 2 months, 3 weeks ago

@Thanos Petropoulos – I'll check it out. Thanks!

Rocco Dalto - 2 months, 3 weeks ago

David Vreken
Mar 19, 2021

Let $R = 1$ and draw $OM$ and $OE$ . Then $OE = OA = R = 1$ , and by the properties of an equilateral triangle, $OM = \frac{1}{2}OA = \frac{1}{2}R = \frac{1}{2}$ .

Also, $\angle OME = \angle OMC + \angle CME = 90° + 60° = 150°$ .

By the law of cosines on $\triangle OME$ , $\cos \angle OME = \cfrac{OM^2 + ME^2 - OE^2}{2 \cdot OM \cdot ME}$ , or $\cos 150° = \cfrac{(\frac{1}{2})^2 + b^2 - 1^2}{2 \cdot \frac{1}{2} \cdot b}$ , which solves to $b = \sqrt{3}\bigg(\cfrac{\sqrt{5} - 1}{4}\bigg) = \cfrac{\sqrt{3}}{2}(\phi - 1)$ .

Therefore, $\alpha = 3$ , $\beta = 2$ , and $\alpha + \beta = \boxed{5}$ .

Golden Problem!

The answer is 5.

2 solutions

0 pending reports