Good analytical geometry from

Geometry Level 5

In the figure below,

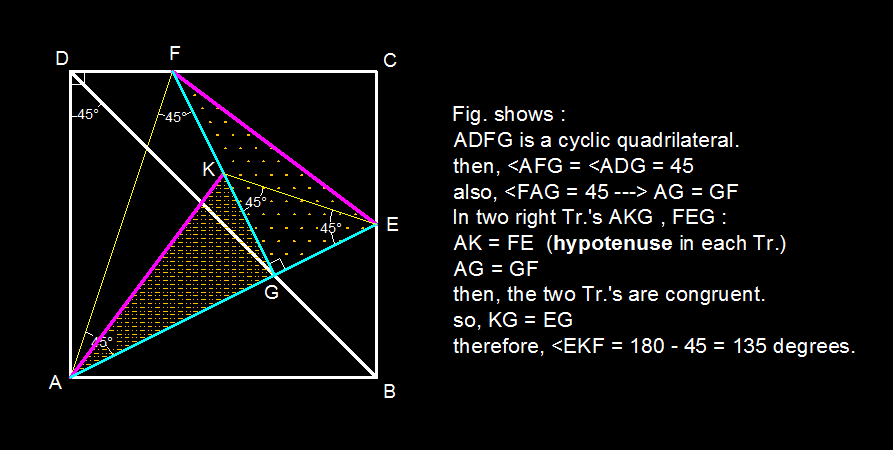
$ABCD$ is a square. $E$ and $F$ are points on $BC$ and $CD$ respectively such that $AE$ cuts the diagonal $BD$ at $G$ and $FG$ is perpendicular to $AE$ . $K$ is a point on $FG$ such that $AK = EF$ . Find the measure of angle $EKF$ in degrees.

The answer is 135.

3 solutions

Ahmad Saad
Jan 23, 2016

Priyanshu Mishra
Jan 18, 2016

Since $\angle AGF = 90^o$ and $\angle ADF = 90^o$ , it follows that $ADFG$ is a cyclic quadrilateral. Hence $\angle GAF = \angle GDF = 45^o$ . Thus the triangle $AGF$ is isosceles and $AG = GF$ . In the right angled triangles $AGK$ and $FGE$ , we have $AK = EF$ and $AG = GF$ . Hence they are congruent and $GE = KG$ . Consequently, the right angle triangle $KGE$ is isosceles and $\angle EKG = 45^o$ . Thus

$\angle EKF = 180^o - \angle EKG = \boxed{135^o}$

I think you have to prove congruency.

Niranjan Khanderia - 5 years, 4 months ago

I think the main part of the solution should be the proof that the triangles are congruent.

Anupam Nayak - 5 years, 4 months ago

The proof is left to the reader.

Also I did same thing to prove congruency as done by Ahmad Saad.

Priyanshu Mishra - 5 years, 4 months ago

If the proof is left to the reader, what's the point of even writing a solution. You didn't even give an outline of your proof that those two triangles are congruent.

Anupam Nayak - 5 years, 4 months ago

@Anupam Nayak – Ok. I am sorry for NOT RIGHTING THE COMPLETE SOLUTION. I have edited it.

Also don't be so rude and force me to write the solution of my own problem. It's my choice whether to write the solution or not. If you are the top ranker of RMO, INMO, IMO, AIME, USAMO : then why don't you post the solution? Neither you are the staff of BRILLIANT nor are you the moderator who can force me to post the solution. So, please mind your language.

You can downvote my solution, if you want. I will not say anything, but you cannot force me rudely to post the COMPLETE SOLUTION .

Priyanshu Mishra - 5 years, 4 months ago

@Priyanshu Mishra – I'm sorry if that sounded rude. I was not forcing you to write the complete solution, I was just trying to help you make the solution better. I'm sorry again.

Anupam Nayak - 5 years, 4 months ago

@Anupam Nayak – If this was your intention, then no problem.

Thanks for forcing me. lol, I became active after that in writing complete solutions. : )

Priyanshu Mishra - 5 years, 4 months ago

Hey brother, how will you price the congurency.

Department 8 - 5 years, 4 months ago

The proof is same as that of Ahmad.

Also I felt lazy to type the congruency proof , so I left it.

Priyanshu Mishra - 5 years, 4 months ago

Lol, you on Slack? I want to talk to you.

Department 8 - 5 years, 4 months ago

@Department 8 – What is slack?

I just opened it once but not knew that i had been added.

Can you tell me how to go on 'SLACK CHAT''? What is the url?

Priyanshu Mishra - 5 years, 4 months ago

@Priyanshu Mishra – Go to brilliant-lounge.slack.com and sign up. If this does not work then ask Calvin sir.

Department 8 - 5 years, 4 months ago

@Department 8 – I have been welcomed to on slack chat.

Now how to chat with you?

Priyanshu Mishra - 5 years, 4 months ago

Des O Carroll
Jan 21, 2016

using coordinate geometry and letting e be(1,t) then g is (1/1+t,t/1+t) f is(1-t/1+t,1) ok=fe =(t^2+1)/t+1 which gives kg which we find=ge

Moderator note:

Since it's a proof by coordinate geometry, you would have to provide all of the values that you calculated, instead of just saying "gives kg which we find = ge".

Thanks for the brief solution.

Priyanshu Mishra - 5 years, 4 months ago

Good analytical geometry from

The answer is 135.

3 solutions

Moderator note:

0 pending reports